Chapter 3: Angular Momentum
0.0(0)
0.0(0)
Card Sorting
1/42
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
43 Terms
1
New cards

Orbital Angular Momentum Operator
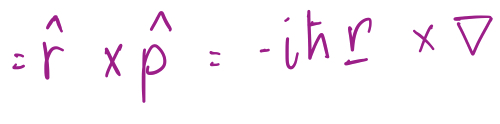
2
New cards
Laplacian in spherical polar coordinates
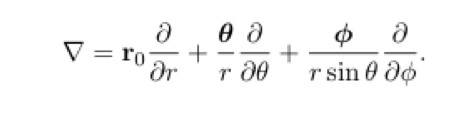
3
New cards

Orbital Angular Momentum Operator in spherical coordinates
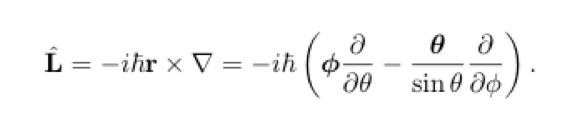
4
New cards
Spherical polar coordinates
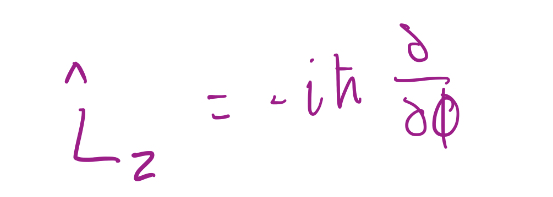
5
New cards
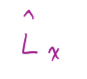
Spherical polar coordinates
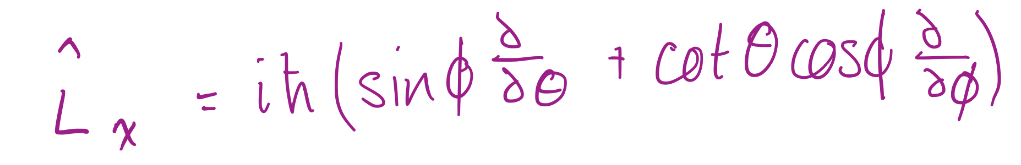
6
New cards

Spherical polar coordinates
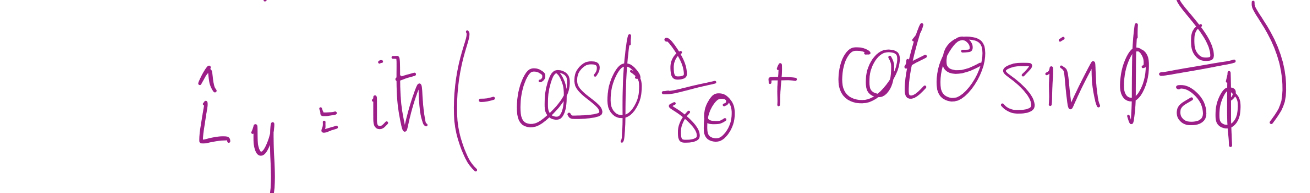
7
New cards

Spherical polar coordinates
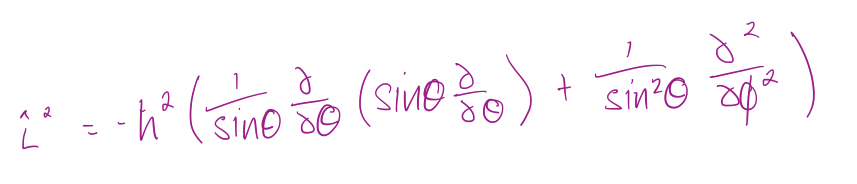
8
New cards
Eigenvalues and eigenfunctions are given by
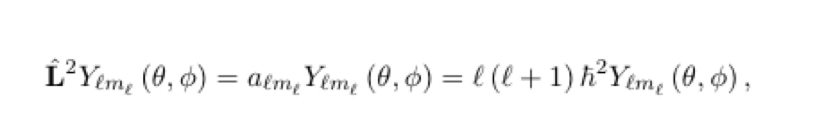
9
New cards
z-component is given by
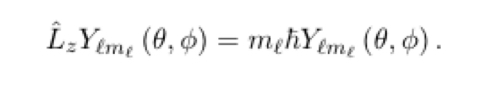
10
New cards
Both L^2 and L^z assume
one set of discrete values
11
New cards
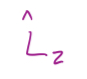
In terms of p^ and r^
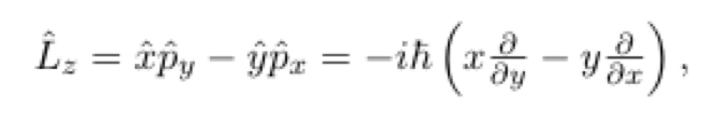
12
New cards
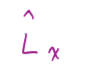
In terms of p^ and r^
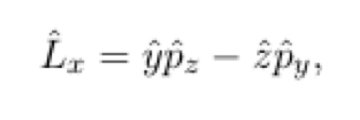
13
New cards

In terms of p^ and r^
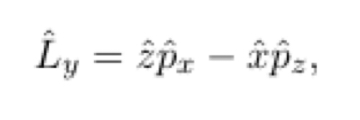
14
New cards
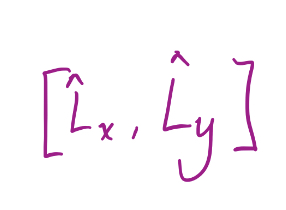
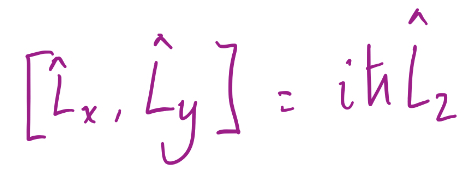
15
New cards
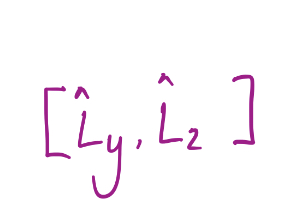
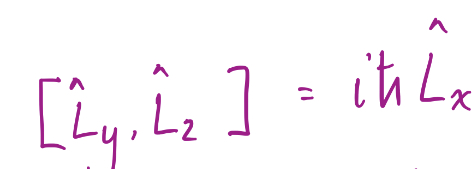
16
New cards
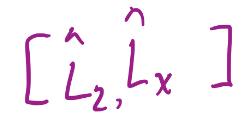
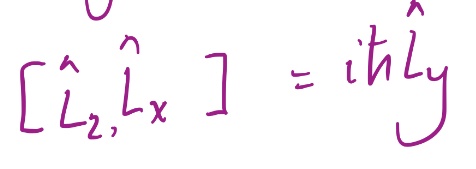
17
New cards
L^2 commutes with
L^x, L^y, and L^z and L^+ and L^-
18
New cards
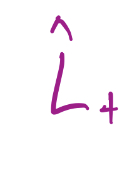
Raising Operator
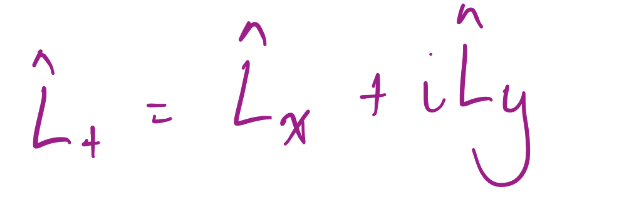
19
New cards
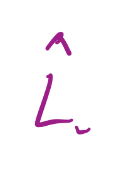
Lowering Operator
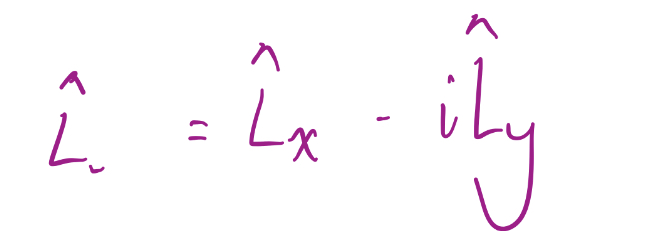
20
New cards
Raising and lowering operators are not
Hermitian
21
New cards
Raising and lowering operators do not
represent physical quantities
22
New cards
Raising and lowering operators do
raise the eigenfunctions of L^z up or down the “ladder” of eigenvalues L^z
23
New cards
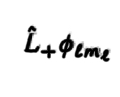
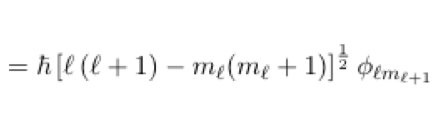
24
New cards
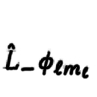
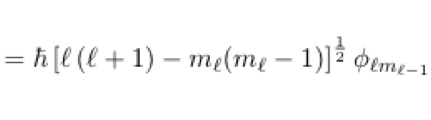
25
New cards
What is the effective current, i, for a particle with charge e-, mass me, moving in an orbit at a radius of a0 at an angular velocity ω?
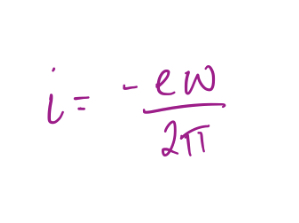
26
New cards
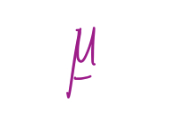
Magnetic moment associated with effective current, i, for a particle with charge e-, mass me, moving in an orbit at a radius of a0 at an angular velocity ω

27
New cards
Orbital angular momentum, **L**

28
New cards
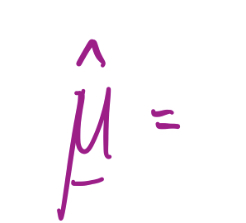
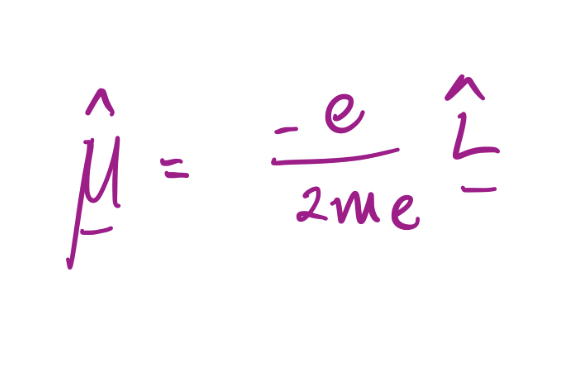
29
New cards
gyromagnetic ratio
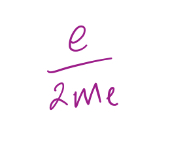
30
New cards
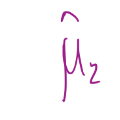
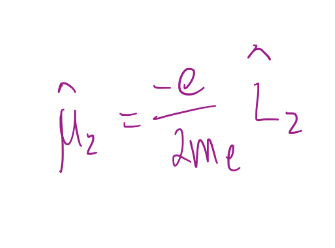
31
New cards

Bohr magneton
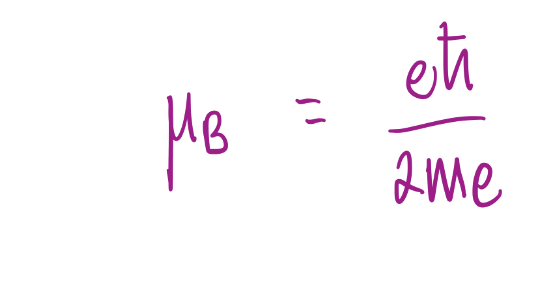
32
New cards
What happens when you apply a **B** field?
The energy levels split by ΔE
33
New cards
ΔE
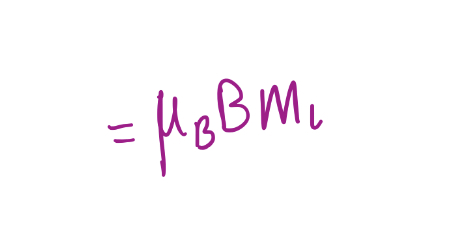
34
New cards
What did Stern Gerlach experiment find?
* An atom’s orbital angular momentum is quantised
* some particles possess an intrinsic angular momentum, called spin
* some particles possess an intrinsic angular momentum, called spin
35
New cards
What is spin, S?
Intrinsic angular momentum, possessed by some particles (e.g. electrons, protons, neutrons)
36
New cards
What are the spin quantum numbers for an electron?
s = 1/2
ms = +/- 1/2
ms = +/- 1/2
37
New cards
Does orbital angular momentum require that there is an odd or even number of eigenstates of L^z?
Odd → 2l+1
38
New cards
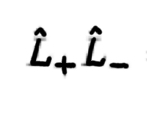
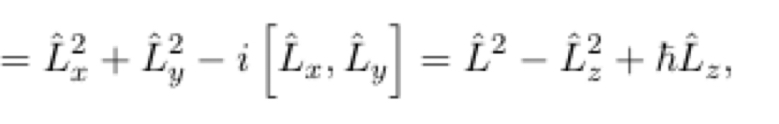
39
New cards
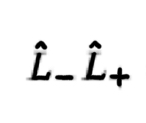
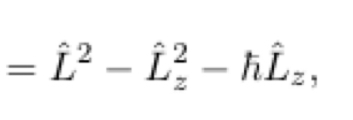
40
New cards
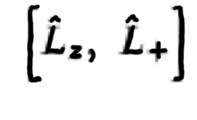
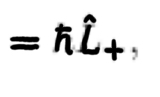
41
New cards
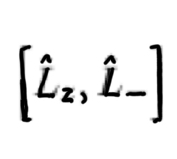
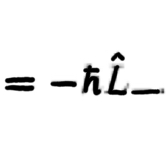
42
New cards
**Orbital** angular momentum has an extra (?) condition that the wave function must be a well behaved function of position. What does this require?
n must be even and so l must have an integer value
43
New cards
Does an electron spin?
No but it has intrinsic angular momentum which is called spin