1.03-1.10 Average Speed, Velocity, & Acceleration
0.0(0)
0.0(0)
Card Sorting
1/42
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
43 Terms
1
New cards
Distance-time graphs
Graphs which show how the distance (y-axis) of an object varies over time (x-axis).
2
New cards
Slope of distance-time graphs
Slope of distance time graphs = 𝚫y/𝚫x = 𝚫 distance/𝚫 time = speed of object
3
New cards
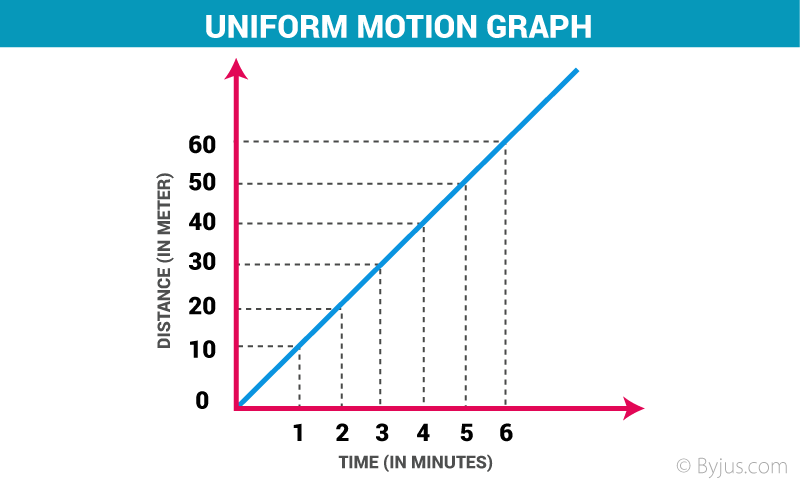
Straight, linear slope (gradient) for distance-time graphs
Straight, linear slope (gradient) → constant speed
4
New cards
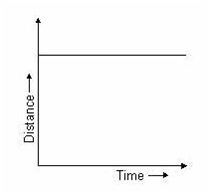
Horizontal slope (gradient) for distance-time graphs
Horizontal slope (gradient) → 𝚫y/𝚫x = 0/𝚫x = 0/𝚫 time = 0 → stationary (not moving) object
5
New cards
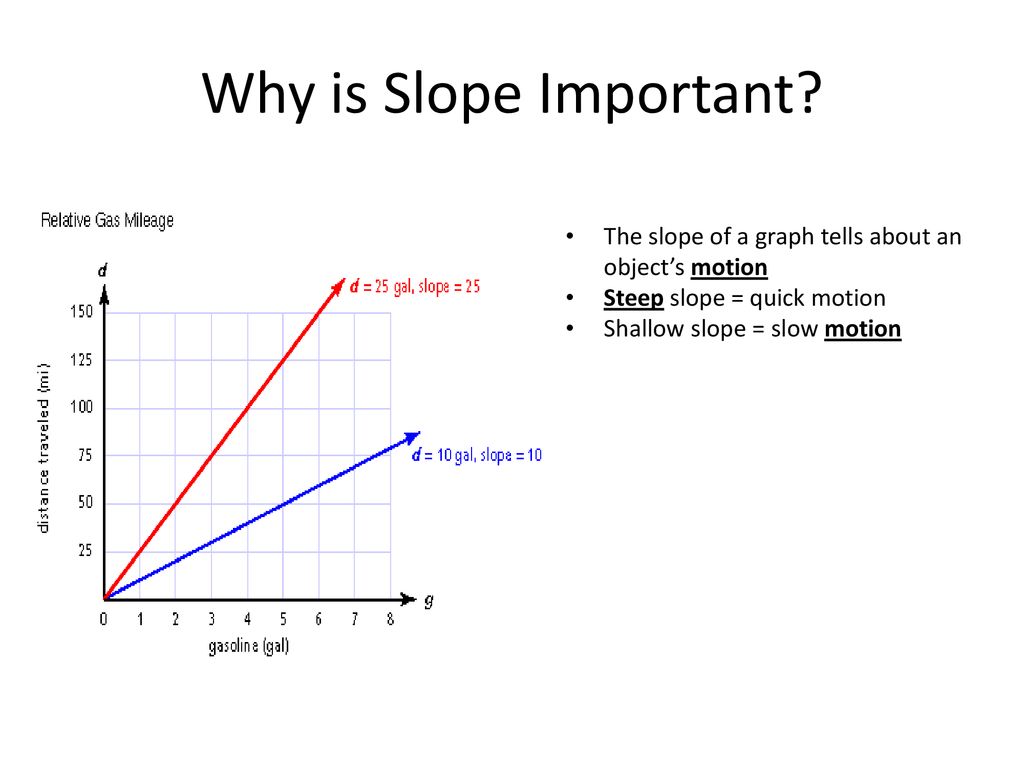
Steep slope (gradient) for distance-time graphs
Steep slope (gradient) → ↑ 𝚫y over 𝚫x → ↑ 𝚫 distance over 𝚫 time → ↑ speed
6
New cards
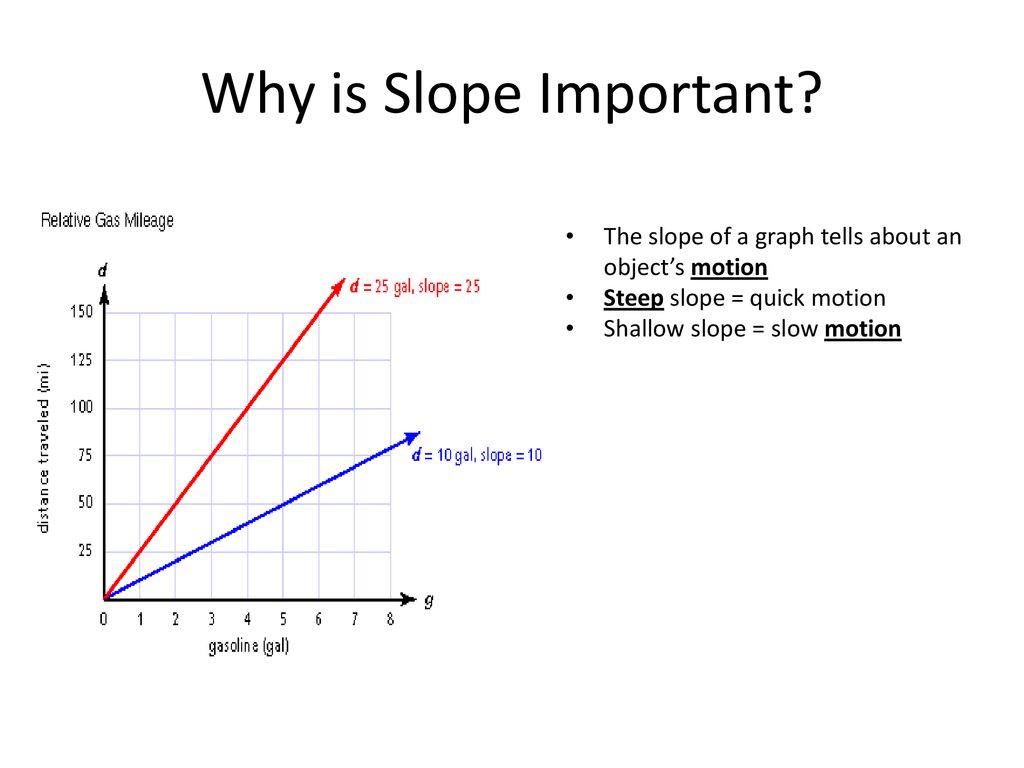
Shallow (gentle) slope (gradient) for distance-time graphs
Shallow slope (gradient) → ↓ 𝚫y over 𝚫x → ↓ 𝚫 distance over 𝚫 time → ↓ speed
7
New cards
Curved line in distance-time graph
Curved line → changing velocity or speed
8
New cards
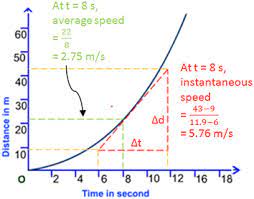
How do you find the instantaneous speed at a point on a distance-time graph?
If the point of instantaneous speed is on a linear segment of the graph, then the speed is simply the gradient of that linear segment. If the point of instantaneous speed is on a non-linear/curved section of the graph, then draw a line tangent to that point on the curve, then find the tangent’s gradient. Tangent’s gradient = Object’s speed at that instantaneous moment in time. This method also works for finding instantaneous acceleration in velocity-time graphs.
9
New cards
Gradient becomes steeper in curved line on distance-time graph
Gradient becomes steeper → acceleration
10
New cards
Gradient becomes shallower in curved line on distance-time graph
Gradient becomes shallower → deceleration

11
New cards
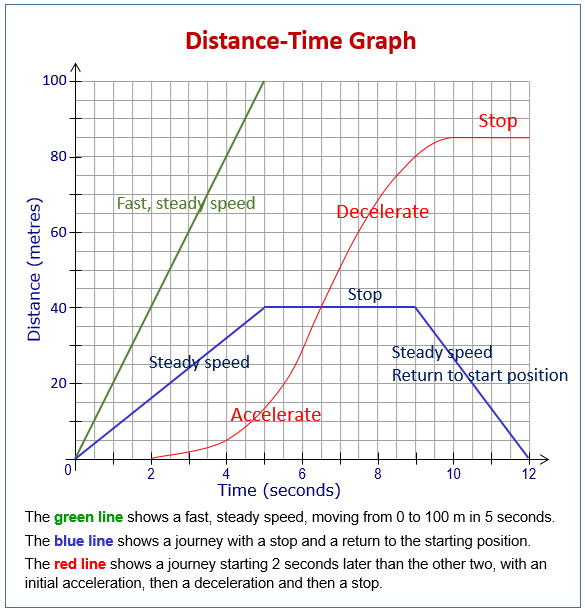
Distance = 0 on distance-time graph
Distance = 0 → Back at starting point
12
New cards
Negative slope (gradient) on distance time graph
Negative slope → Distance between object and starting point is decreasing → Object is traveling in opposite direction and is going back to the starting point (e.g. if object was previously traveling west, then a negative slope indicates that it is now traveling east)

13
New cards
Average speed definition
Total distance travelled by an object in a particular time interval. It’s a scalar quantity (because it only has magnitude and no direction).
14
New cards
If an object’s average speed or average velocity changes over time, what does this indicate?
Indicates acceleration has occurred.
15
New cards
Average speed formula
Average speed = Distance travelled / Time taken
16
New cards
Distance travelled formula
Distance travelled = Average speed x Time taken
17
New cards
Time taken formula
Time taken = Distance travelled / Average speed
18
New cards
Distance
How much ground an object has covered or travelled across during its motion. It’s the length of the space between 2 points (for physics, these 2 points would be the starting and ending point of the object). Distance is a scalar quantity, it has no regards to direction.
19
New cards
Displacement
Distance travelled in a particular direction from a specified point. Displacement is a vector quantity.
20
New cards
Distance VS displacement
Distance is scalar, displacement is vector.
21
New cards
Average velocity formula
Average velocity = Change in displacement / time taken
22
New cards
Average speed VS Average velocity
Average speed is scalar, average velocity is vector
23
New cards
Fiducial mark
Point of reference, where the same point is used when measuring.
24
New cards
What methods can you use to investigate the speed of an object?
1. Use trolley/ramp:
1. Heavy trolley/object used → put buffer material at end of runway (point B).
2. Heavy wooden ramp used → use at low level near floor rather than on benches or tables where it can fall off.
3. Measure AB’s length (distance trolley travels).
4. Use stopwatch to measure trolley’s time taken to travel across AB; human reaction time → error.
5. Calculate average speed using formula.
6. Always measure point A → constant distance AB
7. Change h to see height of ramp’s effect on trolley’s average speed.
8. Ignore anomalous results when calculating averages.
2. Use stroboscope in dark room to light up object at regular, known intervals (found from stroboscope’s frequency setting) with the camera adjusted so the shutter is open for the duration of the movement.
3. Use video camera to find distance object travelled between each frame - frame rate allows you to calculate time between each image/frame.
4. Use light gates. Using electronic timing devices has an advantage of removing timing errors produced from/by human reaction time.
25
New cards
Stroboscope
Apparatus that produces short bright flashes of light at regular intervals (at a known frequency of flashes per second); the apparatus allows the frequency to be varied. Stroboscopes are used to allow a series of images of a moving object to be captured photographically or to determine the speed of rotating objects.
26
New cards
Light gate
Apparatus used to measure speed. It has 2 pairs of infrared transmitters and receivers that will detect an object passing through. Average speed can be calculated as (known distance between 2 pairs of sensors) / (time taken to pass through light gate). Acceleration can also be calculated by measuring the average speed, as well as the time taken to go from resting state to traveling at the average speed (or measure differences in velocity using 2 light gates, then divide this difference by the time to get acceleration or deceleration).
27
New cards
Acceleration definition
Change in velocity (m/s) per unit time (s) → units of ㎨.
28
New cards
Acceleration formula
Acceleration = Change in velocity / time taken
a = (v-u)/t
a = (v-u)/t
29
New cards
Deceleration definition
Reduction in average velocity/speed or increase in velocity/speed in the opposite direction (hence the - sign).
30
New cards
Velocity time graphs
Graphs which show how the velocity (y-axis) of an object varies over time (x-axis).
31
New cards
Slope of velocity-time graphs
Slope = 𝚫y/𝚫x = 𝚫 velocity / 𝚫 time = acceleration of object
32
New cards
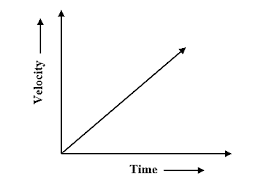
Straight, linear slope (gradient) for velocity-time graphs
Straight, linear slope (gradient) → constant acceleration
33
New cards
Horizontal slope (gradient) for velocity-time graphs
Horizontal slope (gradient) → 𝚫y/𝚫x = 0/𝚫 time = 0 → No 𝚫velocity → no acceleration or deceleration → constant speed
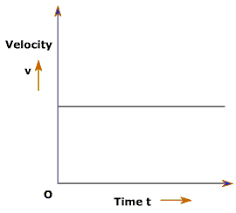
34
New cards
Steep slope (gradient) for velocity-time graphs
Steep slope (gradient) → ↑ 𝚫y over 𝚫x → ↑ 𝚫 velocity over 𝚫 time → ↑ acceleration
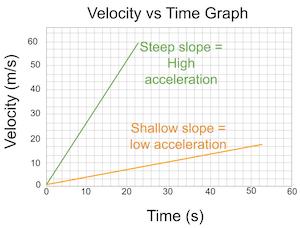
35
New cards
Shallow (gentle) slope (gradient) for velocity-time graphs
Shallow slope (gradient) → ↓ 𝚫y over 𝚫x → ↓ 𝚫 velocity over 𝚫 time → ↓ acceleration
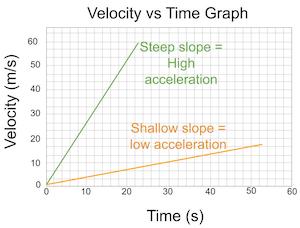
36
New cards
Curved line in velocity-time graph
Curved line → changing acceleration or deceleration
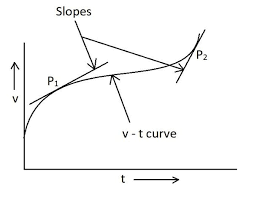
37
New cards
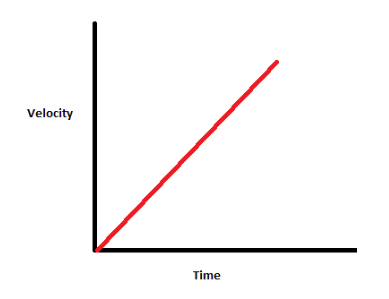
Positive gradient in velocity-time graph
Positive gradient → acceleration
38
New cards
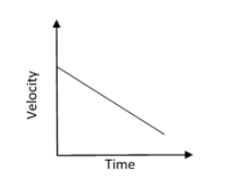
Negative gradient in velocity-time graph
Negative gradient → negative acceleration → deceleration
39
New cards
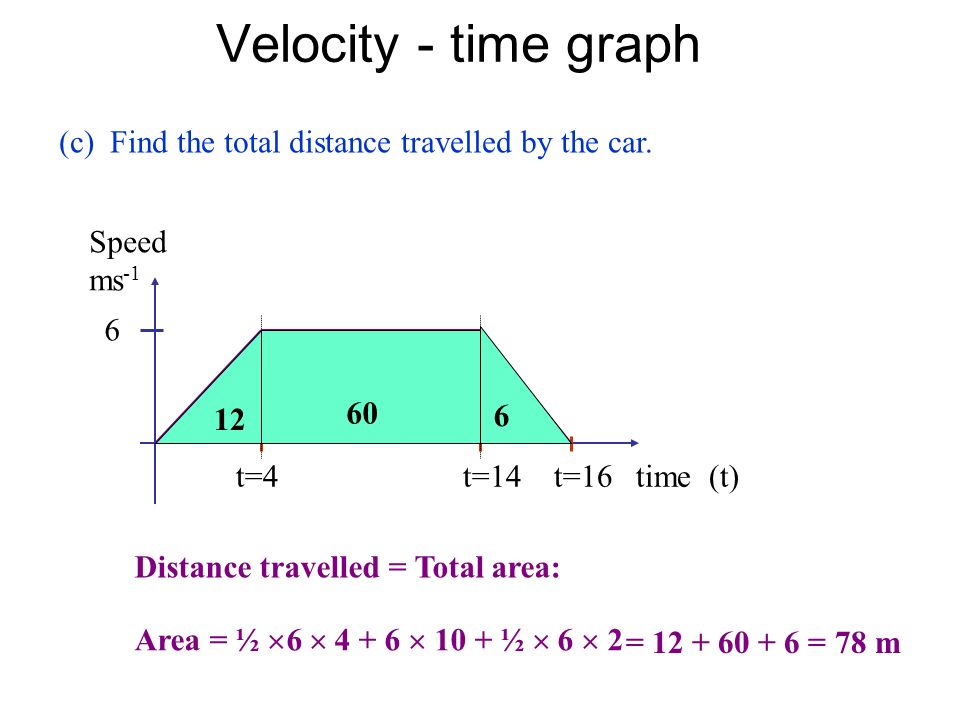
Area between point or curve in velocity-time graph and time axis
Area between point or curve in velocity-time graph and time axis = velocity x time = distance travelled
40
New cards
Uniform acceleration
When an object’s velocity changes at a constant rate.
41
New cards
When can the velocity squared equation be used?
Can be used to calculate uniform (constant) acceleration of an object when time taken is unknown.
42
New cards
Equation of motion (involves velocity squared)
(final speed)^2 = (initial speed)^2 + (2 x acceleration x distance moved)
v^2 = u^2 + 2as
v^2 = u^2 + 2as
43
New cards
How can directions be depicted for vector quantities?
\+ for up/right.
\- for down/left.
OR + for specified direction and - for opposite direction.
OR free body diagrams with arrows to show forces acting on object and the object’s direction of motion.
\- for down/left.
OR + for specified direction and - for opposite direction.
OR free body diagrams with arrows to show forces acting on object and the object’s direction of motion.