5.1 Probability rules

1. what is the probability of an event that is impossible? Suppose that a probability is approximated to be zero based on empirical results. Does this mean that the event is impossible?

What is the probability of an event that is impossible? (type an integer or a decimal)

2. suppose that a probability is approximated to be zero based on empirical results does this mean that the event is impossible?

yes or no?

0

No

what does it mean for an event to be unusual? Why should the cut off for identifying unusual events not always be 0.05?

an event is unusual if it has a low probability of occurring. The choice of a cutoff should consider the context of the problem.

fill in the blink

In probability, A(n) ___ Is any process that can be repeated in which the results are uncertain?

experiment

fill in the blink below

a ___ Is any collection of outcomes from a probability experiment?

event

is the following a probability model? What do we call the outcome “yellow”?

1. is the table above an example of a probability model?

2. what do we call the outcome “yellow”?

1. no, because the probabilities do not sum to one

2. impossible event

why is the following not a probability model?

This is not a problem model because at least one probability is less than zero

which of the following numbers could be the probability of an event?

1, -0.53, 0, 0.28, 0.04, 1.15

1, 0, 0.28, 0.04

in a certain card game, the probability that a player is dealt a particular hand is 0.33. Explain what this probability means. If you play this card game 100 times, will you be dealt this hand exactly 33 times? Why or why not?

B. The probability 0.33 means that approximately 33 out of every 100 dealt hands will be that particular hand. No, you will not be dealt this hand exactly 33 times since the probability refers to what is expected in the long-term, not short term.

suppose you Toss a coin 100 times and get 82 heads and 18 tails based on these results what is the estimated probability that the next flip results in a tails?

approximately 0.18

if a person rolls a six sided dye and then flips a coin, describe the sample space of possible outcomes using one, two, three, four, five, six for the dye outcomes and H, T for the coin outcomes type the outcomes in the form 1H, which would be the outcome of rolling a one and flipping heads.

1. The sample space (S) is what?

1. 1H, 2H, 3H, 4H, 5H, 6H, 1T, 2T, 3T, 4T, 5T, 6T

let the sample space be

1,2,3,4,5,6,7,8,9,10

Suppose the outcomes are equally likely compute the probability of the event

E= 1,3,5,6

0.4

let the sample space be

1 through 10

Suppose the outcomes are equally likely compute the probability of the event

E= “ An odd number less than 10”

0.5

A survey of 100 randomly selected high school students determined that 43 play organized sports.

A. What is the probability that a randomly selected high school student?

B. if 1000 high school students were sampled, it would be expected __ __ Of them play organize sports.

A. 0.43

B. about 430

A bag of 100 tulip bulbs purchased from a nursery contains 30 red, tulip bulbs, yellow, tulip bulbs, and 30 purple tulip bulbs.

A. What is the probability that a randomly selected to a bulb is red?

B. What is the probability that a randomly selected tulip bulb is purple?

C. if 100 tulips were sampled with replacement, Won would expect __ of the bulbs to be red and __ __ of the bulbs to be purple.

A. 0.3

B. 0.3

C. about 30 red tulips, 30 purple tulips

in a certain game of chance, a wheel consist of 36 slots numbered 00, 0, 1, 2,….34.

To play the game, a metal ball is spun around the wheel, and it is allowed to fall into one of the numbered slots

A. Determine the sample space choose the correct answer below

B. determine the probability that the metal ball falls into the slot marked six. (round 4 decimal places)

C. if the wheel is fun, 1000 times it is expected that __ __ of those times results in the ball landing in slot 6. (type a whole number)

D. The probability that the metal ball lands in an odd slot is? (round four decimal places)

A. 00,0,1,2…..34

B. 0.0278

C. 28

D. 0.4722

A police officer randomly selected 600 police records of larceny thefts the accompanying data represent the number of offenses for various type types of larceny thefts

A. Construct a probability model for type of larceny theft (round to three decimal places as needed)

B. Are coin operated machine, larcenies Unusual?

C. Are larceny from buildings unusual?

A. picture above

B. yes, because coin operated machine is less than 0.05

C. No, because larcenies from buildings is greater than 0.05

A baseball player hit 60 home runs in a season of the 60 home runs, 15 went to right field, 19 went to right centerfield, 12 went to centerfield, 12 went to left centerfield and 2 went to left field

A. What is the probability that randomly selected home run was hit to right field (round three decimal)

B. What is the probability that a randomly selected home run was hit to left field (round 3 decimal)

C. Was it unusual for this player to hit a home run To Leftfield? Explain.

A. 0.25

B. 0.033

C. yes, because left field is less than 0.05

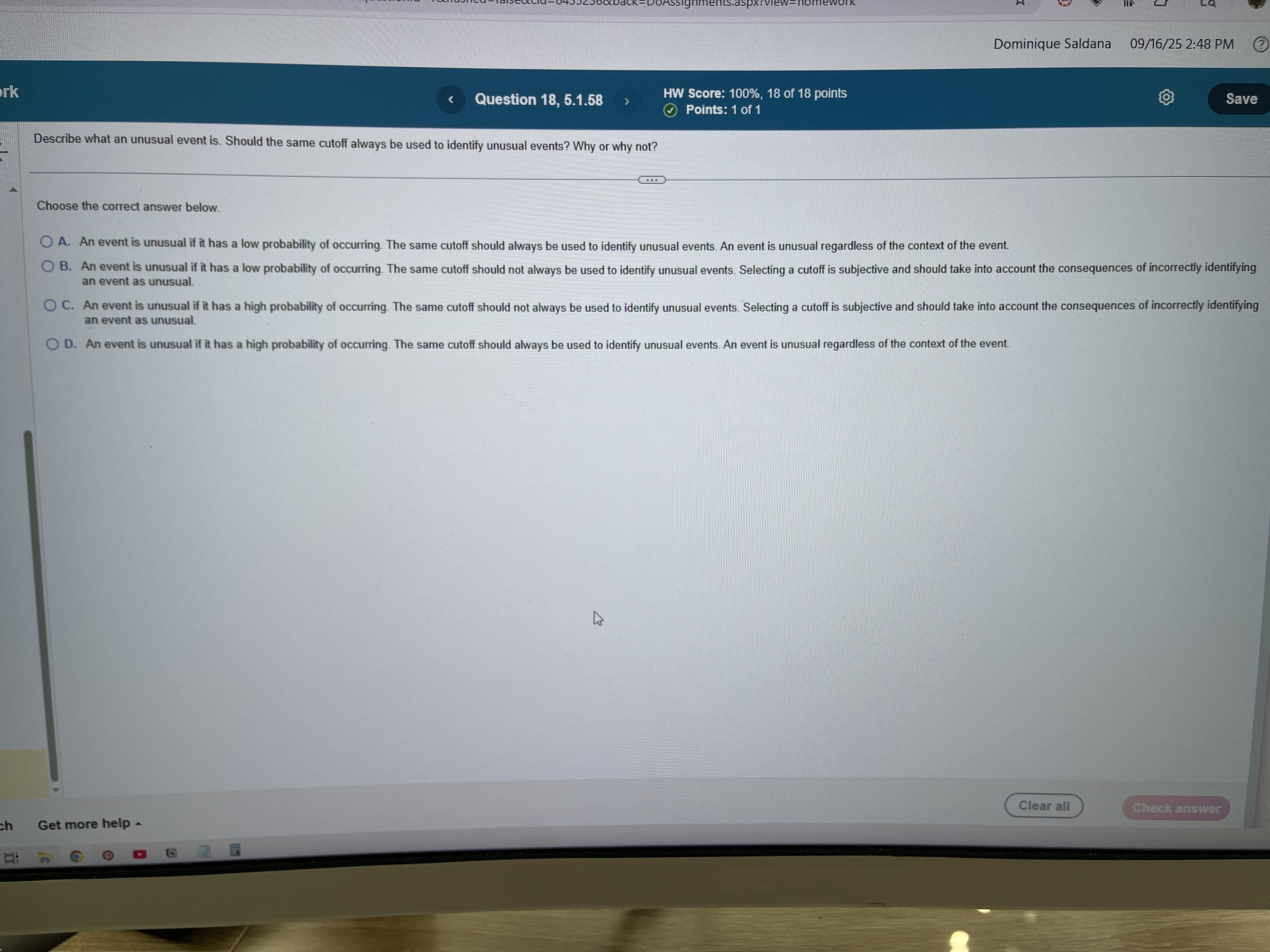
describe What an unusual event is, should the same cut off always be used to what identify unusual events why or why not?

B. An event is unusual because it has a low probability of occurring the same cutoff should not always be used to identify unusual events, selecting a cutoff is subjective, and should take into account the consequences of incorrectly, identifying an event as unusual