Fyzika new

Jaká tři skupenství hmoty rozlišujeme? (1b.) 1

pevné plynné kapalné

Co jsou to extenzivní a intenzivní veličiny? Uveďte příklady. (1b.) 2

Jak zní I. postulát termodynamiky? (1b.) 3

Jak zní II. postulát termodynamiky? (1b.) 4

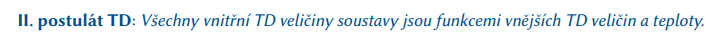
Jak je definován kvazistatický neboli rovnovážný děj? (1b.) 5

Jak je definován vratný termodynamický děj? (1b.) 6

Jak zní Nultý zákon termodynamiky? (1b.) 7

Napište převodní vztah mezi Celsiovou a termodynamickou (Kelvinovou) stupnicí. (1b.) 8

Jaké rozlišujeme způsoby přenosu energie do či ze soustavy? Popište je. (1b.) 9

Způsoby přenosu energie 1⃣ Teplo QQQ

• přenos energie vlivem rozdílu teplot

2⃣ Práce WWW

• přenos energie působením makroskopických sil
  (objemová, elektrická, povrchová…)

3⃣ Tok hmoty

• energie je přenášena spolu s částicemi, které do soustavy vstupují nebo ji opouštějí

• přenáší se:

  • vnitřní energie

  • kinetická energie

  • potenciální energie

  • případně chemická energie

Jak je definována objemová práce. Uveďte příklad. (1b.) 10

Jakými předpoklady je definován ideální plyn. (1b.) 11

okonale pružná: Energie se zachovává. Tělesa odskakují

Napište vztah mezi tlakem a teplotou pro izochorický děj. (1b.) 12

Napište První zákon termodynamiky v diferenciálním tvaru a popište veličiny, které se ve vztahu vyskytují. (1b.) 13

Napište vztah definující tepelnou kapacitu. (1b.) 14

Napište vztah definující entalpii. (1b.) 15

Napište Mayerův vztah. (1b.) 16

Napište vztah pro tepelnou účinnost ideálního Carnotova cyklu. (1b.) 17

Napište vztah pro statistickou (Boltzmannovu) entropii. (1b.) 18

• WWW … počet mikrostavů odpovídajících danému makrostavu

• SSS … entropie

• kBk_BkB​ … Boltzmannova konstanta

Napište Clausiova nerovnost v diferenciálním tvaru (matematická formulace 2. TD zákona). (1b.) 19

Napište Clausiova nerovnost v integrálním tvaru (matematická formulace 2. TD zákona). (1b.) 20

Jak zní Třetí termodynamický zákon. (1b.) 21

Jaké skupenské přeměny rozlišujeme? (1b.) 22

Napište vztah pro délkovou teplotní roztažnost. (1b.) 23

Napište vztah pro objemovou teplotní roztažnost. (1b.) 24

Napište znění Ekvipartičního teorému. (1b.) 25

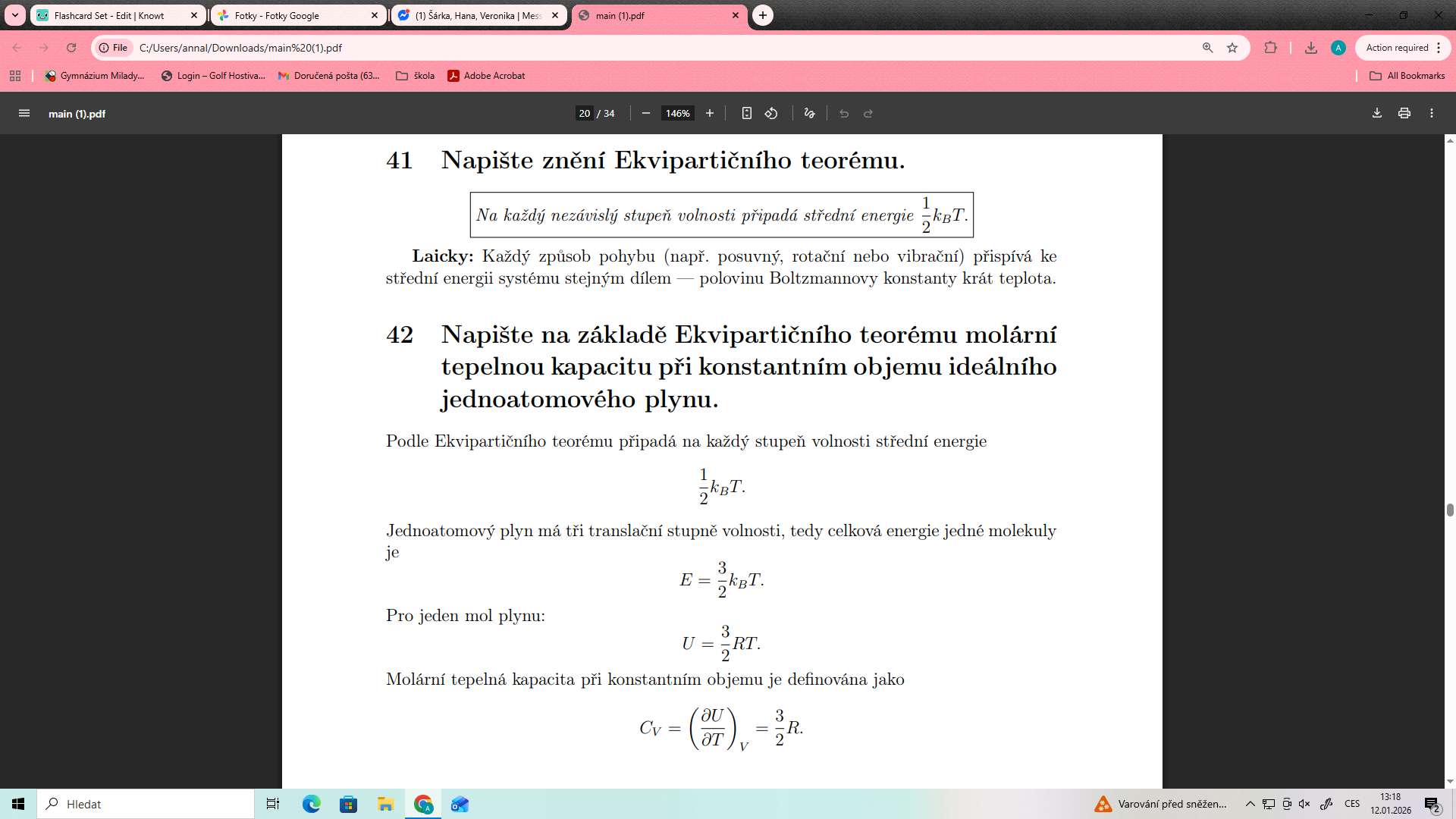
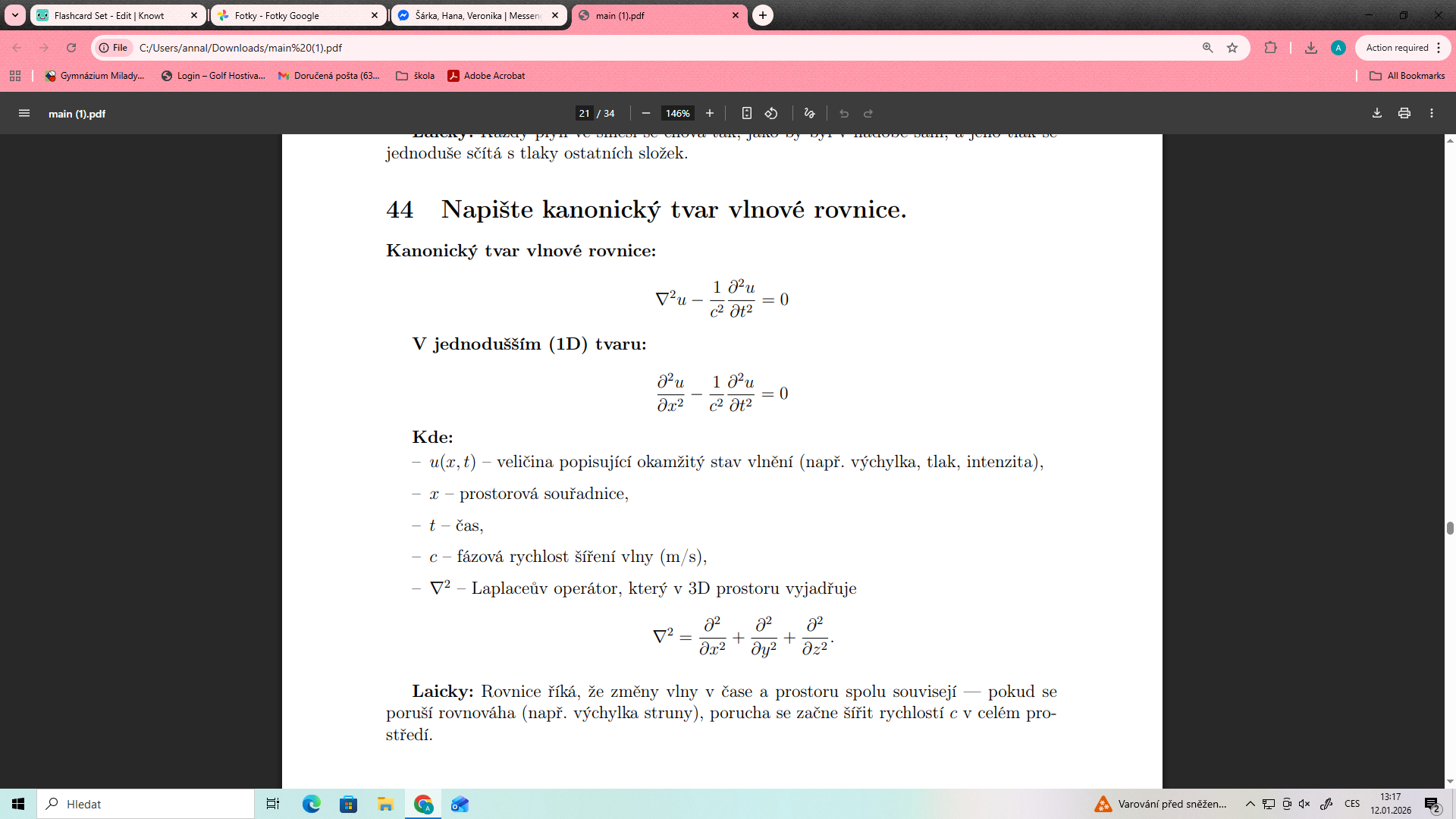
Napište kanonický tvar jednorozměrné vlnové rovnice. (1b.) 26

Napište vztah pro fázovou rychlost pro harmonickou vlnu. (lb.) 27

Napište vlnovou rovnici pro rovinnou vlnu postupující pouze jedním směrem. (1b.) 28

Co chápeme pod pojmem disperze? Jak vypadá obecný zápis disperzní relace? (1b.) 29

Zápis ω=ω(k)\omega = \omega(k)ω=ω(k) říká, že frekvence není nezávislá, ale je funkcí vlnového čísla.

Jaký je rozdíl mezi akustickou rychlostí a rychlostí šíření akustické vlny. (1b.) 30

Jak definujeme akustický tlak. (1b.) 31

Šíří se v tekutinách vlna podélná či příčná? Zdůvodněte. (1b.) 32

Napište vztah pro výpočet hladiny akustického tlaku. (1b.) 33

Jaký je geometrický vztah mezi mezi vektory elektrické intenzity, magnetické intenzity a vlnového vektoru. (1b.) 34

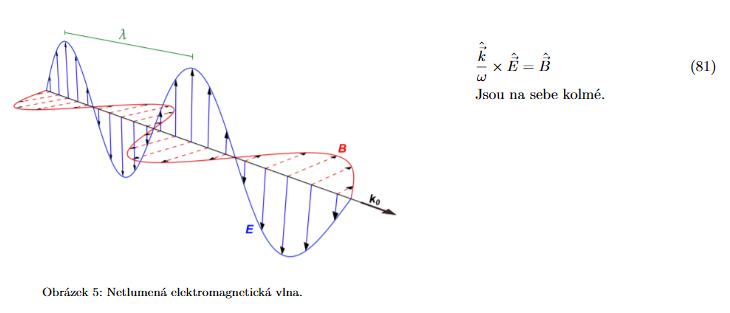
Je elektromagnetická vlna v izotropním prostředí vlnou podélnou či příčnou? Zdůvodněte. (1b.) 35

Napište vztah pro Poyntingův vektor. (1b.) 36

Poyntingův vektor S\mathbf{S}S popisuje směr a velikost toku elektromagnetické energie.

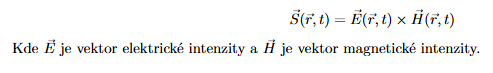
Napište vztah pro Brewsterův úhel. (1b.) 37

Odražené světlo je při tomto úhlu zcela lineárně polarizované (kolmo k rovině dopadu). Polarizace určuje, jak elektrické pole kmitá v prostoru.

Napište vztah pro mezní úhel. (1b.) 38

mezní úhel je úhel dopadu, při kterém nastává úplný odraz světla.

Napište vztah pro optickou dráhu. (1b.) 39

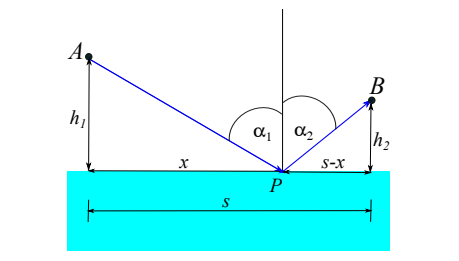
Napište zákon odrazu spolu s vysvětlujícím obrázkem. (1b.) 40

α1 = α2 . (18.8) 167 Tento vztah je vyjádřením hledaného Zákona dopadu a odrazu, který nám říká:Úhel dopadu paprsku je roven jeho úhlu odrazu

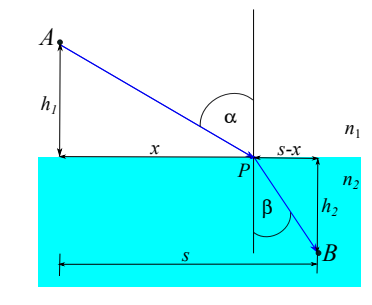
Napište zákon lomu (Snellův zákon) spolu s vysvětlujícím obrázkem. (1b.) 41

sin α = n sin β , (18.15) kde n = n2/n1 je relativní index lomu

Napište vztah pro vektor magnetické indukce rovinné elektromagnetické vlny šířící se v obecném směru. (1b.) 42

Napište podmínku konstruktivní interference dvou monochromatických světelných paprsků. (1b.) 43

Napište podmínku destruktivní interference dvou monochromatických světelných paprsků. (1b.) 44

Napište znění Fermatova principu. (1b.) 45

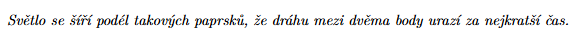
Napište vztah pro index lomu, znáte-li rychlost šíření světla v daném prostředí. (1b.) 46

Napište vztah pro rychlost šíření rovinné elektromagnetické vlny v dielektriku s permitivitou a permeabilitou μ. (16.) 47

Napište definiční vztah pro emisivitu tělesa. (1b.) 48

Jak nazýváme stejné částice, jejichž soubor má symetrickou vlnovou funkci? (1b.) 49

Jak nazýváme stejné částice, jejichž soubor má antisymetrickou vlnovou funkci? (1b.) 50

Napište znění Pauliho vylučovacího principu. (1b.) 51

Napište vztah pro hybnost fotonu. (1b.) 52

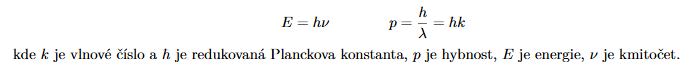
Napište vztah pro energii fotonu. (1b.) 53

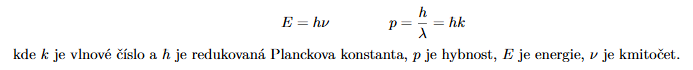
Uveďte základní 4 interakce, ze kterých se sestává vesmír. (lb.) 54

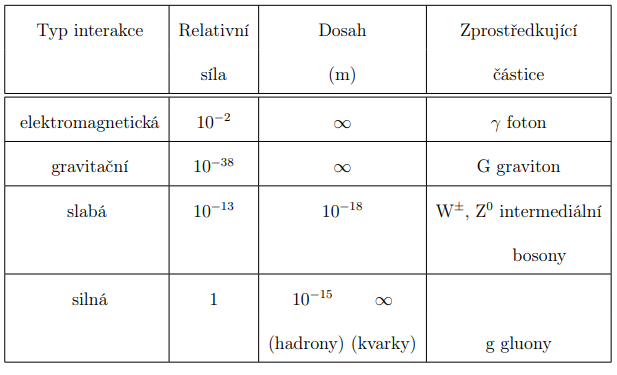
Napište Fouierův zákon v jednorozměrném tvaru. (2b.) 55

Napište stavovou rovnici ideálního plynu. (2b.) 56

Napište van der Waalsovu stavovou rovnici. (2b.) 57

Napište kalorimetrickou (směšovací) rovnici. (2b.) 58

J/(kg·K))

Napište První zákon termodynamiky v diferenciálním tvaru. (2b.) 59

práce která vykonává soustava na okolí

Napište diferenciální tvar 1. TD zákona pro ideální plyny konající objemovou práci. (2b.) 60

Napište Thomsonovu (Kelvinovu) formulaci Druhého zákona termodynamiky. (2b.) 61

Thomsonova (Kelvinova) formulace: Je nemožné cyklickým dějem odnímat jednomu tělesu teplo a to bezezbytku měnit v kladnou práci.

Napište vztah pro účinnost obecného tepelného motoru spolu s vysvětlujícím obrázkem. (2b.) 62

Nakreslete p-V digram pro ideální Carnotův cyklus a popište jednotlivé děje, ze kterých se sestává. (2b.) 63

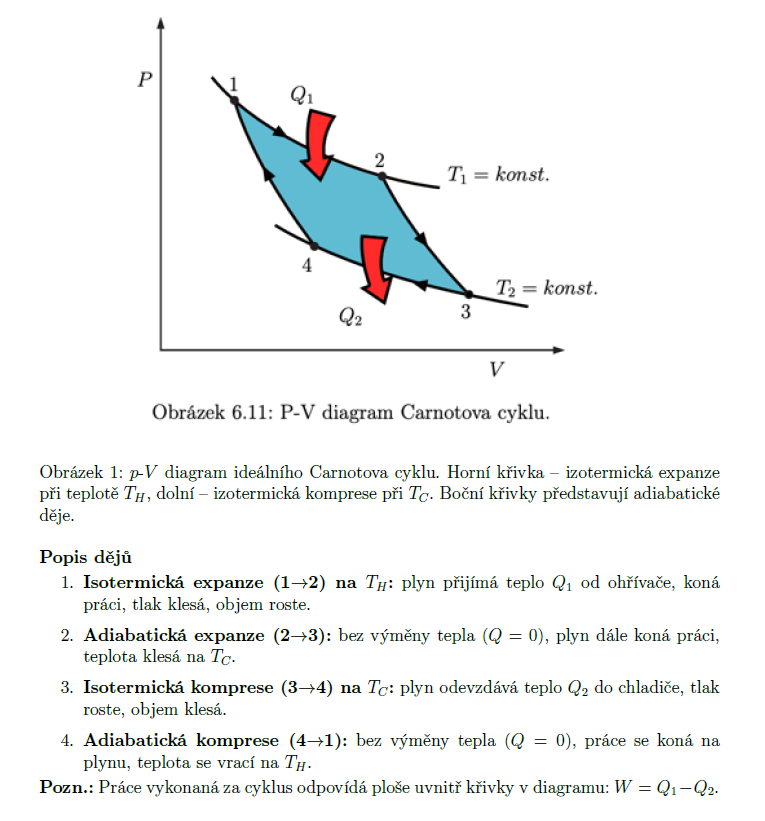
Napište znění první a druhé Carnotovy věty. (2b.) 64

Napište rovnici vyjadřující sloučení 1. a 2. TD zákona do jednoho vztahu pro ideální plyn konající objemovou práci. (2b.) 65

Napište Clausiovu-Clapeyronovu rovnici. (2b.) 66

J/kg

Nakreslete fázový $p-T$ diagram pro pro jednosložkovou soustavu. Popište jednotlivé části diagramu spolu s významnými body. (2b.) 67

Napište vztah vyjadřující pomocí termodynamické teploty střední kinetickou energii molekul ideálního plynu. (2b.) 68

Napište vztah vyjadřující Maxwellovo-Boltzmannovo rozdělení rychlostí ideálního plynu. (2b.) 69

Napište vztah pro Boltzmannovo rozdělení energií. (2b.) 70

Boltzmannova konstanta (kBk_BkB​) je fyzikální konstanta, která spojuje teplotu tělesa s jeho vnitřní energií na úrovni jednotlivých částic

Napište vlnovou rovnici pro tenkou strunu spolu se vztahem pro rychlost šíření vlny na této struně. Napište o jaký druh vlnění se jedná. (2b.) 71

Lineární hustota μ=m/l hmotnost na jednotku délky

Napište obecné d'Alembertovo řešení jednorozměrné vlnové rovnice a ukažte, že je skutečně jejím řešením. (2b.) 72

Napište vlnovou rovnici pro rovinné vlny a její řešení pro případ, že se jedná o harmonickou vlnu šířící se ve směru daném vlnovým vektorem k. (2b.) 73

Napište vlnovou rovnici pro kulové vlny a její obecné d'Alembertovo řešení. (2b.) 74

Jak je definováno vlnové číslo pomocí kruhového kmitočtu? Jak je definované vlnové číslo pomocí vlnové délky? Co nám udává směr vlnového vektoru? (2b.) 75

Napište vztah pro kmitočet, který zaznamená pozorovatel, který se pohybuje rychlostí $v_{P}$ vůči zdroji, který se vzhledem k prostředí, jímž se vlna šíři, nepohybuje. (2b.) 76

Napište vztah pro kmitočet, který zaznamená pozorovatel, jenž se vzhledem k prostředí, jímž se vlna šíři, nepohybuje a pohybuje se vůči pozorovateli jen zdroj rovinných vln rychlostí $v_{Z}$. (2b.) 77

Dopplerův jev je změna vnímané frekvence (nebo vlnové délky) vlnění, když se zdroj a pozorovatel pohybují vůči sobě.

Napište vztah pro výpočet grupové rychlosti a fázové rychlosti. Jak je definována normální a anomální disperze. (2b.) 78

Odvoďte obecný vztah mezi grupovou a fázovou rychlostí. (2b.) 79

Napište soustavu linearizovaných rovnici popisující akustické vlny v ideální tekutině. (2b.) 80

Napište Poyntingovu bilanční rovnici v diferenciálním tvaru. (2b.) 81

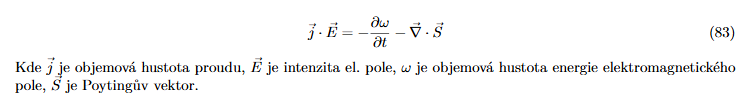
Napište vztah pro obecnou eliptickou polarizaci. (2b.) 82

• Ex​,Ey​ … okamžité složky elektrického pole

• E0x,E0yE_{0x}, E_{0y}E0x​,E0y​ … amplitudy složek pole v osách xxx, yyy

• δ\deltaδ … fázový rozdíl mezi oběma složkami

Napište podmínku lineární polarizace rovinné elektromagnetické vlny. (2b.) 83

Napište podmínku kruhové polarizace rovinné elektromagnetické vlny. (2b.) 84

Definujte TE a TM polarizaci rovinných elektromagnetických vln spolu s vysvětlujícím obrázkem (2b.) 85

• Vlnové číslo kkk říká, jak husté jsou vlny v prostoru.

• Vlnový vektor k\mathbf{k}k navíc říká i směr šíření vlny.

Napište vztah pro intenzitu světla rovinné elektromagnetické vlny ve vakuu, znáte-li vektor elektrické intenzity E. (2b.) 86

Napište interferenční rovnici dvou monochromatických elektromagnetických rovinných vln (obecně nekoherentních). (2b.) 87

Napište Helmholtzovu rovnici pro vektor eletkrické intenzity E. (2b.) 88

Napište, za jakých podmínek je možné použít paprskovou (geometrickou) optiku. (2b.) 89

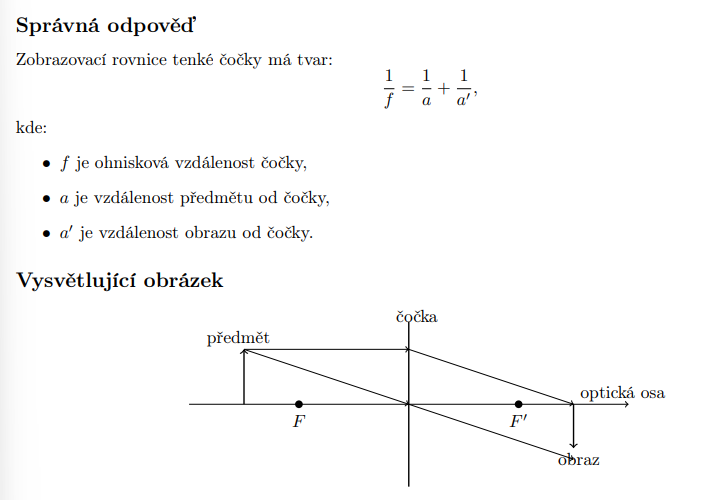
Napište zobrazovací rovnici pro tenkou čočku spolu s vysvětlujícím obrázkem. (2b.) 90

ohnosko je bod do kterehi se po pruchodu cockou sbihaji paprsky rovnomeze s opt osou

Napište zobrazovací rovnici pro lom na kulové ploše spolu s vysvětlujícím obrázkem. (2b.) 91

• $Z$ (Zdroj / Object): Bodový předmět nebo zdroj světla, ze kterého vychází paprsek.

• $V$ (Vrchol): Vrchol kulové plochy. Je to bod, kde optická osa protíná rozhraní (čočku/plochu). Všechny vzdálenosti se obvykle měří od tohoto bodu.

• $S$ (Střed křivosti): Geometrický střed koule, jejíž částí je ona lámavá plocha.

• $P$ (Obraz / Image): Bod, kde se paprsek po lomu protne s optickou osou. Zde vzniká obraz bodu $Z$.

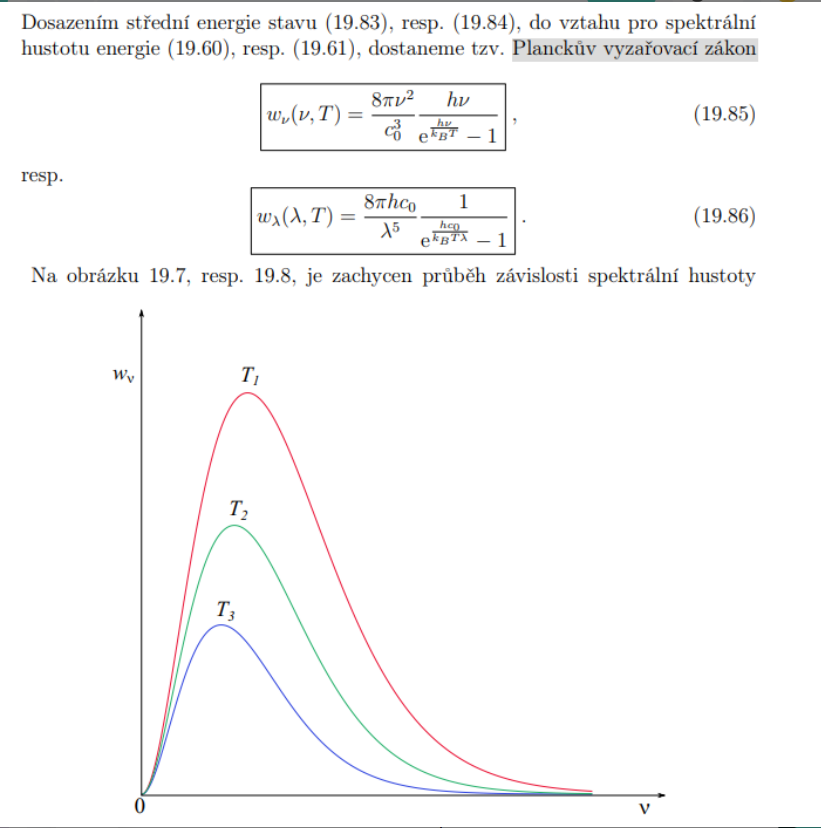
Napište Planckův vyzařovací zákon v závislosti na vlnové délce spolu s obrázkem zachycujícím příslušné průběhy pro teploty $T{1}

Proměnné:

• w_nu (nu, T): Spektrální hustota energie (frekvenční) – jednotka: J.m^-3.s

• w_lambda (lambda, T): Spektrální hustota energie (vlnová) – jednotka: J.m^-4

• nu (ný): Frekvence záření – jednotka: Hz nebo s^-1

• lambda: Vlnová délka – jednotka: m

• T: Termodynamická teplota – jednotka: K (Kelvin)

Konstanty:

• h: Planckova konstanta – jednotka: J.s

• c0: Rychlost světla ve vakuu – jednotka: m.s^-1

• kB: Boltzmannova konstanta – jednotka: J.K^-1

Napište Planckův vyzařovací zákon v závislosti na kmitočtu spolu s obrázkem zachycujícím příslušné průběhy pro teploty $T{1}

Proměnné:

• w_nu (nu, T): Spektrální hustota energie (frekvenční) – jednotka: J.m^-3.s

• w_lambda (lambda, T): Spektrální hustota energie (vlnová) – jednotka: J.m^-4

• nu (ný): Frekvence záření – jednotka: Hz nebo s^-1

• lambda: Vlnová délka – jednotka: m

• T: Termodynamická teplota – jednotka: K (Kelvin)

Konstanty:

• h: Planckova konstanta – jednotka: J.s

• c0: Rychlost světla ve vakuu – jednotka: m.s^-1

• kB: Boltzmannova konstanta – jednotka: J.K^-1

Napište Wienův posunovací zákon. (2b.) 94

Napište Stefanův-Boltzmannův zákon. (2b.) 95

Napište stacionární tvar Schrödingerovy rovnice. (2b.) 96

Jednorozměrnou vlnovou funkci reprezentující materiálové vlny ta vidlicka

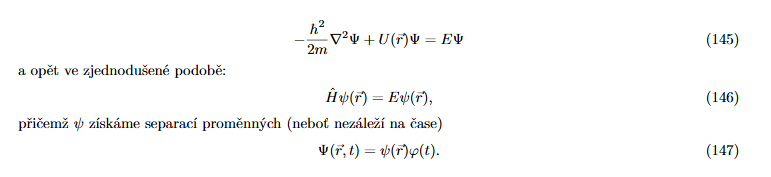
Napište nestacionární tvar Schrödingerovy rovnice. (2b.) 97

Popisuje časový vývoj kvantového stavu částice.

Napište Bornovu interpretaci vlnové funkce a příslušnou normovací podmínku. (2b.) 98

Napište vztah pro relativistickou energii volné částice o hybnosti p a klidové hmotnosti $m_{0}$. (2b.) 99

Napište vztah pro maximální kinetickou energii emitovaných elektronů z kovu o výstupní práci ozařovaném monochromatickou elektromagnetickou vlnou o frekvenci v. (2b.) 100