AB Topics

Inverse Trig Derivatives

• arcsin = 1/√1-u² * u’

• arccos = -1/√1-u² * u’

• arctan = 1/1+u² * u’

• arccot = -1/√1+u² * u’

• arcsec = 1/u√u²-1 * u’

• arccsc = -1/u√u²-1 * u’

• log_au = 1/(u ln a) * u’

• a^u=a^ulna*u’

d/dx[f^-1(x)]=1/f’(f^-1(x))

e and ln rules

f’(x) ∫f(x)

e^u e^u *du e^u/du

lnu 1/u * du

1/u power rule lnu/du

Integral to Summation

_a∫^bk^p = ∑ᵇ⁻ᵃ⁄ₙ(a+⁽ᵇ⁻ᵃ⁾ᵏ⁄ₙ)^p

Trig Identities

sin²x+cos²x=1

tan²+1=sec²x

cot²x+1=csc²x

VOLUME FORMULAS

Disk: π∫(r²)

Washer: π∫(big r)²-(small r)²

Shells: 2π∫r*h

Shells with gap: 2π∫r(big height-small height)

Cross Sections:

Semi-circle: ∫½πr² r= ᶠ⁽ˣ⁾⁻ᵍ⁽ˣ⁾⁄₂

Equilateral Triangle: ∫(√3)/4 s² s=f(x)-g(x)

Isosceles Right Triangle: ∫½s² s=f(x)-g(x)

Logistic Growth:

dP/dt=kP(1-P/L) or dP/dt=kP((L-P)/L)

k=constant, P=population at time t, L=carry capacity

BC Topics

Euler’s Method: y_new=y_old-y’∆x

Integration by Parts: ∫udv=uv-∫vdu

Arc Length: ∫√1+(f’(x))²

Parametric Formulas

Slope: (dy/dt)/(dx/dt) = dy/dx

Equation: y-y₁=m(x-x₁)

2nd Derivative: d²y/dx²= (d/dx (dy/dx)) / (dx/dt)

Arc Length: ∫√(dy/dt)²+(dx/dt)²

Speed: √(dy/dt)²+(dx/dt)²

Position: x(t)+∫x’(t) , y(t)+∫y’(t)

Polar Formulas

x=rcosθ

y=rsinθ

r=asin(nθ)

r=acos(nθ)

a=radius; n=odd → #of petals; n=even → 2n=petals; cos begins on x axis; sin begins @ 90/petals

r=2asinθ → circle centered on y axis

r=2acosθ → circle centered on x axis

Limacons: r=a±b(sin or cos)θ

a/b < 1 → inner loop

a/b = 1 → cardioid

1<a/b<2 → dent

a/b > 2 → bulge

Lemniscate: r²=a²(sin or cos) 2θ

Spiral: r=aθ

Basic Area: ½∫r² dθ

Arc Length: ∫√r²+(dr/dθ)²

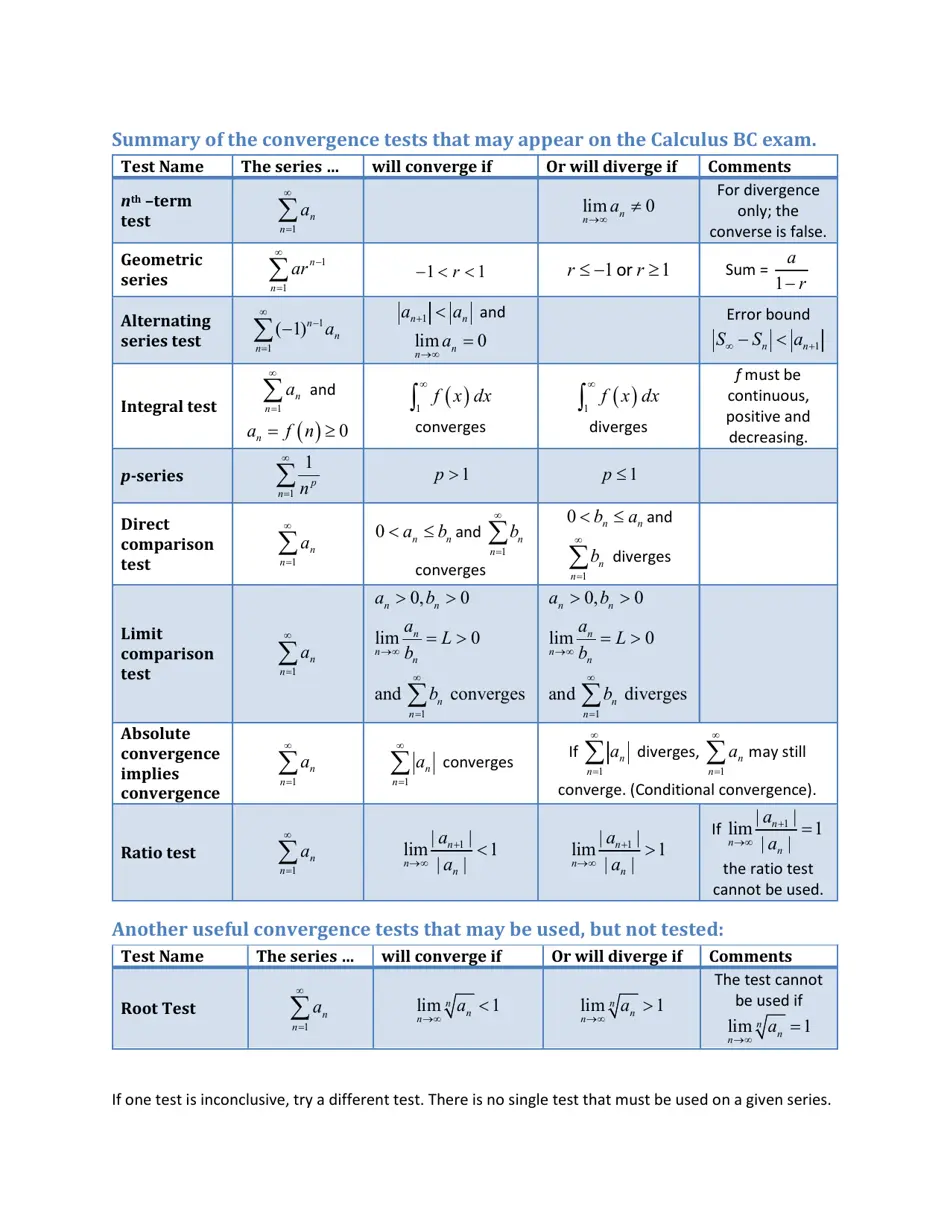
Series

La Grange Error Bound:

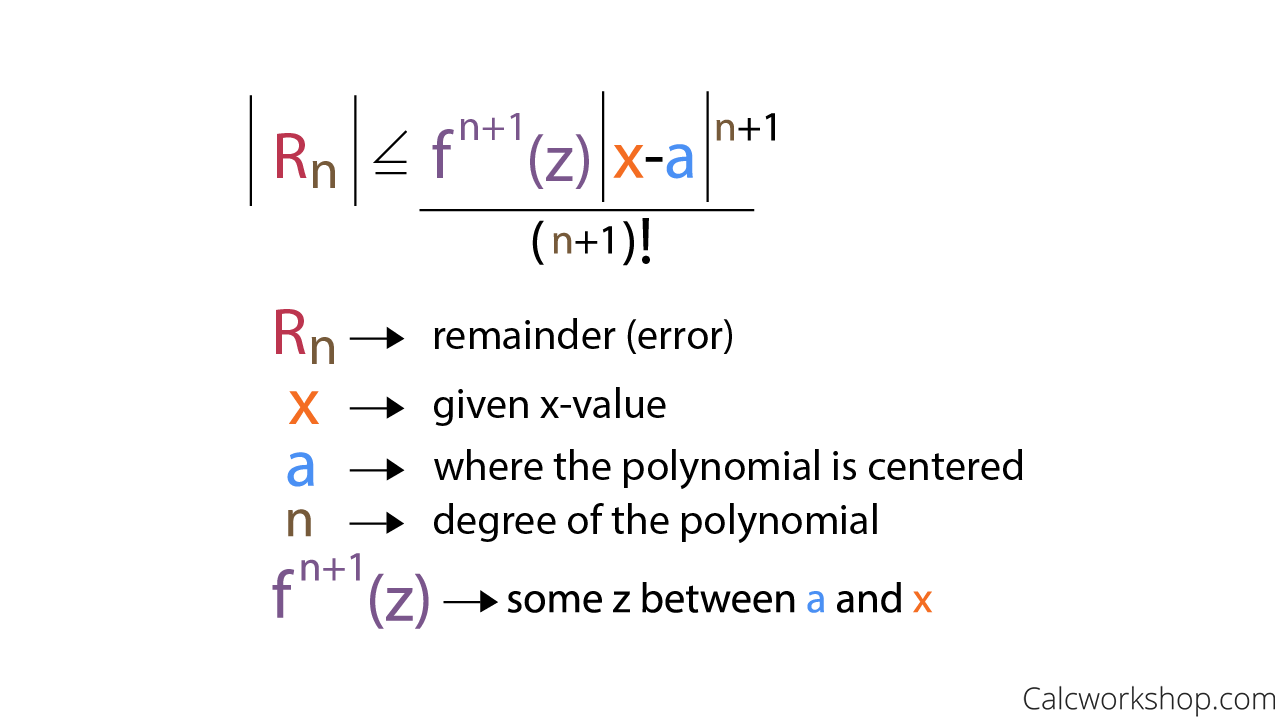
Alternating Series Error Bound:

Maclaurin Series:

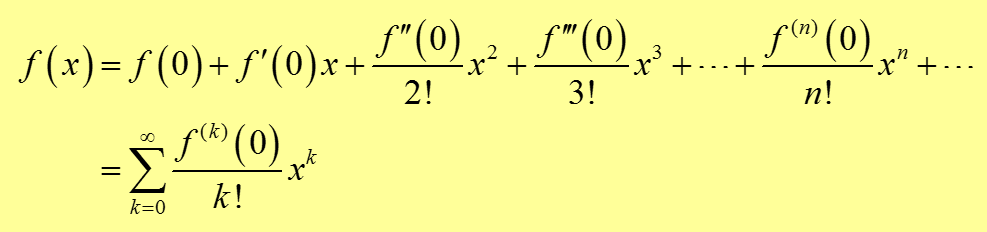
Taylor Series:

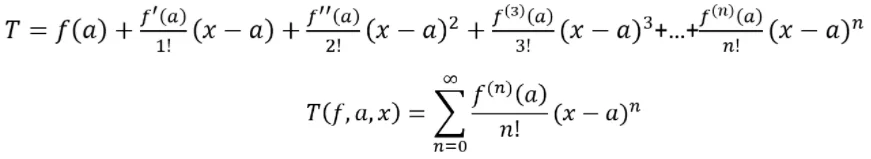
Power Series: (*memorize)