2 - cones & hyperplanes & convex functions & intro optimization

Convex cones video

Cone

Pointed Cone

Convex Cone

Finitely Generated Convex Pointed Cones

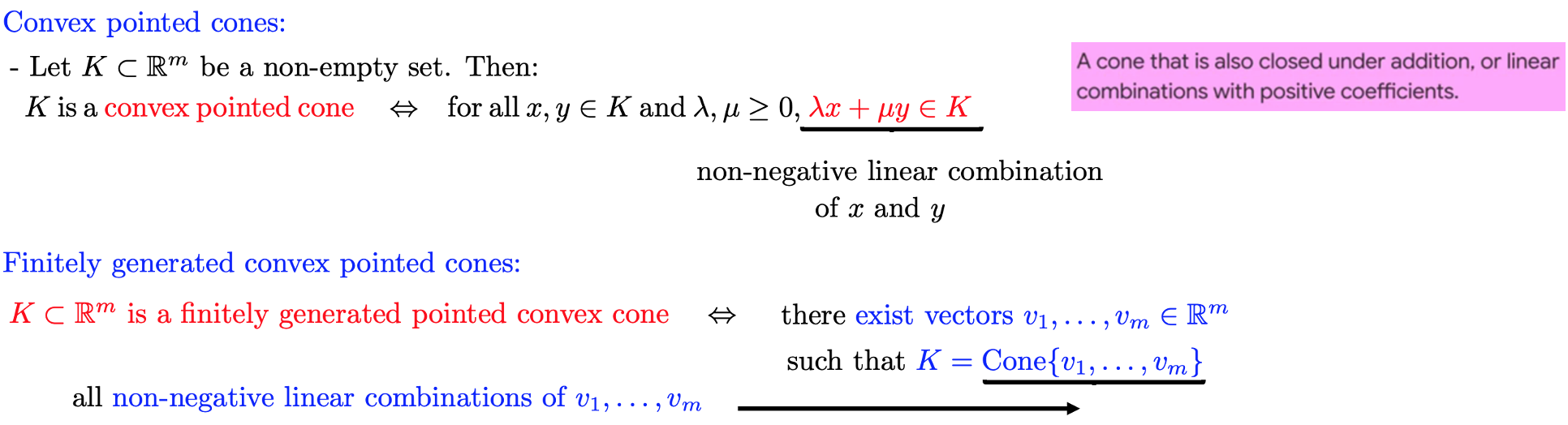
Polar Cone

Informal Definition

Polar Cone

Formal Definition + Visualization

Bipolar Theorem

Separation Theorem

How to determine supporting hyperplanes?

Polyhedral Convex Set

Polyhedral Convex Set

Properties

How to determine separating hyperplanes of polyhedral convex sets?

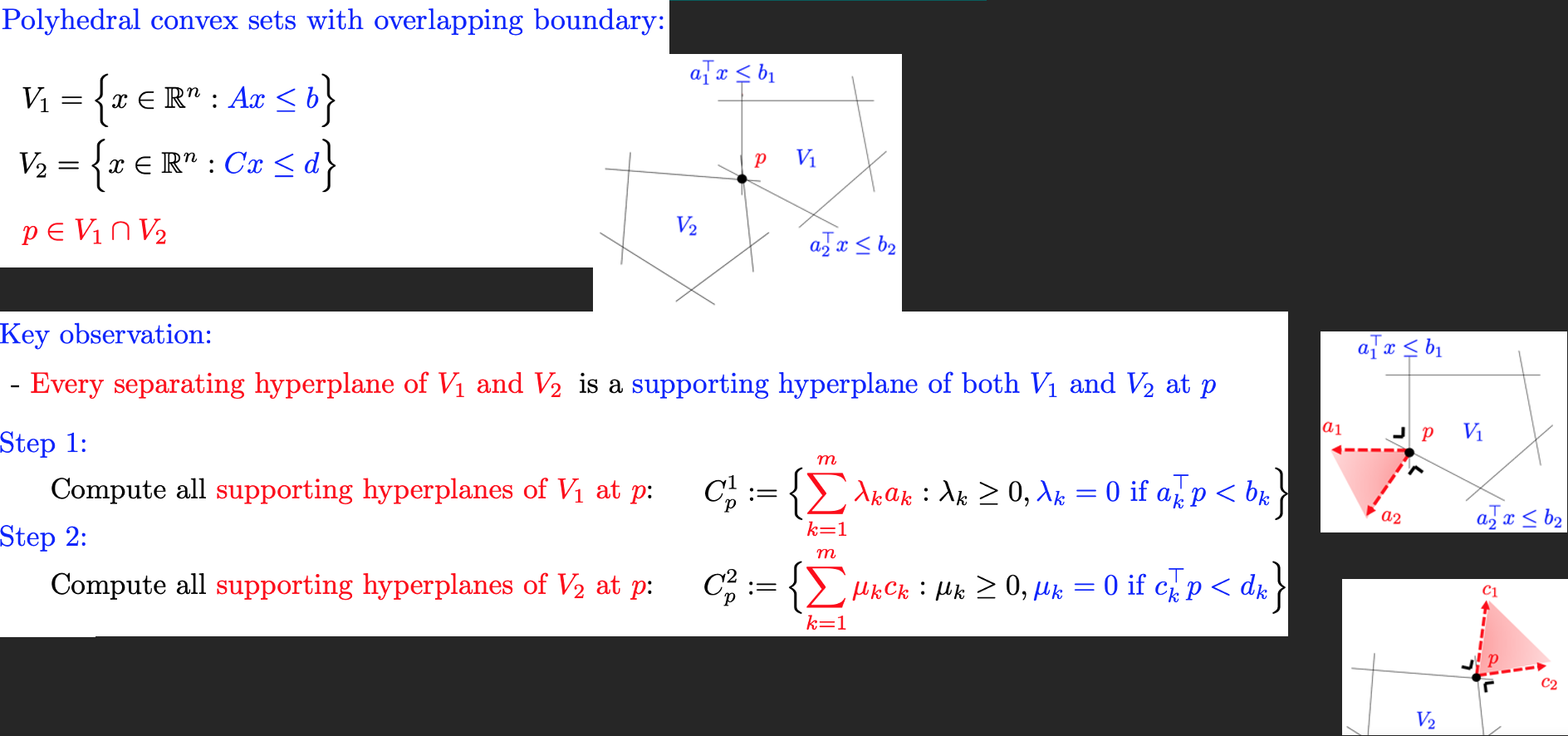
How to determine supporting hyperplanes?

Theorem

Slater condition

Extreme points

Intuition

Extreme points

Formal Definition

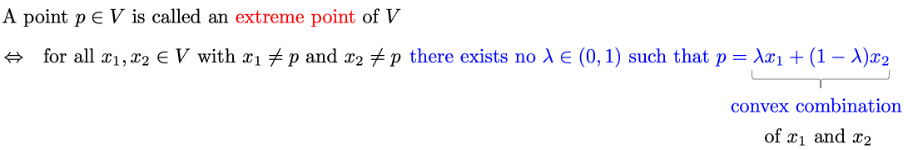
Extreme points

Informal Definition

Profile of V =

Collection of all extreme points of V

Theorem

Non-empty compact convex sets

Theorem

Summary of the geometric characterization of extreme points of a polyhedral set defined by linear inequalities

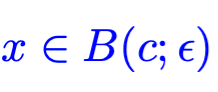
Convex functions and extreme values

Maxima and Minima

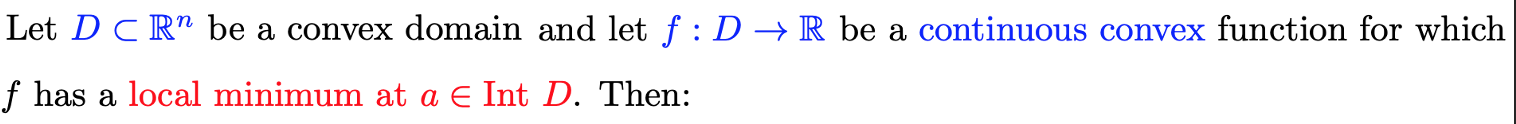
If D is compact …

Convexity in Optimization

Optimization

Convex Optimization

Linear Optimization

Linear Optimization Problems are most commonly expressed as Linear Programs:

From the course's convexity part, we recognize that:

The notation introduced so far may appear to be fairly restrictive, but in fact, it covers quite a range of problems, e. g.:

LP in Standard Form

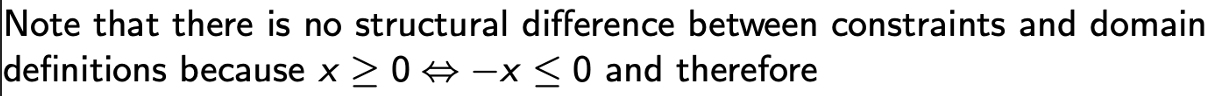
Any LP can be brought into standard form by following the transformation scheme:

Example of Linear Optimization Problems – Production Planning

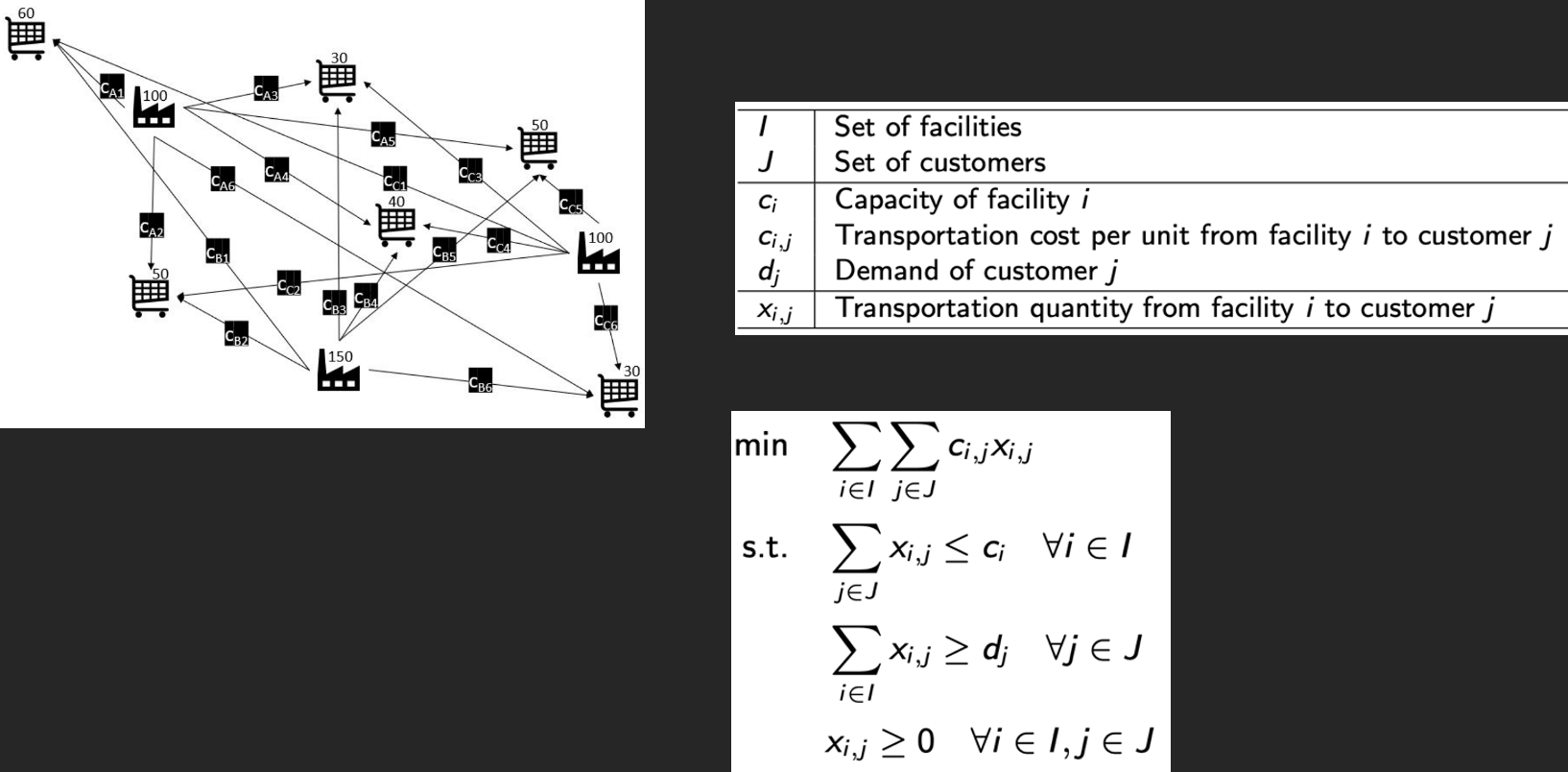
Example of Linear Optimization Problems – Transportation Problem

Fundamental Theorem of Linear Programming

When do we have at least one corner point?

How about (optimal) solutions?

Fundamental Theorem of Linear Programming

Implication

Theorem

Non-Optimal and Optimal Ccorner Points

Theorem

Non-Optimal and Optimal Ccorner Points

Proof

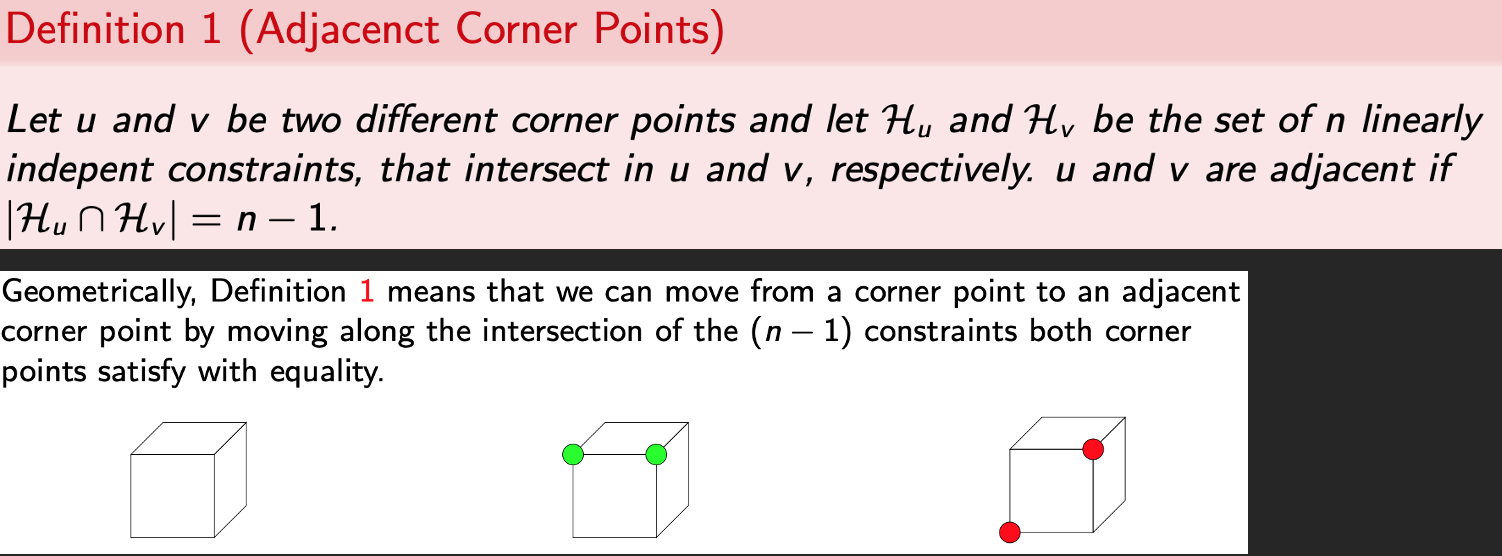
Definition

Adjacent Corner Points

+ geometric meaning