Physics Unit C Standing Waves And Doppler Effect

What is the droppler effect?

• The droppler effect is seen when the source( object, thing, person, etc that is causing the disturbance (waves) moves)

• The droppler effect is the apparent change in the frequency of a wave caused by the relative motion between the source of the wave and the observer.

• So, all in all, the doppler effect is a change in frequency interpreted by the observer due to the relative motion between the source and observer.

When the source is moving towards the observer, the sound(or whatever wave) is delivered at a ____________ frequency.

higher ( higher pitch- for sound waves)

When the source is moving away form the observer, the sound(or whatever wave) is delivered at a ____________ frequency

lower( for sound - lower pitch)

Who was the droppler effect described by?

The droppler effect was first describe in 1842 by Austian physicist Christian Doppler.

Why does the frequency increase when the source is approaching the observer? (In relation to the Doppler effect)

• In understanding this we can look at the velocity equation for waves V = fλ

• Based on this equation, when can see that frequency and wavelength are inversely proportional.

• When the source is moving towards the observer, the waves are compressed(compression).

• Thus, the wavelength is smaller, so the frequency is greater.

• The velocity of the sound waves remain the same because it depends on the medium not the distance.

Why does the frequency decrease when the source is moving away from the observer? ( In relation to the Doppler effect)

• In understanding this we can look at the velocity equation for waves V = fλ

• Based on this equation, when can see that frequency and wavelength are inversely proportional.

• When the source is moving towards the observer, the waves are further apart (rarefaction).

• Thus, the wavelength is larger, so the frequency is less.

• The velocity of the sound waves remain the same because it depends on the medium not the distance

When there is no relation motion between the source of the waves and the observer, like it they are both stationary, does the doppler effect still occur?

No

The Doppler Effect is all about relative motion. It only happens when either:

• The source is moving toward or away from the observer,

• The observer is moving toward or away from the source,

• Or both are moving with respect to each other.

Doppler effect formula ( stationary observer approaching source)

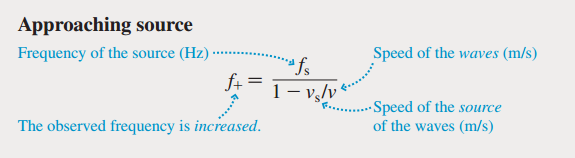
Doppler effect formula ( stationary observer receding source)

Doppler effect formula ( stationary source approaching observer )

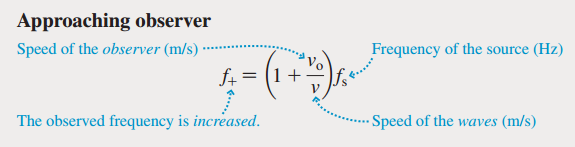
Doppler effect formula ( stationary source receding observer )

What does the principle of Superposition state?

If two or more traveling waves are moving through a medium and combine at a given point, the resultant position of the element of the medium at that point is the sum of positions due to the individual waves.

Linear waves

Waves that obey the superposition principle are called linear waves. (Generally, linear waves have amplitudes smaller than their wavelengths

What happens when two waves are traveling in the same direction with the same magnitude?

• Unlike objects, waves can occupy the same space at the same time.

• Therefore, waves no not collide when approaching each other instead they interfere via superposition.

Constructive Interference

Where two waves collide as a result of superposition and it result in an addition of the amplitude( greater wave pulse)

This usually happens when the waves are traveling in the same direction

Destructive Interference

• The waves travel in opposite directions, thus, the wave pulses cancel each other out when the two waves occupy the same space.

• When the wave has the same shape and amplitude but are on opposite sides. ( Total destructive interference- the two waves need to be perfect inversed of each other)

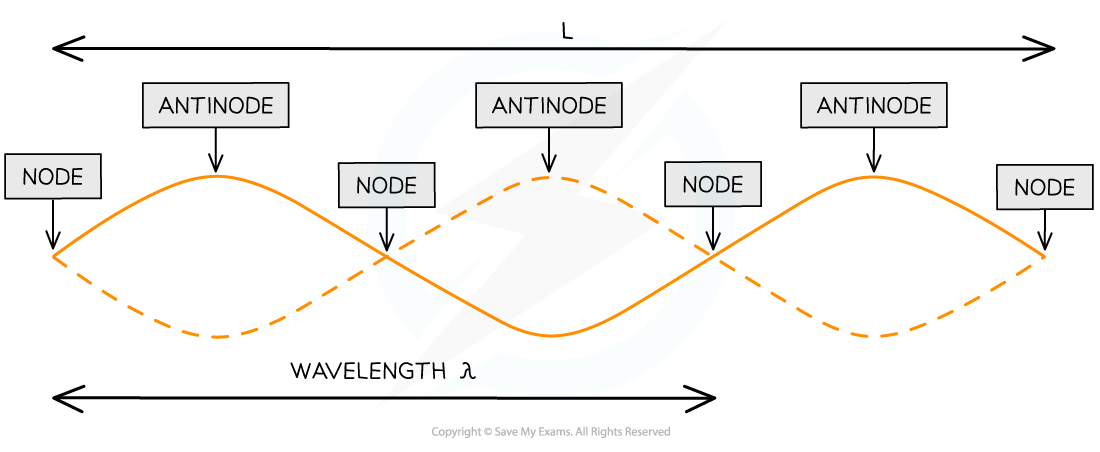
What are a standing waves?

Standing waves are waves that appear to be “Standing still” rather than traveling through a medium.

• They form when two waves have the same frequency and amplitude but travel in opposite directions and interfere with each other.

• Instead of moving left or right, the waves seem to just vibrate up and down in place.

• each end of standing waves are nodes.

Nodes

• Location of total destructive Interference

• These points are stationary

Antinodes

• Constructive Interference creates the largest amplitude

• Points are in motion

Why do standing waves occur?

Standing waves occur due to constructive and destructive interference between two waves moving in opposite directions.

• Standing Waves only occur at certain frequencies

• Standing waves usually happens when a waves reflects back on itself.

What causes standing waves to occur?

1. Reflection

2. Superposition

3. Resonance

Why do standing waves only occur at certain frequencies?

• Because the wave has to fit perfectly in the space (like a loop or half-loop on a string), only specific wavelengths—and therefore specific frequencies—will work.

• These "just right" frequencies are called resonant frequencies or natural frequencies. At other frequencies, the interference isn't stable, so no standing wave forms.

How does standing waves relate to resonance?

• 🌀 Standing waves form when a wave reflects and interferes with itself in just the right way—certain points stay still (nodes), and others vibrate a lot (antinodes).

• 🔊 Resonance happens when a system (like a string, air column, or tuning fork) is driven at one of its natural frequencies—a frequency at which it "likes" to vibrate. When this happens, the system responds with maximum amplitude.

• 🎯 So what's the connection?

  • Standing waves only form at resonant frequencies.

  • When a system is driven at a resonant frequency, the wave fits perfectly into the length of the system, creating constructive interference that builds up into a standing wave.

  • That’s why resonance causes standing waves, and standing waves are a visual and physical sign of resonance.

Are boundaries needed to cause standing waves?

Yes—boundaries are essential for standing waves to form. Without boundaries, you won't get the kind of reflection and interference needed to create a standing wave pattern.

📌 Why are boundaries needed?

Standing waves happen when:

1. A wave travels through a medium.

2. It hits a boundary (like the end of a string or a wall).

3. It reflects back.

4. The reflected wave interferes with the incoming wave.

5. If the conditions are right (like frequency and length), a standing wave forms.

⚠ No boundary = no reflection = no standing wave

If there's no boundary, the wave just keeps traveling and doesn't reflect back to interfere with itself. That means:

• No constructive/destructive interference pattern

• No nodes or antinodes

• Just a traveling wave, not a standing one

What counts as a boundary?

🧱 What counts as a boundary?

• Fixed end of a string (like a guitar string)

• Closed or open ends of a pipe (in wind instruments)

• Surfaces in a room (where sound waves reflect)

• Even things like walls in a tube or container

These boundaries cause reflection, which is crucial for creating the interference that produces standing waves.

What is beat?

A beat occurs when two waves of slightly different frequencies interfere. This results in a periodic loud- soft modulation of intensity( amplitude

C4.1 Standing wave

Produced by 2 waves travelling in opposite direction along same line with same f superposing.
Waves must have same λ and similar A.
They store energy (stationarily), rather than transferring like travelling/progressive waves
Each point on wave oscillates at diffferent speed, overall stationary.
Each point has different A depending on # of superposition herre

C4.2 Node- Antinode

Node: A=0, separated by ^λ/₂ : destructive interference: cancel
Antinode: A=max, also sep. by ^λ/₂: constructive inter.: added A’ds

Fixed positions, only move up down (vertical), dont move along wave

C4.3 Phase on standing wave

In phase: even nr of nodes between - within 1 loop

Anti phase/out of: odd nr of nodes between

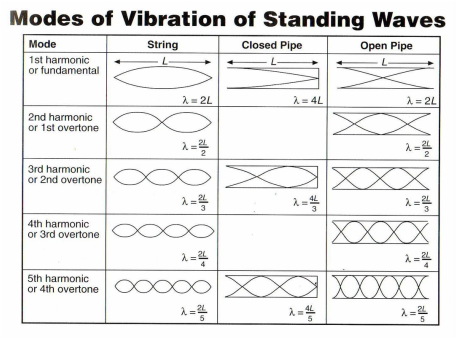
C4.4 Boundaries

Form on strings, in pipes:

nr of nodes depends on: f of producing wave, boundary conditions:
- 2 fixed ends, 2 loose ends, 1free1loose ends

At open end: always antinode
Closed end: alway node

Pipe: longitudinal waves when blowing in an open end; can be 2 fixed ends, 2 loose ends, 1free1loose ends
Guitar: 2x fixed

fixfix: At natural frequency: ^nλ/₂ nodes; ^nλ/₄ full waves.

C4.5 Open closed pipe λ

NOT IN FORMULA BOOKLET — REMEMBERRRR!!!!!
Open-closed: λ = ^4L/_n - n=1,3,5… (n=nr of nodes=harm)

Open-open: λ = ^2L/_n - n=1,2,3…(n=nr of nodes = harmonic)

Closed-closed; λ = ^2L/_n - n=1,2,3… (n=nr of rondjes=harm)

v = fλ

C4.6 Free oscillations vs forced

Free: no transfer of energy to/from surrounding; no external forces on it, vibrates naturally, only internal forces. Free vibration always oscillates at natural/resonant frequency.

Forced: to sustain oscillations in SHM; periodic F must be applied to replace lost energy in damping by resistive forces (friction, drag). Driving force can change frequency of oscillator.

C4.7 Resonance

driving frequency: f - forced
natural frequenct: f_o - f os oscillation when oscillating freely

Resonance = f = f_o → maximum amplitude

C4.8 Damping

Eventually, after driving force stops, all oscillators stop oscillating, as they are damped by external F (drag-friction) acting opposite to motion, reducing the E_k of the oscillator, and turning it into heat

Their amplitudes are decreased, until oscilator is at rest at equilibirum. f and λ are not changing!!

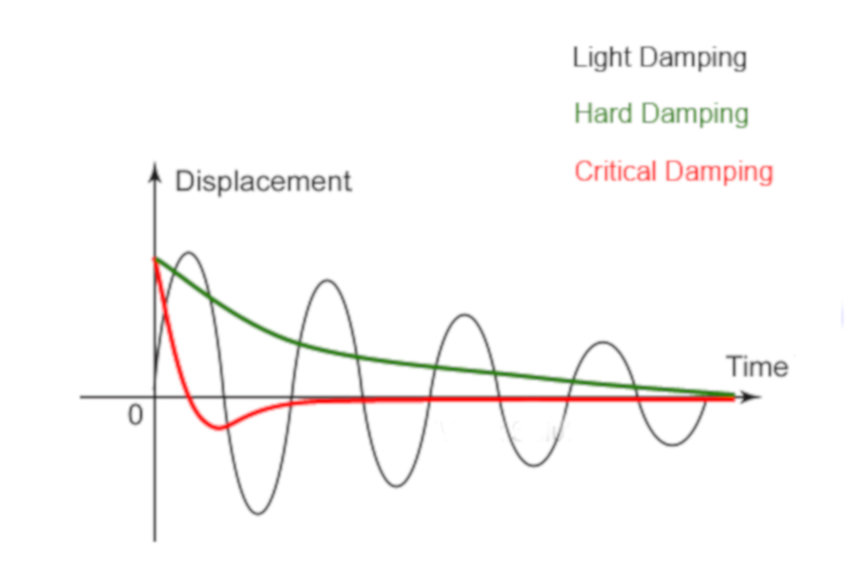
C4.9 Types of damping

Light damping: gradual, exponential decay of A, makes oscill.

Critical damping: return to rest in shortest possible time, no oscillation;

Heavy damping: large resitance; takes ages to go to x=0; door damp

What is a wave?

A disturbance that can transfer energy without transferring matter as a whole

Longitudinal wave

A type of wave, where the oscillations occur parallel to the direction of energy transfer.

Compression

Areas of high pressure due to particles being close together

Rarefactions

Areas of low pressure due to particles being spread apart

Transverse waves

A type of wave, where oscillations occur perpendicular to the direction of energy transfer.

Examples of longitudinal waves

Sound waves

Examples of transverse waves

Electromagnetic waves and water waves

Displacement

Distance of a point on the wave from its equilibrium position

Amplitude

The maximum displacement from the equilibrium position

Wavelength

The distance between two consecutive points that are in phase

Period

Time taken for one complete oscillation

Frequency

Number of complete oscillations per second

In phase

When two points have a phase difference of 0 or 2pi

Antiphase

When two points have a phase difference of pi

Path difference

The difference in distance travelled by two waves to reach a specific point.

When does polarisation occur?

Polarisation occurs when oscillations are confined to a single plane.

What are the applications of polarisation?

• Polaroid sunglasses reduce glare by blocking horizontally polarised light.

• Antennas must be aligned to the plane of the wave

Why can’t longitudinal waves be polarised?

Their oscillations are along the direction of travel, so there's no perpendicular direction to filter.

What is the principle of superposition?

When two or more waves meet at a point, the total displacement is the vector sum of the individual displacements.

Constructive interference

Waves in phase; amplitudes add.

Destructive interference

Waves in anti-phase; amplitudes subtract.

The conditions for sustained interference

• Waves must be coherent

• Similar amplitude and same type

What does coherent mean?

Same frequency and constant phase difference

How is a stationary wave formed?

When two waves of identical frequency, amplitude, and speed move in opposite directions and interfere with each other

What are nodes?

Points of zero displacement in a stationary wave.

What are antinodes?

Points of maximum amplitude in a standing wave.

What are the features of a stationary wave?

There is no net energy transfer

Fundamental harmonic

The fundamental harmonic is the simplest standing wave with only one antinode and two nodes

When does resonance occur?

Resonance occurs when the frequency of a vibration matches the natural frequency of an object, causing the object to vibrate

Where is resonance used?

In musical instruments and in measuring the speed of sound