D1: Graph Theory + Definitions

graph

a mathematical model that consists of arcs/edges and nodes/vertices

network

a weighted graph i.e. a graph with numbers associated to its edges

vertex set

list of all the vertices in a given graph

edge set

a list of all the edges in a given graph

subgraph

A part of the original graph (vertices and edges also belong to original graph)

degree/valency/order of a vertex

number of edges incident to it

pendant

a node of degree one

isolated

a node of degree zero

walk

a route through a graph along edges from one vertex to the next

path

a walk with no repeated vertices

trail

a walk with no repeated edges

cycle

a walk in which the end vertex is the same as the start vertex and no other vertex is visited more than once (or a trail that starts and ends at the same vertex)

Hamiltonian cycle

A cycle that visits every vertex of a graph

two vertices are connected if...

...there is a path between them

a graph is connected if...

...all its vertices are connected

connected components

subgraphs that are connected

loop

an edge that starts and finishes at the same vertex

how does a loop affect the degree of a vertex

the vertex the loop originates from has a degree of 2 and not 1 due to it. this is because the loop is incident at the vertex twice.

simple graph

a graph with no loops or multiple edges between vertices

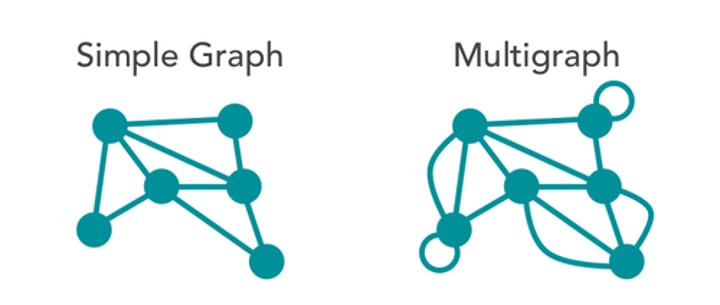
directed graph (digraph)

a graph with a direction associated with the edges

Euler's handshaking lemma

in any undirected graph, the sum of the degrees of the vertices is equal to 2x the number of edges. As a consequence, the sum of the degrees must always be even.

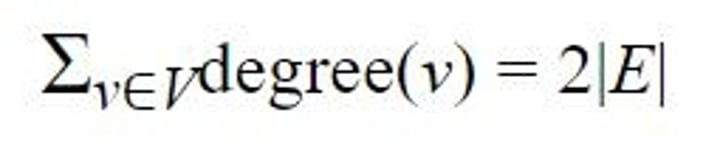
how is euler's handshaking lemma used?

to determine whether a graph can exist - if the sum of the degrees is odd, that implies the number of edges is not an integer which is impossible

in any undirected graph there must be...

an even amount of vertices with an odd degree

tree

a simple connected graph with no loops or circuits

spanning tree

a tree which includes all the vertices of the graph

complete graph

a graph where every vertex is directly connected by a single edge to each and every other vertex

how is a complete graph denoted?

Kₙ where n is the number of vertices in the graph

isomorphic graphs

graphs that show the same information but are drawn differently

what makes two graphs isomorphic?

- they have the same number of vertices with the same degree

- the vertices are connected in the same way

- the vertices may have different labels as they are not the same graph but still an equivalence

adjacency matrix

a matrix that provides information about the connections between the vertices in a graph

what should each entry be for the adjacency matrix of an unweighted graph?

the number of arcs joining two points

describe how a loop from point A to A is depicted in an adjacency matrix for an undirected graph

it counts as two arcs as they can go in either direction ∴ the entry would be 2

(it is a similar principle to how e.g. AB could be 1 ∴ BA would also be 1)

distance matrix

the matrix associated with a weighted graph

what should each entry be for a distance matrix?

the weight of the arc joining two nodes

what if there are multiple arcs joining two vertices in a weighted graph? what should the entry be in the distance matrix + why?

the smallest weight; this is because when an algorithm is applied to the matrix to e.g. find the shortest route, the least value is desired.

minimum spanning tree (MST)

a spanning tree such that the total length of its edges is as small as possible

what is another name for a minimum spanning tree?

minimum connector

Eulerian circuit

A trail that starts and ends at the same vertex and traverse every arc no more than once

Semi-eulerian circuit

A trail that traverses every arc no more than once, but doesn’t start and end at the same vertex

Traits of a Eulerian graph

• all vertices are even

• connected

• contains a Eulerian circuit

Traits of a semi-Eulerian graph

• exactly two vertices are odd

• connected

• contains a semi-Eulerian circuit