Engng Math 145 Matrices

Coefficient and Augmented Matrix

Augmented is like coefficient but with coefficients to right of equal sign too.

Row echelon form

1. All zero rows are at bottom

2. In each non-zero row, each leading entry is in a column to the left of any leading entries below it.

Reducing to REF is called Guassian elimination.

Elementary row operations

Only do one ERO at a time.

• Multiply rows by constant

• Swapping rows

• Adding or subtracting rows from each other

Parameter variables

Used when REF matrix has a row with >1 non-zero elements OR zero row equal to zero, so infinitely many solutions.

Process: All non-pivot variables must be set to a parameter variable (s, t, u, v), and pivot variables must be solved for in terms of the parameter variables.

eg. 2x + 3y = 4 → x = 2 - (3s) / 2, where y = s

No real solutions & infinitely many solutions

Has zero row equal to non-zero. eg. 0 = 5

Has zero row equal to zero. eg. 0 = 0. This is because some rows are scalar multiples of each other.

Reduced row echelon form

1. Is in REF

2. Every non-zero row’s leading entry is a 1 and there are no other non-zero entries in the leading entry’s column.

Reducing to RREF is called Gauss-Jordan elimination.

Diagonal & scalar matrix

Diagonal matrix is square matrix in which all non-diagonal entries are 0.

Scalar matrix is diagonal matrix where all diagonal entries are equal to each other, but not 0.

Upper and lower triangular matrix

Square matrix where all entries below/above diagonal are zero (opposite to it’s name).

n x n Identity matrix

Square matrix with dimension n.

All non-diagonal entries are zero and diagonal entries are 1.

Mathematically equal to 1.

Equal matrices and zero matrices

Same size and all entries equal.

Zero matrix has only zero entries.

Matrix addition/subtraction and scalar multiplication

Can add matrices if same size arithmetically.

For subtraction use A - B = A + (-1)B

Multiply each entry by scalar.

Matrix multiplication

Dot multiply rows of first matrix with columns of second matrix.

Order matters.

Transpose matrix and symmetry

A^T : Rotate A clockwise 90^o, then mirror horizontally.

Symmetric when A = A^T

Transpose rules

(A + B)^T = A^T + B^T

(A^T)^T = A

(AB)^T = B^TA^T

(kA)^T = kA^T

(A^r)^T = (A^T)^r

For every square matrix A, A + A^T is symmetric.

For any matrix A, AA^T and A^TA are symmetric.

Pivot variables

Pivot variables are the variables with leading elements attached to them when matrix is in REF. eg:

2x + 3y + z = 5

0x + y + 2z = 1 (this matrix has infinitely many solutions)

0x + 0y + 0z = 0

y & x are pivot variables.

Determinants

Defined for square matrices

Denoted as det(A) or |A|

Det of 1×1

= a

Det of 2×2

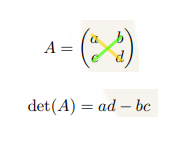
Det of 3×3

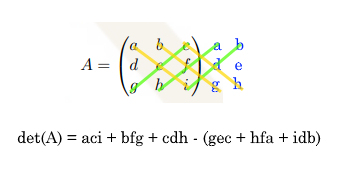
Minor determinant

M_ij of A is det(A), but with i^th row & j^th column removed

Co-factors of a matrix

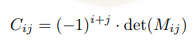
Determinants using cofactors

A = [a_ij], where n > 2:

det(A) = a_i1C_i1 + … + a_inC_in (calculate by rows)

det(A) = a_1jC_1j + … + a_njC_nj (calculate by columns)

• if first row has more zeros than first col, choose row formula. vice versa.

• a is term of matrix, C is cofactor

Determinant properties

Where A, B = nxn matrices & k is constant

• det(A^T) = det(A)

• det(A^-1) = 1 / det(A)

• det(kA) = kⁿ det(A)

• det(AB) = det(A) det(B)

• If A has zero row/column; det(A) = 0

• If A has 2 identical rows/cols; det(A) = 0

Note: det(A+B) is NOT equal to det(A) + det(B)

EROs:

• Swapping 2 rows/cols of A; det(A) = -det(new)

• Multiplying row/col of A by k; det(A) = 1/k det(new)

• Adding a multiple of a row/col of A to another row/col; det(A) = det(new)

Determinant of triangular matrix

det(A_tri) = product of the entries on its main diagonal

used for “solve via properties”

Inverse of a matrix

AA^-1 = A^-1A = I, where I is nxn identity matrix

If A^-1 exists → A is called invertible/non-singular.

Properties of inverse matrix

Where A & B are invertible, c is constant, n is positive integer, r & s are integers.

• If A = invertible matrix, then A^-1 only has one solution

• (A^-1)^-1 = A

• (cA)^-1 = (1/c) A^-1

• (A^T)^-1 = (A^-1)^T

• (AB)^-1 = B^-1A^-1

• A^-n = (A^-1)ⁿ = (Aⁿ)^-1

• A^rA^s = A^r+s

• (A^r)^s = A^rs

Requirement for matrix to be invertible

nxn matrix A is invertible if and only if det(A) ≠ 0.

Inverse of 2×2 matrix

ad - bc is det(A)

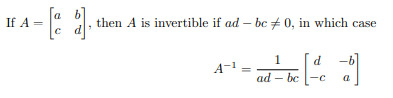
Inverse of nxn matrix

For an invertible matrix A,

A^-1 = 1/det(A) * adj(A)

• picture of adjugate of A →

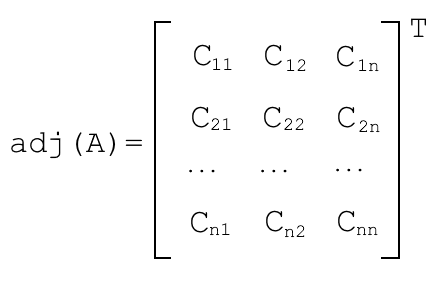
Determining inverse with EROs (Gauss-Jordan Method)

Let A be nxn matrix. If sequence of EROs transforms A to I, then same sequence of EROs transforms I to A^-1.

Solving Ax = b

Ax = b → A^-1Ax = A^-1b → Ix = A^-1b → x = A^-1b

where A is nxn coefficient matrix, x ∈ {x₁, …, x_n}, b is constant terms of system.

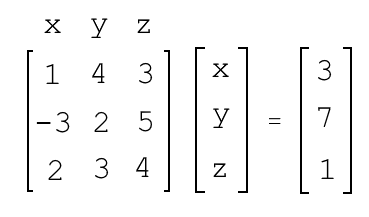
Fundamental theorem of invertible matrices

Let A=nxn matrix. The following statements are equivalent:

• A is invertible (det(A)≠0)

• Ax = b has unique solution for every b in ℝⁿ

• Ax = 0 has only the trivial solution

• Reduced row echelon form of A is I_n

Cramer’s Rule

For Ax = b, then

x_k = |A_k| / |A|, for k ∈ {1,2,…,n},

where A_k is A but k^th col is replaced by b.

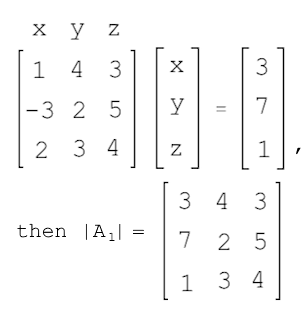
Picking method for question

Determinants:

• Formula: 1×1, 2×2 or 3×3 matrices

• Co-factors: matrix has row/col with many zeros

• Properties: “default” method for > 3×3 matrices

Inverses:

• Formula: 2×2 matrix

• Adjoint/co-factors: only when specified in question

• Gauss-Jordan: “default” method for > 2×2 matrices

Solving linear systems:

• Gauss/Gauss-Jordan: “default” method

• x = A^-1b: if inverse is known

• Cramer’s rule: if determinants are known