Week 2 Lecture 2 - Closure Properties of Regular Languages

Give the name for the property where a language is regular because there is an FSA that accepts it.

Closure

Draw the languages:
L₁ = {aⁿ | n >= 2} and L₂ = {ab^ma | m >= 0}

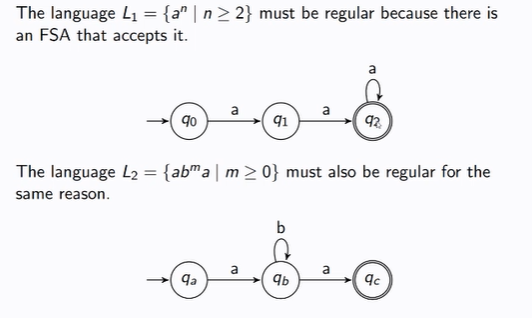
For regular languages L₁ and L₂, is L₁ U L₂ regular?

Yes

Give the drawing of L₁ U L₂
Method not using λ transitions
L₁ = {a}∗{b} and L₂ = {aa, ab}

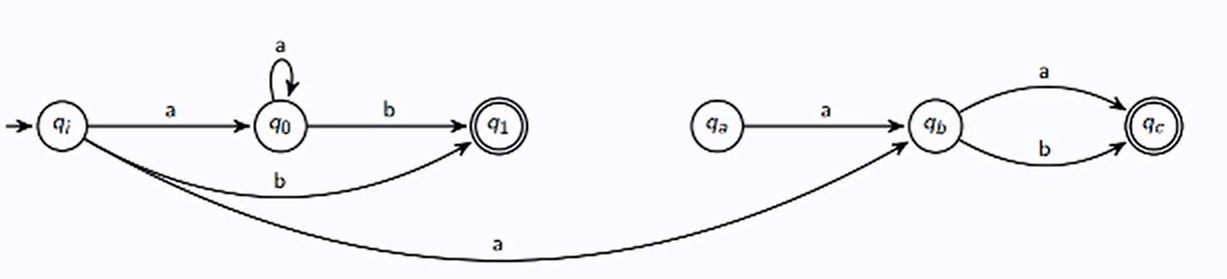
Give the drawing of L₁ U L₂
Method using λ transitions
L₁ = {a}∗{b} and L₂ = {aa, ab}

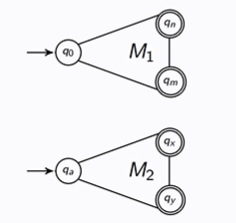
Draw the generalised pattern for M₁ U M₂

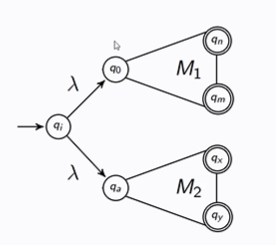
For regular languages L₁ and L₂, is L₁L₂ regular?

Yes

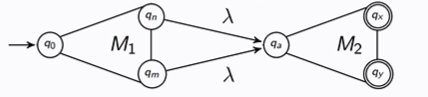
Draw the generalised pattern for M₁M₂

Prove by induction that if L_1, … , L_n is a regular language, where n >= 1, then L₁….L_n is also a regular language

Base case: n = 1
In this case, L₁….L_n = L₁ and L₁ is regular by definition.

Inductive step:

L₁….L_{n =} L₁….L_n-1L_n
L_n is a regular language by assumption and L₁….L_n-1 is a regular language by inductive hypothesis. So L₁….L_n must be a regular language.

What is L^*? And is it a regular language

Yes

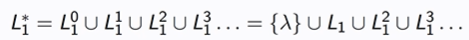
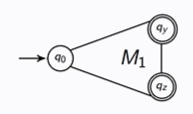
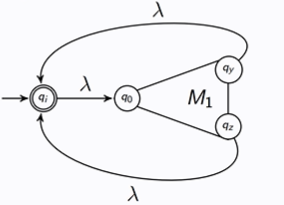
Given M₁ is an FSA that accepts L₁, what is the FSA that accepts L₁*?

The new initial state must be final or λ is not accepted.

What is the complement of L and is it a regular language?

Σ^* - L

Yes

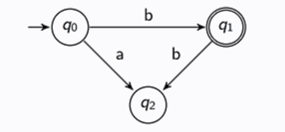
Consider the DFA M = (Q, Σ, δ, i, F ) such that L = L(M)

What is the FSA that accepts the complement? Give the steps

1) Complete M so that it has transitions from every state for every symbol. This is done by adding a junk state.
2) Invert the final + non-final states

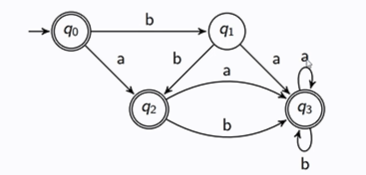
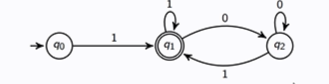
Consider the language L which consists of all binary strings that start and end in a 1. Construct the FSA that accepts the complement:

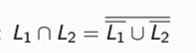
Using de Morgans law, prove this is regular:

Show the construction of closure under intersection using:

Using these 2 languages L₁ and L₂, construct the FSA that accepts the intersection

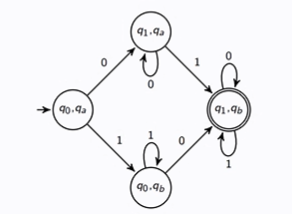
Prove that if L and M are regular languages, so is L - M