AP calc graphs to memorize
Studied by 0 people
Knowt Play
Learn
Practice Test
Spaced Repetition
Match
Flashcards1/19
Earn XP
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
20 Terms
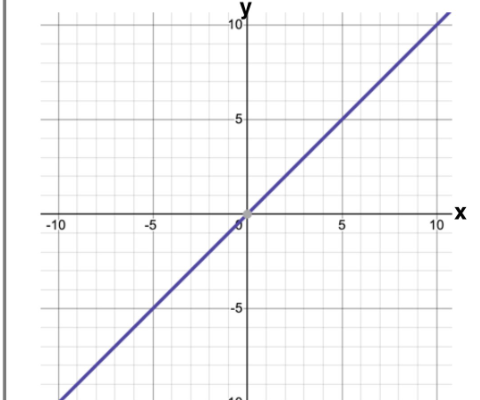
linear function
f(x) = x
D: xeR
R: yeR
x-int + y-int: (0,0)
x→ -∞, y→ -∞
x→ ∞, y→ ∞
origin symmetry
quadratic function
f(x) =
D:
R:
x-int
x→ -∞, y→
x→ ∞, y→
symmetry
asymptote
cubic function
f(x) =
D:
R:
x-int
x→ -∞, y→
x→ ∞, y→
symmetry
asymptote
cube root function
f(x) =
D:
R:
x-int
x→ -∞, y→
x→ ∞, y→
symmetry
asymptote
square root function
f(x) =
D:
R:
x-int
x→ -∞, y→
x→ ∞, y→
symmetry
asymptote
logarithmic function
f(x) = ln x
D:
R:
x-int
x→ -∞, y→
x→ ∞, y→
symmetry
asymptote
exponential function
f(x) = e^x
D:xeR
R:y>0
y-int: (0,1)
x→ -∞, y→ 0
x→ ∞, y→ infinity
HA: y=0
reciprocal function / inverse function
f(x) = 1/x
D:xeR
R: -1>y>1
no intercept
x→ -∞, y→ 0
x→ ∞, y→ 0
origin symmetry
VA: x=0
HA: y=0
f(x) = 1/x²
D:
R:
x-int
x→ -∞, y→
x→ ∞, y→
symmetry
asymptote
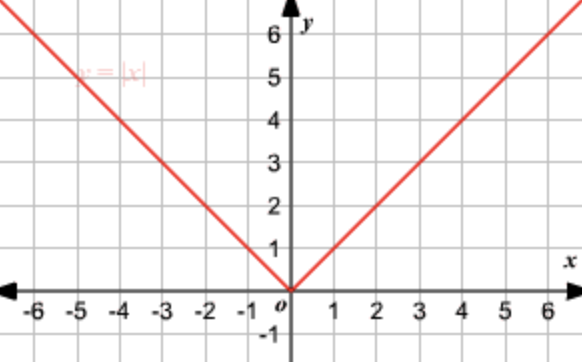
absolute value function
f(x) = |x|
D: xeR
R: y>0, yeR
x-int and y-int: (0,0)
x→ -∞, y→ ∞
x→ ∞, y→∞
y-axis symmetry
trigonometric sine function
f(x) = sin x
D: xeR
R: [-1, 1]
x-int: (0,0), pi*n (neZ)
y-int: (0,0)
x→ -∞, y→
x→ ∞, y→
origin symmetry
![<p>f(x) = sin x</p><p>D: xeR<br>R: [-1, 1]</p><p>x-int: (0,0), pi*n (neZ)<br>y-int: (0,0)</p><p>x→ -∞, y→ <br>x→ ∞, y→</p><p>origin symmetry</p>](https://knowt-user-attachments.s3.amazonaws.com/e6ac08c0-c767-40d8-b3d7-18267da7adf4.png)
trigonometric cosine function
f(x) = cos x
D: xeR
R: [-1, 1]
x-int: pi/2 + pi*n, neZ
y-int: (0,1)
x→ -∞, y→
x→ ∞, y→
y-axis symmetry
![<p>f(x) = cos x</p><p>D: xeR<br>R: [-1, 1]</p><p>x-int: pi/2 + pi*n, neZ<br>y-int: (0,1)</p><p>x→ -∞, y→ <br>x→ ∞, y→</p><p>y-axis symmetry</p>](https://knowt-user-attachments.s3.amazonaws.com/35fdeea9-694d-45b1-a4ab-349658673836.png)
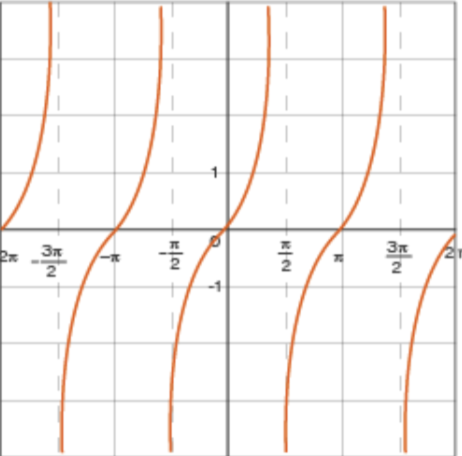
trigonometric tangent function
f(x) = tan x
d: x ≠ pi/2 (2n+1), neZ, xeR
R: yeR
x-int and y-int: (0,0)
x→ -∞, y→
x→ ∞, y→
origin symmetry
VA: pi n, neZ
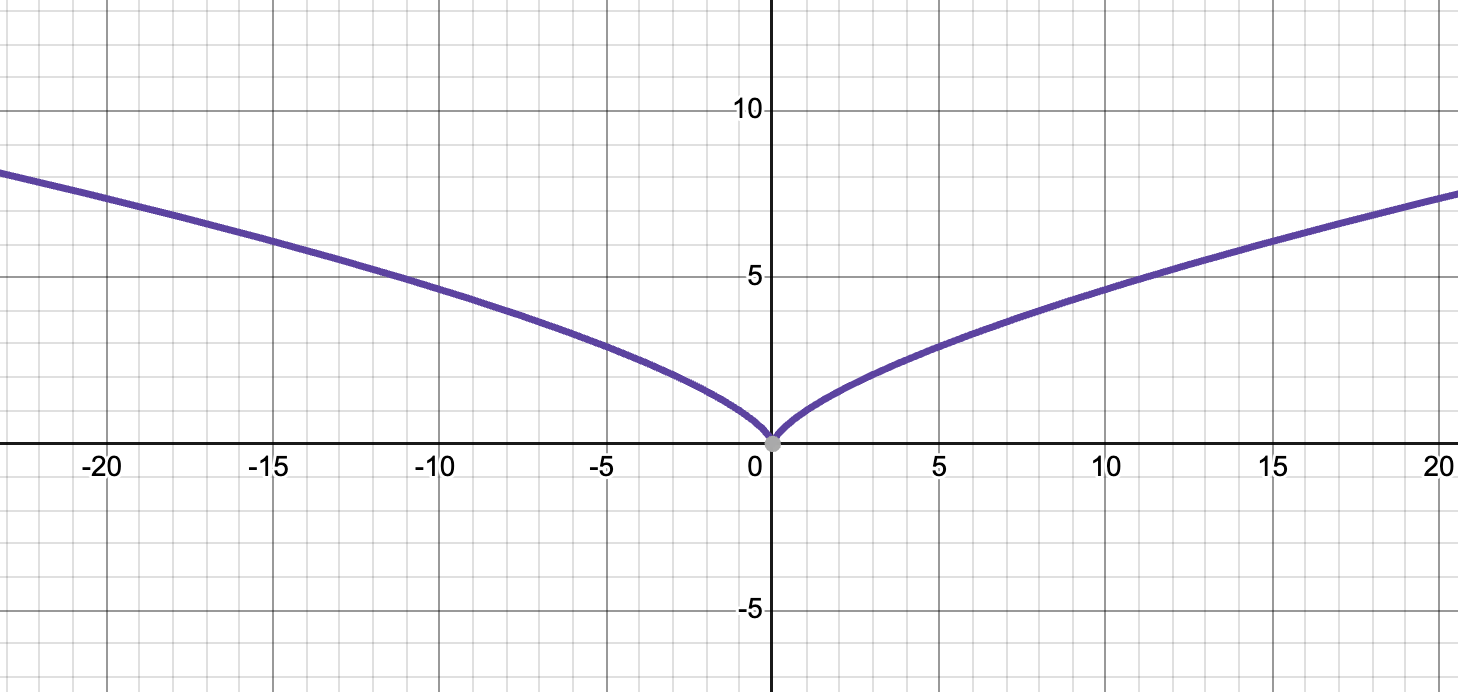
f(x) = x²/³
d: xeR
R: y>0, yeR
x-int/y-int: (0,0)
x→ -∞, y→ ∞
x→ ∞, y→ ∞
y-axis symmetry
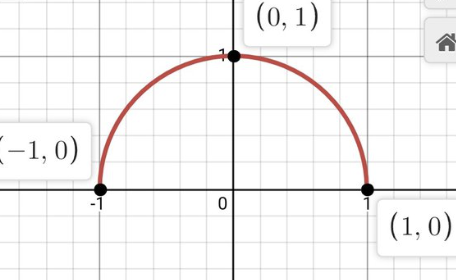
semicircle function
f(x) = \sqrt{r² - x²}
D: -r <x< r
R: 0< y < r
x-int: (-r,0) and (r,0)
y-int: (0,r)
x→ -∞, y→
x→ ∞, y→
y-axis symmetry
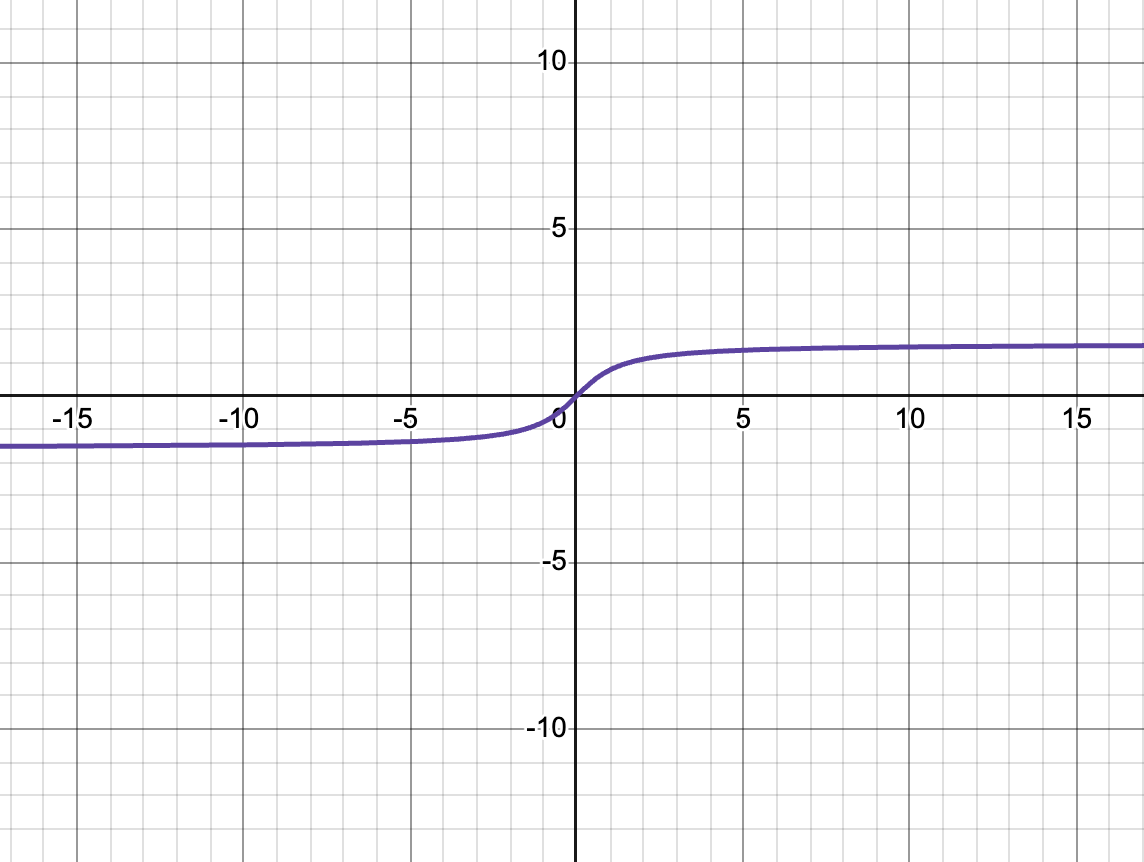
inverse trig function (tan)
f(x) = Arc tan x
D; xeR
R: (-pi/2, pi/2)
x-int/y-int: (0,0)
x→ -∞, y→ -pi/2
x→ ∞, y→ pi/2
origin symmetry
HA at y = -pi/2 and pi/2
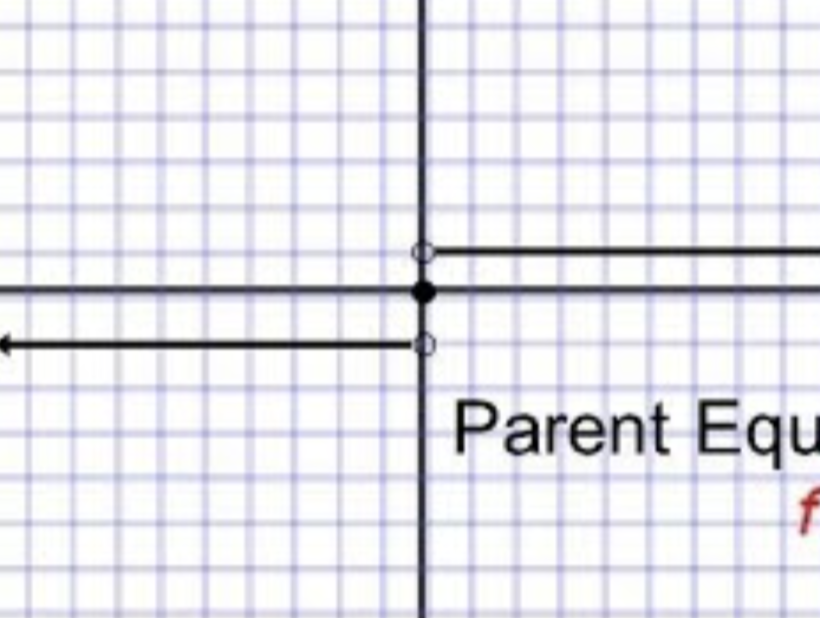
sign / signum function
f(x) = |x| / x
D: xeR (-∞, ∞)
R: y = {-1, 0, 1}
x-int & y-int: (0,0)
x→ -∞, y→ ?
x→ ∞, y→ ?
symmetry?
asymptote?
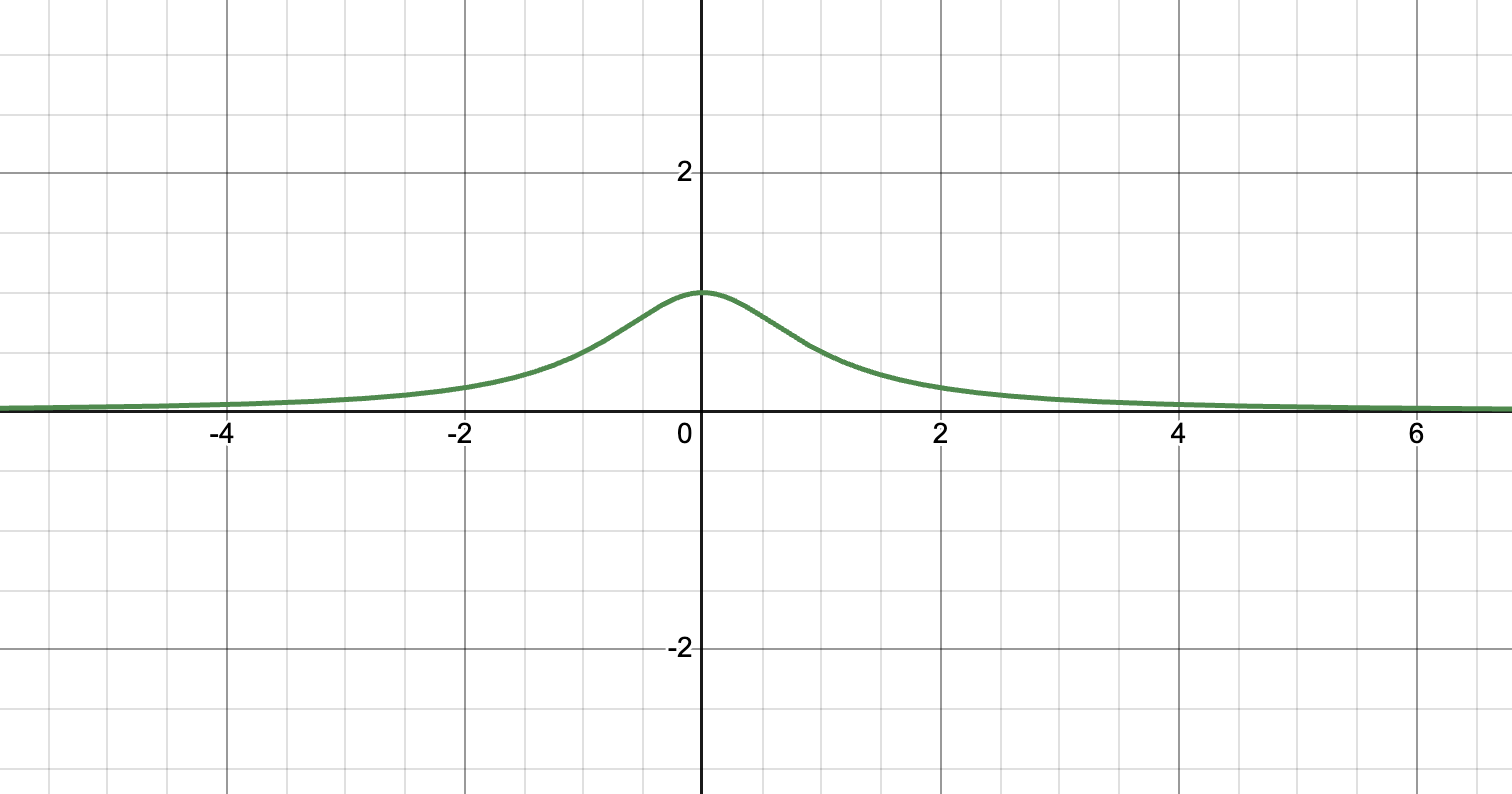
f(x) = 1/ (x²+1)
D: x ≠ 0, xeR
R: 0< y< 1, yeR
y-int: (0,1)
x→ -∞, y→ 0
x→ ∞, y→ 0
y-axis symmetry
HA: y = 0
hyperbolic cosine function
f(x) = ½ (e^x + e^-x) = cosh x
D: xeR
R: {y|y>1, yeR} [1, ∞)
y-int: (0,1)
x→ -∞, y→ ∞
x→ ∞, y→ ∞
y-axis symmetry
step function / greatest integer function
f(x) = [| x |]
D: xeR
R: yeZ (integers)
x-int: (x,0) when 0 < x < 1
y-int: (0,0)
x→ -∞, y→ ?
x→ ∞, y→ ?