DISCRETE MATH

GRAPH THEORY

Is a branch of discrete mathematics that studies graphs, which are mathematical structures used to model pairwise relations between objects.

graph

consists of vertices (also called nodes) and edges (also called links) that connect pairs of vertices.

Leonhard Euler

Created the Graph Theory

Undirected Graph

Edges have no direction, connects two vertices symmetrically

Directed Graph

Also known as Digraph, edges gave a direction and indicated by arrows, Showing a relation from one vertex to another

Vertex

Also known as a node, is the fundamental point or unit of a graph, representing an object or entity

Edge

also known as link, a line that connects two vertices in a graph, may represent a relationship, intersection, or connection.

Weighted Edge

Edge that is associated with a numerical value

Unweighted Edge

An edge without any value

Degree of a Vertex

No. of edges incident to a vertex

In-Degree

Number of edges directed towards a vertex

Out-degree

Number of edges directed from a vertex

Path

Also known as Simple , a |_| where no vertices are repeated

Cycle

A path that starts and ends at the same vertex, forming a loop

Connected Graph

A graph where there is a path between every pair of vertices

Disconnected Graph

A graph where some vertices are not connected by any path

Subgraph

A graph from a subset of vertices and edges of another graph

Tree

A special type of graph that is connected and acyclic/no cycles

rooted tree

a tree where one vertex is designated as the foot

Complete Graph

A graph in which every pair of distinct vertices is connected by a unique edge

Bipartite Graph

A graph whose vertices can be divided into two disjoint sets such that no vertices within the same set are adjacent

Graph Isomorphism

Two graphs are isomorphic if one can be transformed into the other by renaming vertices without altering the structure of their connections

Network

Graph with weight function of numbers

Walks

also known as edge train or chain, defined as a finite alternating sequence of vertices and edges starting and ending with vertices, such that each edge is incident with the verticies preceding and following it

No edge appears more then once in a walk

Correct

No vertex may appear more than once

Incorrect, a vertex may appear more than once

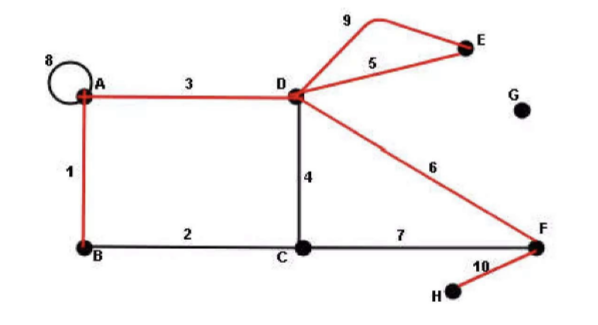
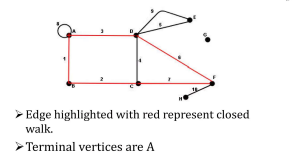
Closed Walk

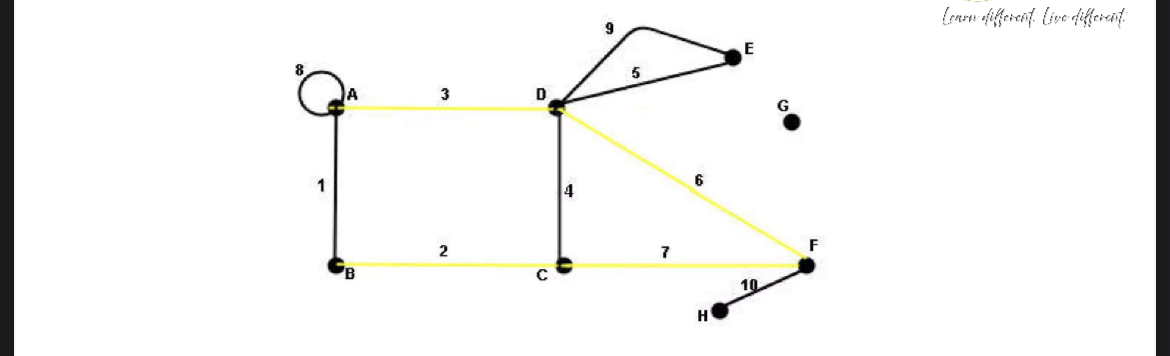
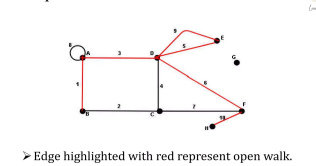
Open Walk

Path

An open walk in which no vertex appears more than once is called

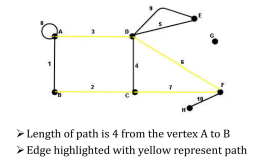
Length of Path

The number of edges in a path is called

Self-loop

Can be included in a walk but not in a path

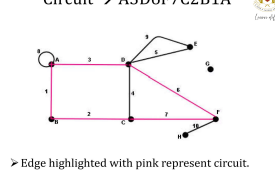
Circuit

A closed walk in which no vertex appears more than once except terminal vertices is called a

Path

Circuit

Acyclic

A graph is without cycles is

Connected

A graph is called |-| if for any couple vertices A and B there exists a path connecting A and B

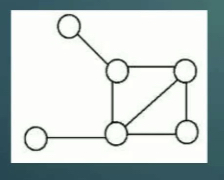
Simple Graph

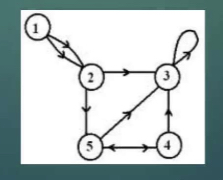
Directed Graph

Undirected Graph

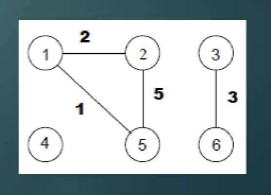
Weighted Graph

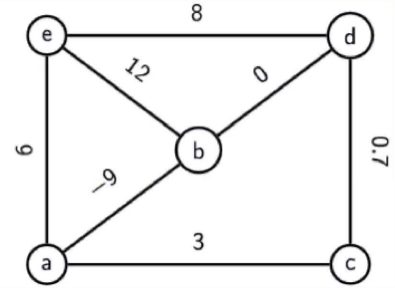
Closed Walk

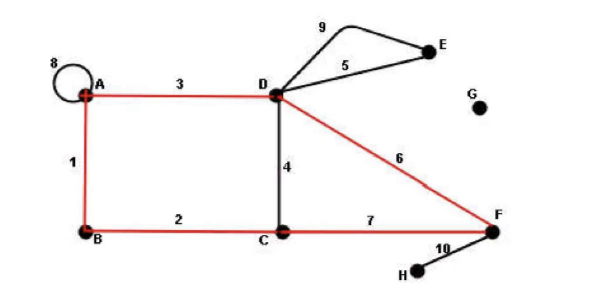
Open Walk