Further Applied Year 1 Definition

Sum of probabilities = …

1

Expected value E(X)

As no. Of observations increases, mean gets closer to expected value of discrete random variable.

E(X) = sum of [x P(X=x)]

E(X²) =…

Sum of [x² P(X=x)]

Var(X)

E(X²) - E(X)²

Comes from:

Var(X)= E( (X-E(X) )² )

Measure of spread. Larger it is, more likely X is to take values different to expected

E(aX+b)

aE(X) + b

Var(aX+b)

a²Var(X)

Poisson Distribution

Discrete. An infinite probability distribution.

Poisson distribution P(X=x)

(e^-lambda)(lambda^x)/x!, where X can only take positive integer values

Use when algebra involved

How must events occur for Poisson to be a good model

• independently

• One at a time (singly in time/space)

• At a constant average rate

What is lambda in poisson

Average number of times an event will occur in a single interval

If X~B(n,p), n is large and p is small, then it can be approximated by…

X~Po(np).

For binomial, mew=np and sigma²= np(1-p)

Variance, Var(X) for poisson is also…

Lambda

For poisson, if X~Po(lambda) and Y~Po(mew), then…

X+Y~Po(lambda+mew).

X and Y must both model events occurring within same interval of time or space

For poisson, P(both X and Y are greater than 2) =…

P(X>2) x P(Y>2)

If mean ≈ variance,

Poisson is suitable model to use

ALWAYS DEFINE X FIRST IN ANSWER!!!!

Difference between poisson and binomial

Poisson is unbounded whereas binomial is bounded by n

Hypothesis test for mean of poisson distribution

• Null, Ho: lambda = m is value of mean you assume to be true

• H1: tells you about value of mean if your assumption is shown to be wrong

For 2 tailed tests, probability needs to be as close to significance level as possible to be in CR, not just smaller!!!

Goodness of fit

Measuring how well an observed frequency distribution fits to a known distribution.

Ho: there’s no difference between observed and theoretical distribution

H1: there’s a difference between observed and theoretical distribution

Measure of goodness of fit equation

X² = sum of [Oi²/Ei] -N

The higher the value of X², the less similar the observed distribution is to theoretical distribution

Way to write goodness of fit hypotheses

• Ho: Observed data drawn from discrete uniform distribution

• H1: Observed data not drawn from discrete uniform distribution

No. of degrees of freedom (nu)

= no. of cells after combining - no. of constraints

No. of constraints

• total number for frequency is fixed so is a constraint

• If estimate for parameter is calculated then is a restriction, BUT if guessed by using sensible estimate from observation, then not.

Critical value at sig. level for Chi Squared

X²nu (sig. level) = ____

What if X² exceeds sig level

Sig level is probability that distribution exceeds critical value. E.g. X²2 (95%) =0.103 so P(X²2 > 0.103) = 95%

If X² exceeds critical value, its unlikely that null hypothesis is correct so reject it in favour of alternative.

HYPOTHESIS TEST FOR GOODNESS OF FIT IS ALWAYS ONE TAILED. CR IS ALWAYS SET OF VALUE GREATER THAN CRITICAL VALUE

Equation for estimating p

(Total no. of successes) /(no. of trials x N)

Where N is no. or observations.

Estimating for lambda for poisson equation

Total no. Of successes/ N

For last cell, Ei found by P(X>=r). DONT do this for when estimating for p

If asked how estimating p would affect test, say

whether conclusion changes, because nu would decrease so CR will change. Check if X² in CR or not after change

Contingency table hypotheses

• Ho: rows and columns are independent

• H1: rows and columns are not independent

Contingency table expected frequency

(Row total x column total) / grand total

If expected frequency in any column < 5, combine columns

Degrees of freedom for contingency tables

(No. Of rows - 1) x (no. Of columns - 1)

Momentum

Mass x velocity

Impulse

Change in momentum

Force x time

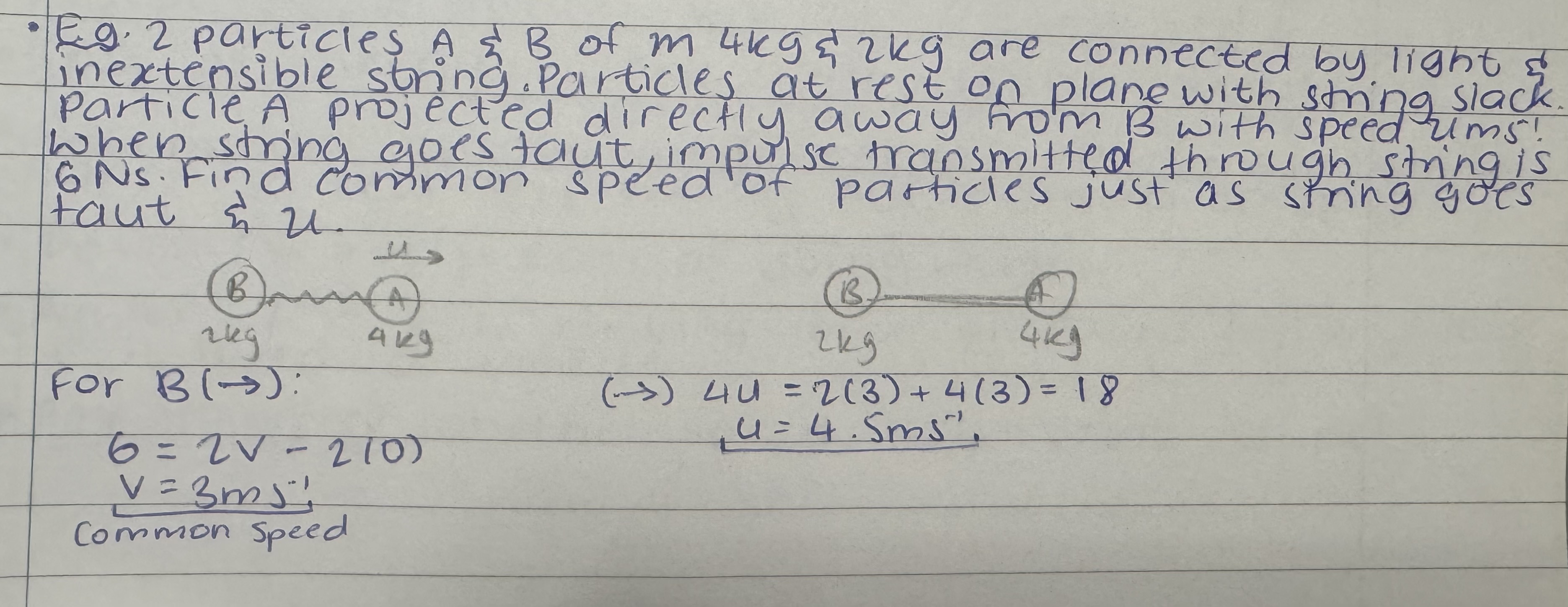
Work done

Component of force in direction of motion x distance moved in direction of force

Frictional Force F

Mew x R

Mew is frictional coefficient (0<=mew<=1)

R is normal reactant force

What does arcsine mean

Inverse of sine

Potential energy

Mgh

Work done by force which accelerates a particle horizontally

Change in KE

Decrease in PE =

Increase in KE for something falling

Total lost of energy =

KE lost - PE gained

Loss of energy =

Work done against friction

Principle of conservation of mechanical energy

When no external forces other than gravity do work on a particle during its motion, sum if particle’s KE and PE remain constant

Work energy principle

Change in total energy of a particle during its= work done on particle

Assumption usually made in mechanics questions

Resistive forces are constant. Probably not true in reality and changes with speed

Power

Rate of doing work

Power and force equation

Power = Fv, where F is driving force produced by engine and v is speed of vehicle

Only works when SPEED IS CONSTANT!!!!

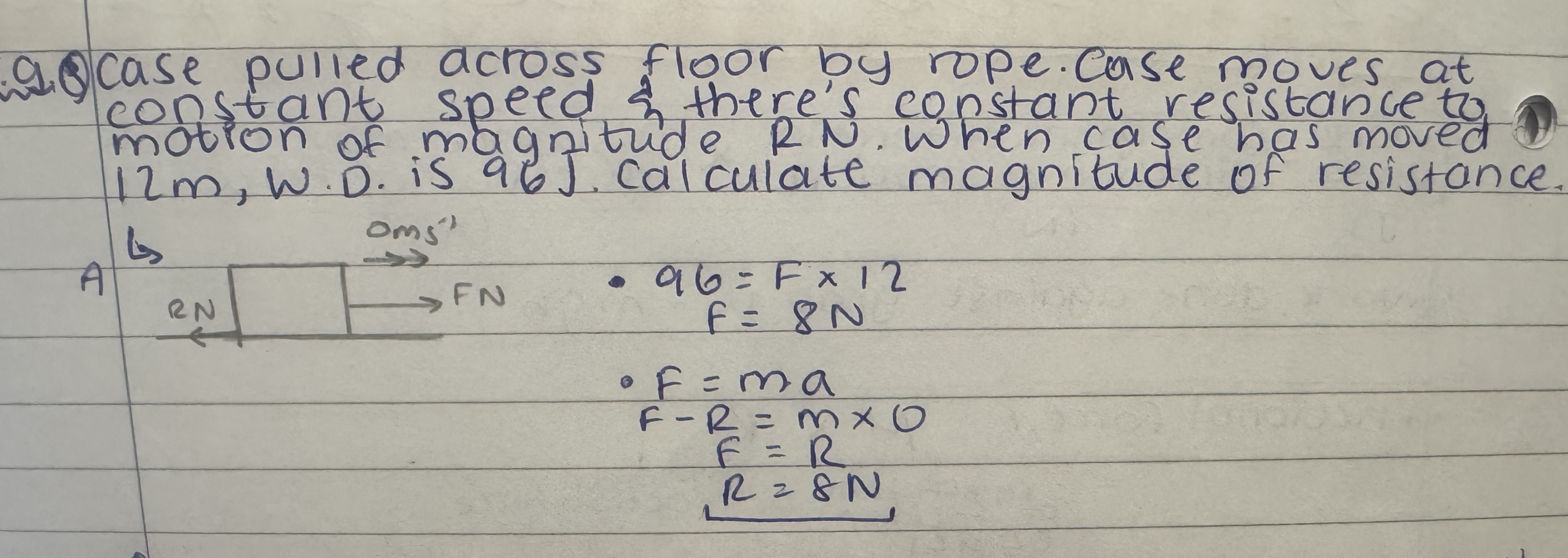
Newtons Law of restitution

e=relative speed of separation of particles/relative speed of approach of particles

0<=e<=1

In perfectly elastic collision, e=___

1

In perfectly inelastic collision, where particles coalesce, e=___

0

For direct collision of particle with smooth plane, e=___

Relative Speed of rebound/relative speed of approach

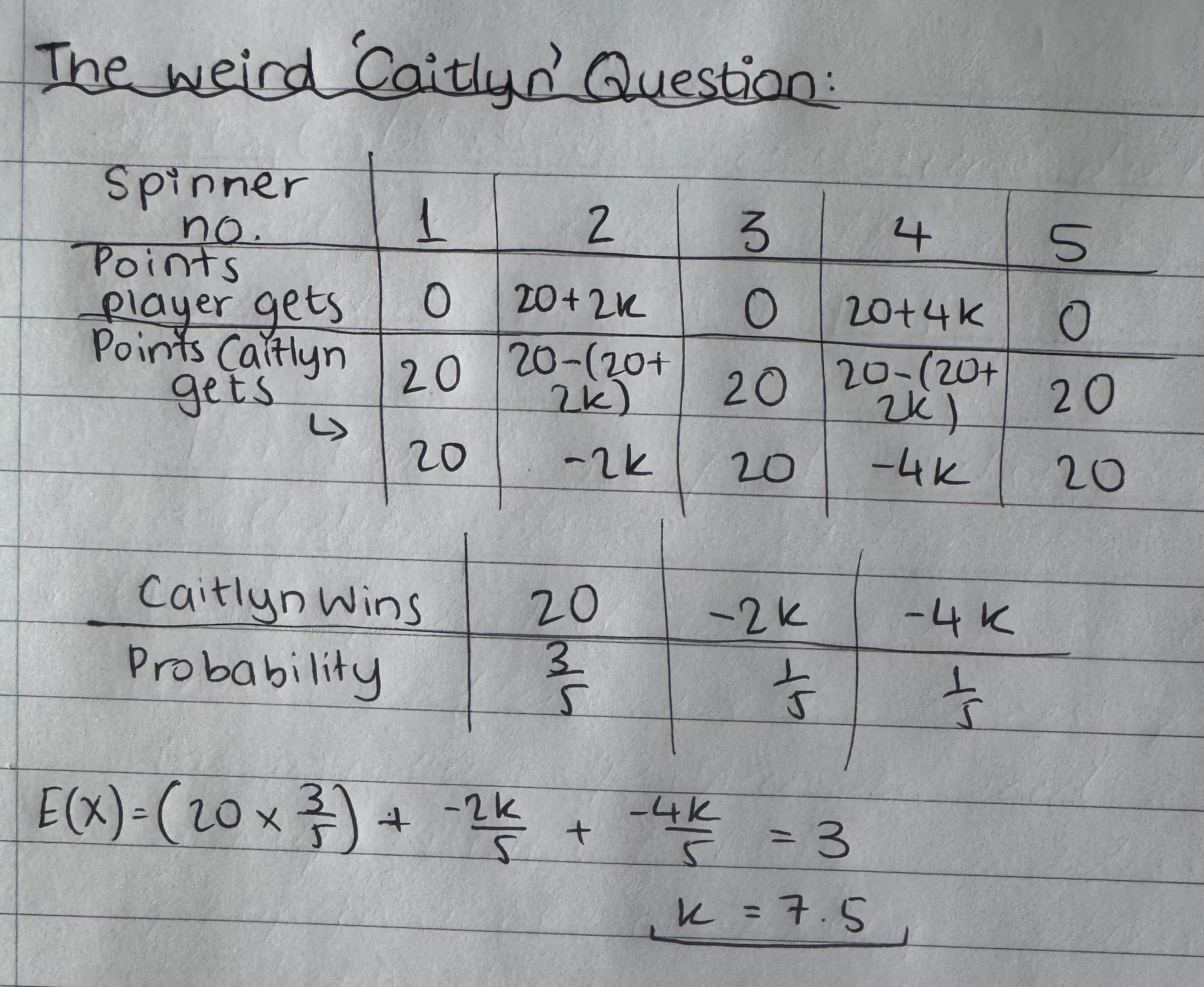
DONT FORGET TO STATE HYPOTHESES!!!!!!

Discrete uniform distribution if e.g. spinner is fair!!!

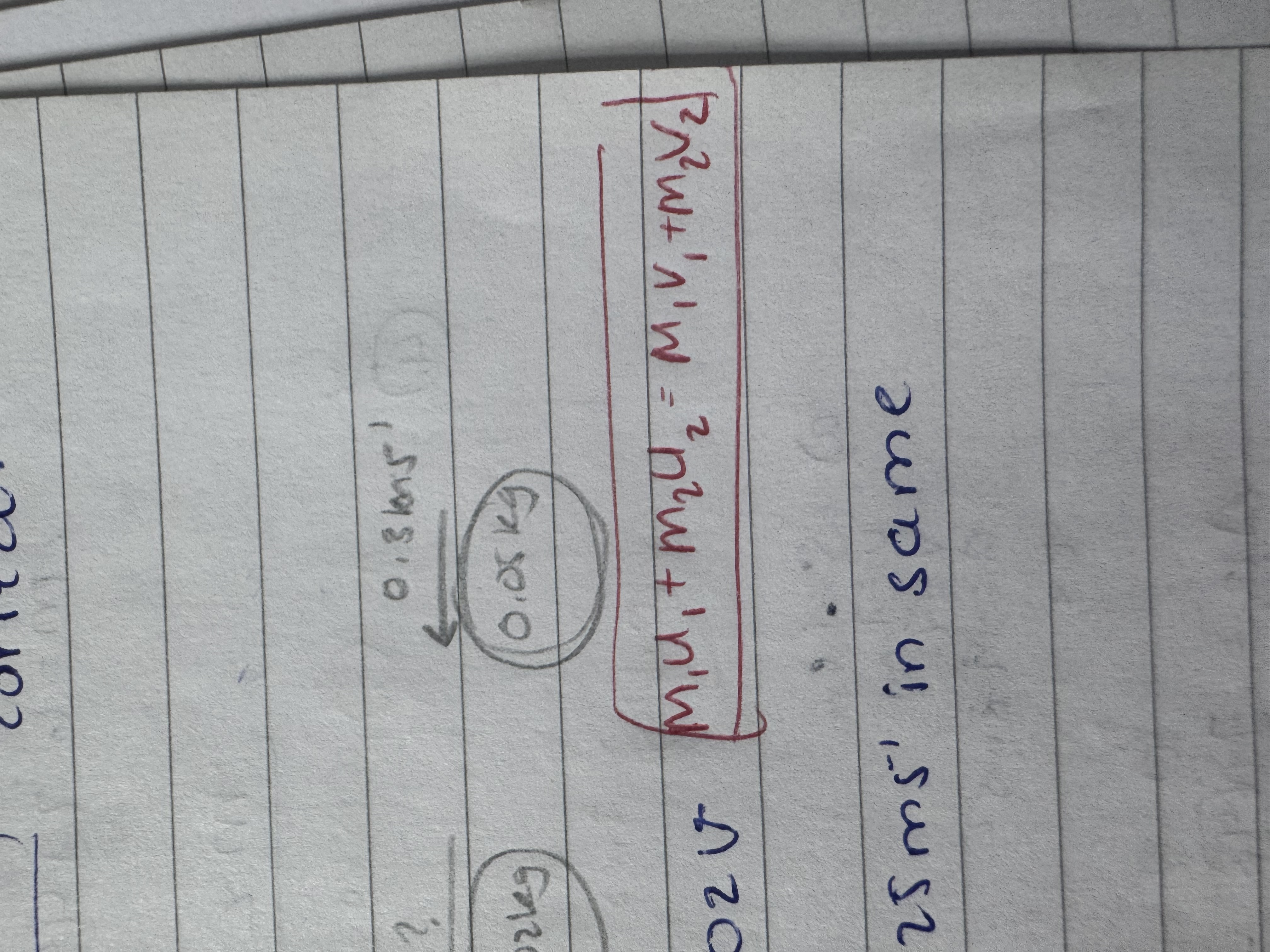
MUST STATE CONSERVATION OF MOMENTUM EQUATION BEFORE STARTING TO SOLVE!!!!

ALWAYS STATE WHICH EQUATION UR USING BEFORE USING AND ALSO WHY (e.g. momentum is same before and after etc)!!!!!

If question with drag and velocity, state drag is directly proportional to velocity!

STATE ALL LAWS, EQUATIONS, ETC BEFORE USING!!!!

For poisson, if P(X=0), most likely have to use poisson formula!!!!