linear final

adsfasdf

• How to tell if a matrix is one-to-one?

• It is one to one if it only has trivial solution / columns are linearly independent.

• How to tell if a matrix is onto?

• If there is a pivot in every row.

• If given radians remember:

• cos -sin
  sin cos

• If given T(es) = (points)

• then it is columns.

• If given T(es) = (equations)

• then those are rows.

If a matrix is a rectangle

then it is linearly dependent.

If a matrix has a zero vector

then linearly dependent

If a matrix has a column that is a multiple of another

then linearly dependent

• How to find the inverse of a 2x2 matrix?

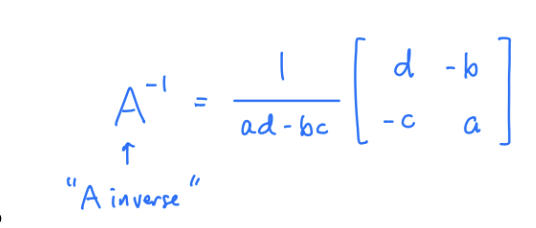
How to solve a linear system using an inverse?

• Take inverse and multiply it with b. Ax = b  -> A-1b = x

What happens if a triangle of zeroes below a diagonal?

• The product of the diagonal is the determinant

• Can also reduce to form the zero triangle to get the determinant

Cramer’s Rule

1. Find determinant

2. Replace the x,y,z columns with the RHS.

3. Find dx/d, dy/d, dz/d

Find determinants of matrices (up to 4 × 4) (3.1 and 3.2)

Show that a set of vectors is a basis for a vector space (4.3)

• An indexed set of vectors B in V is a basis for H if

• B is linearly independent (check)

• H spans B (find if it is invertible. If det 0, then it is invertible)

• To find basis for Nul A (Kernel)

• Solve Ax = 0

• Write solution in parametric vector form

• The vectors are are the solution

• Find a basis for Col A

• Reduce to echelon form

• Identify pivots

• The corresponding column in A itself form the basis

• To find a basis for Row A

• Reduce to echelon form

• The nonzero rows will be the basis.

• What is rank and nullity? 

• Rank = Number of vectors for basis of Col A

• Nullity = Number of vectors for basis of Nul A

• Rank Nullity Theorem = Rank + Nullity = # of columns in original A

Find the coordinates of a given vector v (in terms of a basis B) and its corresponding coordinate vector [v]B (4.4)

• Given coordinate vector and basis:

• take the coordinate vector, and distribute it to the basis

Find the coordinates of a given vector v (in terms of a basis B) and its corresponding coordinate vector [v]B (4.4)

• Given coordinate vector and basis:

• take the coordinate vector, and distribute it to the basis

• Find the coordinates of a given vector v (in terms of a basis B) and its corresponding coordinate vector [v]B (4.4)
  
  Given basis and x

• : Augment basis with x.

Find the coordinates of a given vector v (in terms of a basis B) and its corresponding coordinate vector [v]B (4.4)
Use coordinates to check that polynomials are linearly dependent

• Turn the polynomials into columns

• Augment with zero. 
  

  

Determine if a given vector is an eigenvector of a given matrix (5.1)

• If given vectors, multiply matrix with eigenvector

• If the answer is a multiple of the vector, then it is an evector.

• 

What happens if zero is along diagonal as an eigenvalue?

• Matrix is not invertible

Determine if a given number λ is an eigenvalue of a given matrix A (by analyzing A − λI) (5.1)

• Subtract matrix from the eigenvalue

• Augment with zero, and see if it is linearly independent. 

• If dependent, then it is an eigenvalue

• If asked for the corresponding eigenvectors

  • Find the weird form. That is the vector

Find the eigenvalues of a matrix (5.2).

• Subtract lambda from the matrix

• Find determinant and set equal to zero

• Factor to get eigenvalues.

Determine whether a given matrix is invertible based on its eigenvalues (5.2)

• A matrix A is invertible if and only if all of its eigenvalues are non-zero.

Diagonalize a matrix (up to 3 × 3) by finding a diagonal matrix D and a matrix P such that A = PDP^−1 (5.3). 

• To diagonalize a given matrix

  • Subtract diagonal by eigenvalues.

  • Find determinant 

  • Factor determinant, those are your eigenvalues

  • D = eigenvalues in diagonal

  • P = Find 3 linearly independent eigenvectors

    • Subtract matrix from eigenvalues, augment with zero.

    • Find weird form, that is the P.

Find the length of a vector (6.1).

• Find norm, sqrt(u^2 + v^2)

Normalize a vector:

• Find unit vector

Determine if two vectors are orthogonal

• Dot product, if zero, then orthogonal

Show that a given set of vectors is an orthogonal basis for a subspace of R^n (6.2)

Find if all are orthogonal, then check determinant and LI

Find the projection of a vector onto a subspace (6.3).

Find the distance between a vector and a subspace (6.3).