L2 - Robust estimation of multivariate location and scatter

How do practitioners often check for outliers?

What is the problem with this approach?

Multivariate outliers may not be extreme in any variable. Such outliers are called correlation outliers.

What is the idea for detecting correlation outliers?

What kind of problem does this lead to?

What are those methods?

Minimum covariance determinant (MCD) estimator

One-step reweighted estimator

What is the idea of the MCD estimator?

What is the geometric meaning of the determinant of the covariance matrix?

Geometrically, the determinant of the covariance matrix is proportional to the (hyper)volume

How do we denote the sample mean that uses observations from subset H?

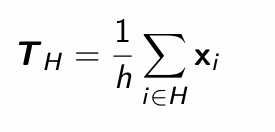
How do we denote the sample covariance matrix that uses observations from subset H?

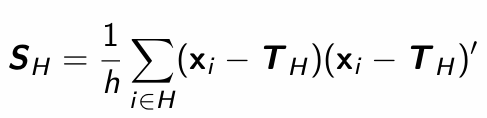
What is the objective function for finding HMCD?

What is the functional for the mean over a set A?

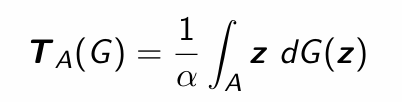
What is the functional for the covariance matrix over a set A?

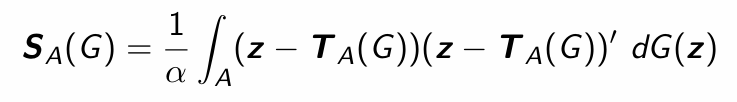
What are the functionals of the MCD estimator of location and scatter?

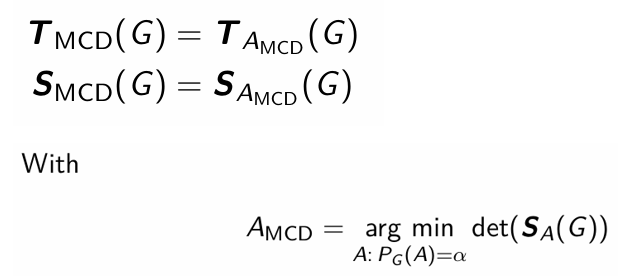
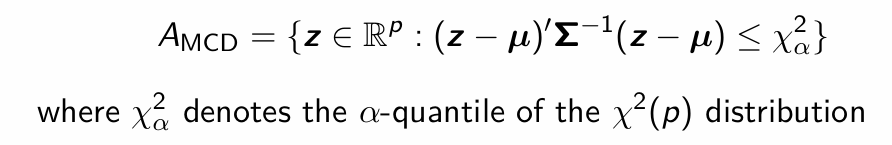
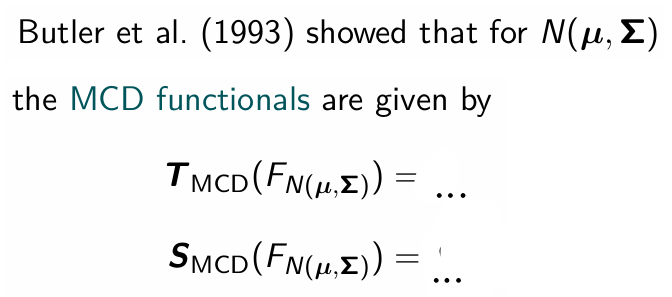
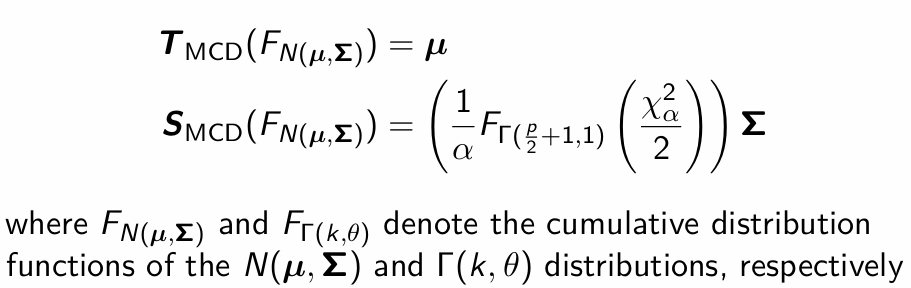
Are the MCD estimator or location and scatter Fisher consistent under a normal distribution N(µ,Σ)?

What is the Fisher consistent, robust estimator or the covariance matrix then?

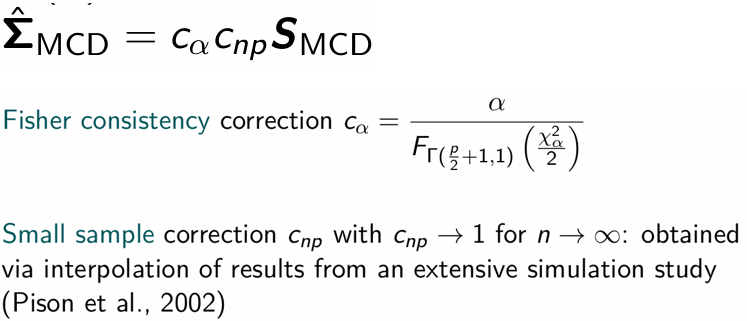
The subset size h can be seen as a conservative initial guess of the number of good data points. What is the problem with this?

Conservative choice of h trades in efficiency to ensure robustness. How can we regain some efficiency?

We use MCD estimate to detect outliers and exclude only those from estimation of mean and covariance matrix

What is Mahalanobis distance? Give the formula and explain what it means geometrically.

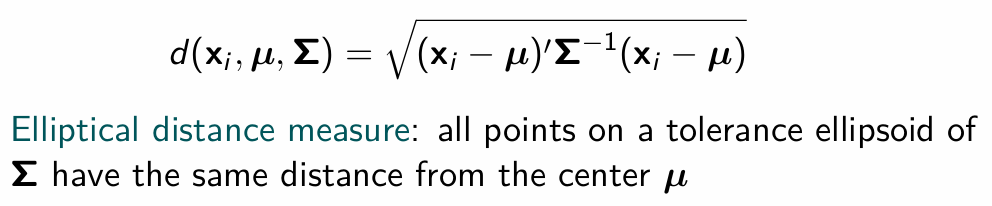
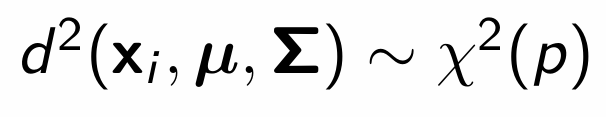
What are the weights from outlier detection via the MCD estimator?

How do we compute the reweighted MCD location estimate, given the weights?

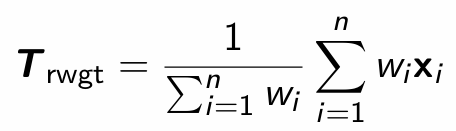
How do we compute the reweighted MCD covariance matrix estimate, given the weights?

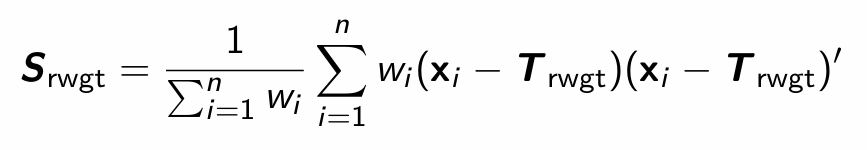
What are muhat_rwtd and sigmahat_rwtd?

When people talk about the MCD, they typically refer to …

the reweighted estimators ˆµrwgt and ˆ Σrwgt

the raw MCD estimators

What does affine equivariance imply for the data?

Data may be rotated, translated or rescaled without affecting the properties of T(X) and S(X)

When is an estimator of location T(X) affine equivariant?

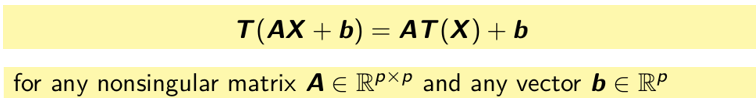
When is an estimator of scatter S(X) affine equivariant?

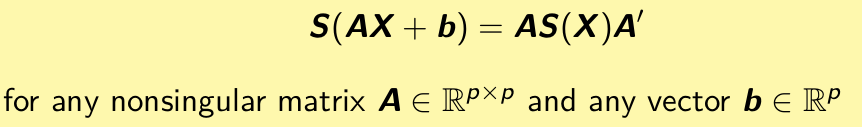
Are the reweighted MCD estimators affine equivariant? Give your reasoning.

Give the finite sample breakdown point of location estimator Tn in the multivariate setting.

Give the finite sample breakdown point of scatter estimator Sn in the multivariate setting.

What is the upper bound on the breakdown point of affine equivariant estimates of scatter?

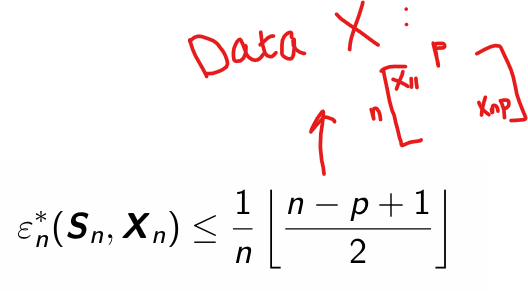
What is the upper bound on the breakdown point of affine equivariant estimates of location?

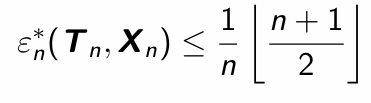
What is the optimal subset size? Maximum possible breakdown point

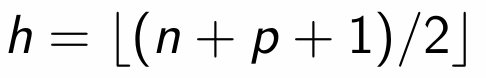
What is the distribution of the MCD estimator and its convergence rate?

asymptotically normally distributed with convergence rate √n

What is the convergence rate of the reweighted estimator?

A reweighting step does not improve the rate of convergence of the initial estimator

What is the really big problem with the MCD estimator in practice? And what is the solution?

What is the basic C-step algorithm? What is the problem with it?

If an elemental subset contains an outlier, it will influence all further iterations. In this case fully iterating C-steps until convergence is a waste of computation time.

What is the FAST-MCD Algorithm?

What is the idea of the Deterministic MCD (DetMCD) algorithm?

Instead of using many random starting values, use only a few good ones

Give the DetMCD Algorithm.

What is an alternative to MCD and all methods derived from it?

What to take away from this lecture?

If an estimator is non-parametric, does that make it robust?

No, not necessarily. The sample mean is non-parametric yet it is not robust

For a symmetric distribution, is the sample mean Fisher consistent for the true mean mu? 

Yes

For a symmetric distribution, is the sample median Fisher consistent for the true mean mu? 

Yes

For an asymmetric distribution, is the sample mean Fisher consistent for the true mean mu? 

Yes

For an asymmetric distribution, is the sample median Fisher consistent for the true mean mu? 

No (so we would need a correction)

For an asymmetric distribution, is the sample mean Fisher consistent for the median?

No (so we would need a correction)