Linear Vector Spaces Exam 1
0.0(0)
Studied by 0 people
Call Kai
Learn
Practice Test
Spaced Repetition
Match
Flashcards
Knowt PlayCard Sorting
1/8
There's no tags or description
Looks like no tags are added yet.
Last updated 5:35 AM on 9/25/25
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
9 Terms
1
New cards
Addition Properties that must be satisfied for a vector space
2
New cards
Scalar Multiplication Properties that must be satisfied for a vector space,
3
New cards
Subspaces: M subset of V is a subspace if
4
New cards
Norms: A norm ||.|| on vector space V satisfies:
5
New cards
Inner Products: An inner product <.,.> on V satisfies:
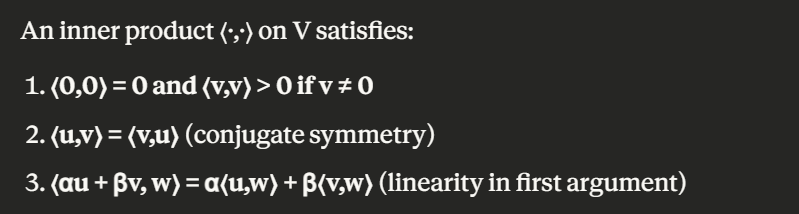
6
New cards
Linear Independence/Dependence: Set S = {v_1, …, v_n} is
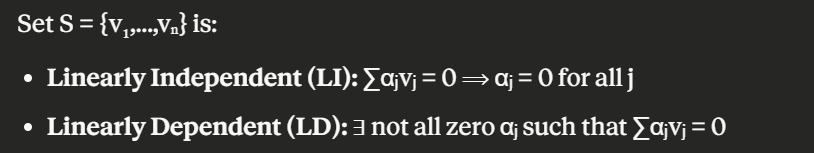
7
New cards
Span {v_1, …, v_n} is always a
Subspace
8
New cards
S is Linearly Dependent iff
at least one vector is a linear combination of the others
9
New cards
Rank-Nullity Theorem
dim(V) = dim(Ker(T)) + dim(R(T))
Note 
Flashcards (45)