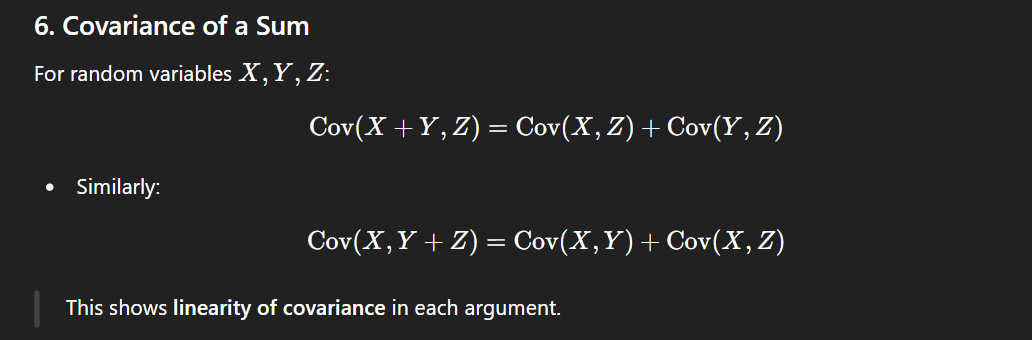Expected value and variance rules ML1

What is the expected value of a discrete X? so E[X] when discrete

See image

What is the expected value of a continuous X? so E[X] when continuous

See image, and it would be the PDF over the max and min range of the function.

split up E[aX + bY]

where a and b are constants

a*E[X] + b*E[Y]

so keep in mind

E[X + Y] = E[X] + E[Y]

and 

E[X*5] = 5 * E[X]

Can you take a sum out of the expected value?

Yes you can.

Can you always perform

E[X*Y] = E[X] * E[Y]

No you can not, this has to be when X and Y are independent from each other.

How to express E[X] in form of E[X|Y]

E[X] = E[E[X|Y]]

Write the variance in terms of Expectation

So VAR[X] = …

using only E[X]

VAR[X]  = E[(X-E[X])²]= E[X²] - (E[X])²

The proof is in the image.

What is VAR[c] where c is a constant

VAR[c] = 0

Rewrite VAR[aX] where a is a constant

a² * VAR[x]

pay attention, that the constant is now squared

Rewrite VAR[X+b] where b is a constant

VAR[X+b] = VAR[X]

Adding a constant shifts the distribution but does not change the spread.

Rewrite Var[X+Y]

Var[X+Y] = Var[X] + Var[Y] + 2Cov[X,Y]

Write Cov[X,Y] in terms of E[X] and E[Y]

Cov[X,Y] = E[(X−E[X])(Y−E[Y])] = E[XY]−E[X]E[Y]

• Positive covariance → Xand Y tend to increase together.

• Negative covariance → one tends to increase while the other decreases.

What is COV[X,X]

Cov[X,X] = Var[X]

Is covariance symmetric?

Yes, Cov[X,Y] = Cov[Y,X]

Rewrite Cov[aX,bY]

where a and b are constants

a*b*cov[X,Y]

Rewrite

Cov(X+Y,Z)

and

Cov(X,Y+Z)

Cov(X+Y,Z)=Cov(X,Z)+Cov(Y,Z)

and

Cov(X,Y+Z)=Cov(X,Y)+Cov(X,Z)