gcse maths + further maths formulas

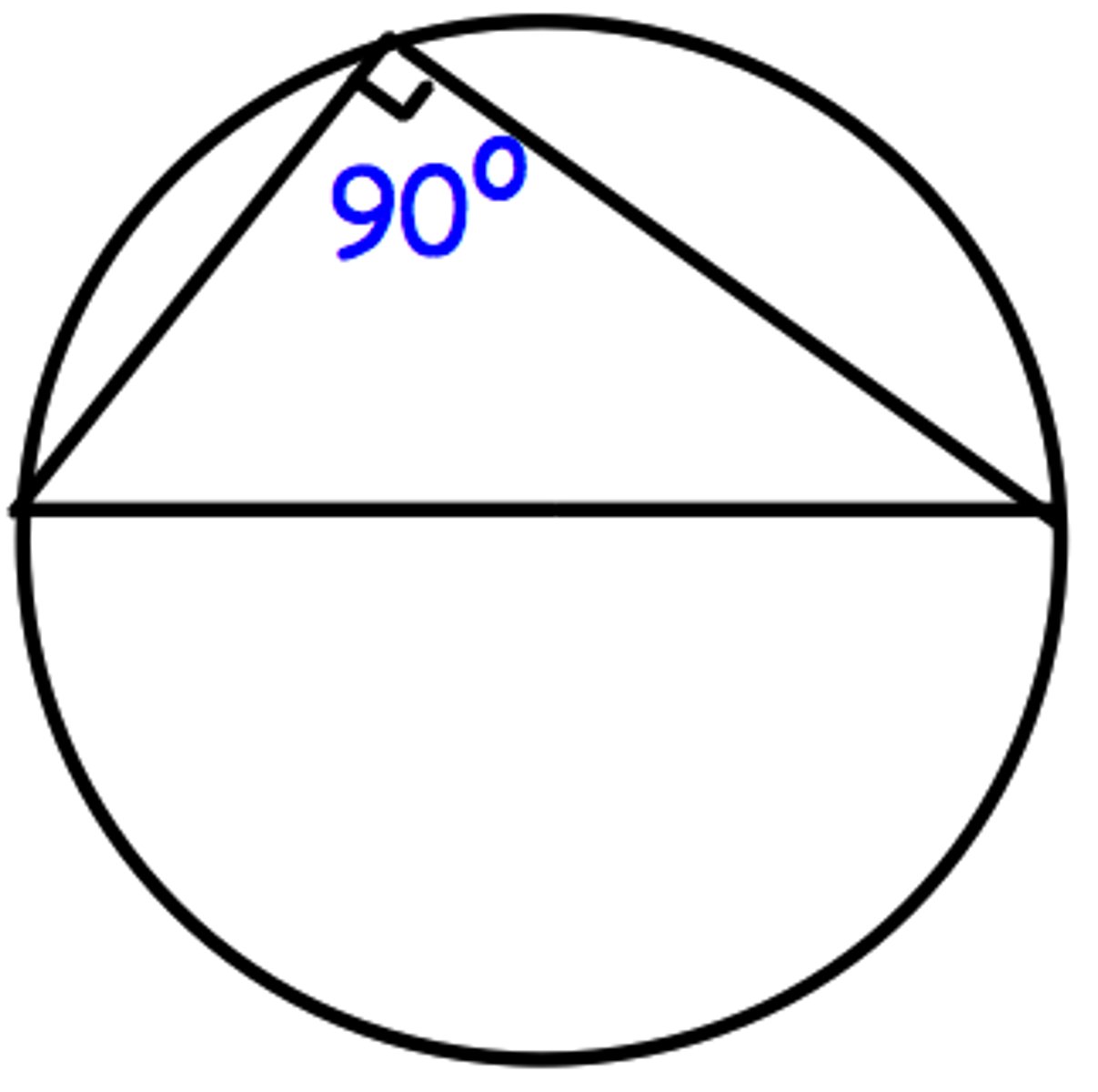
the angle in a semicircle is 90'

state the appropriate circle theorem

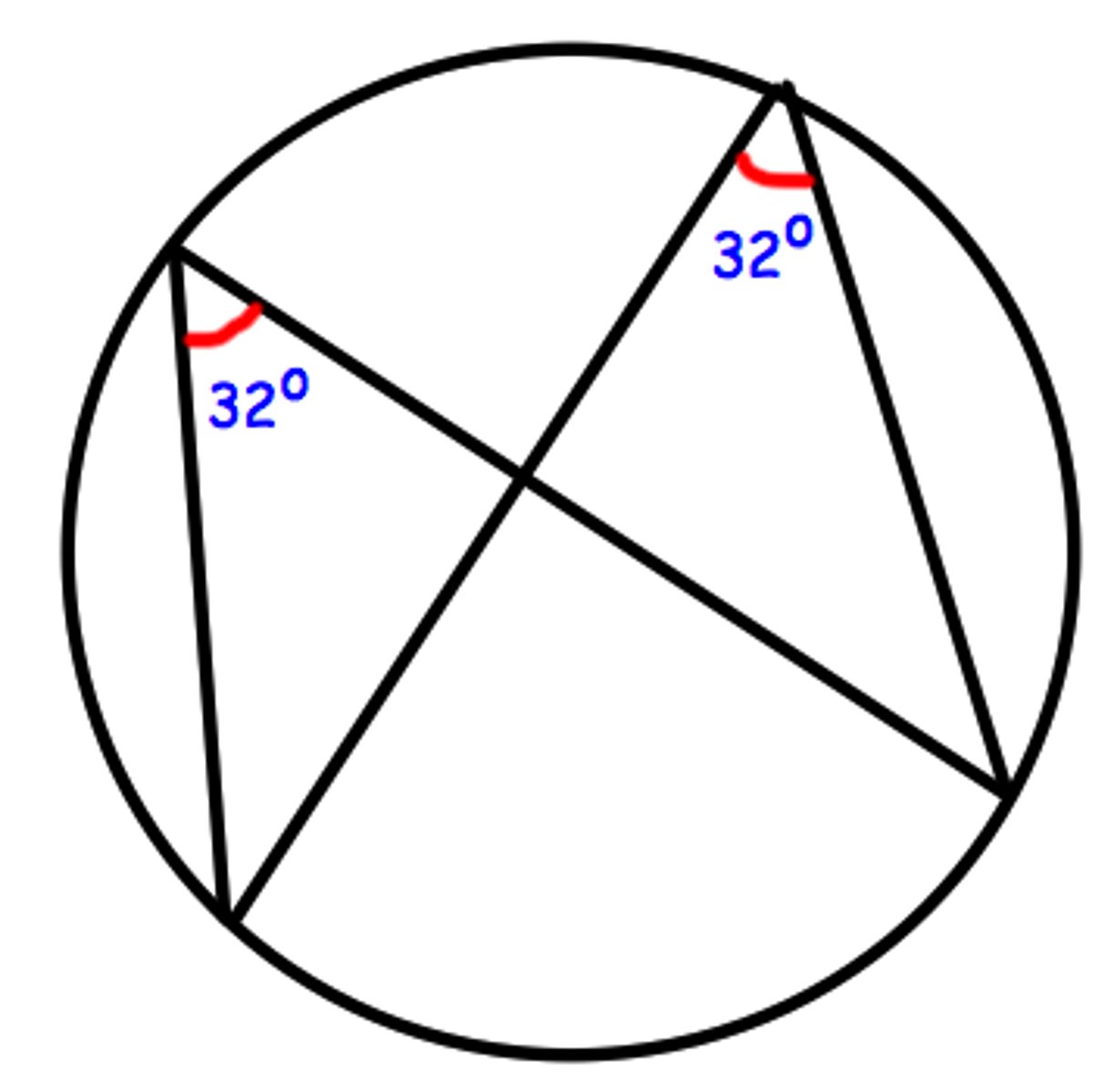
the angle at the circumference is half the angle at the center

state the appropriate circle theorem

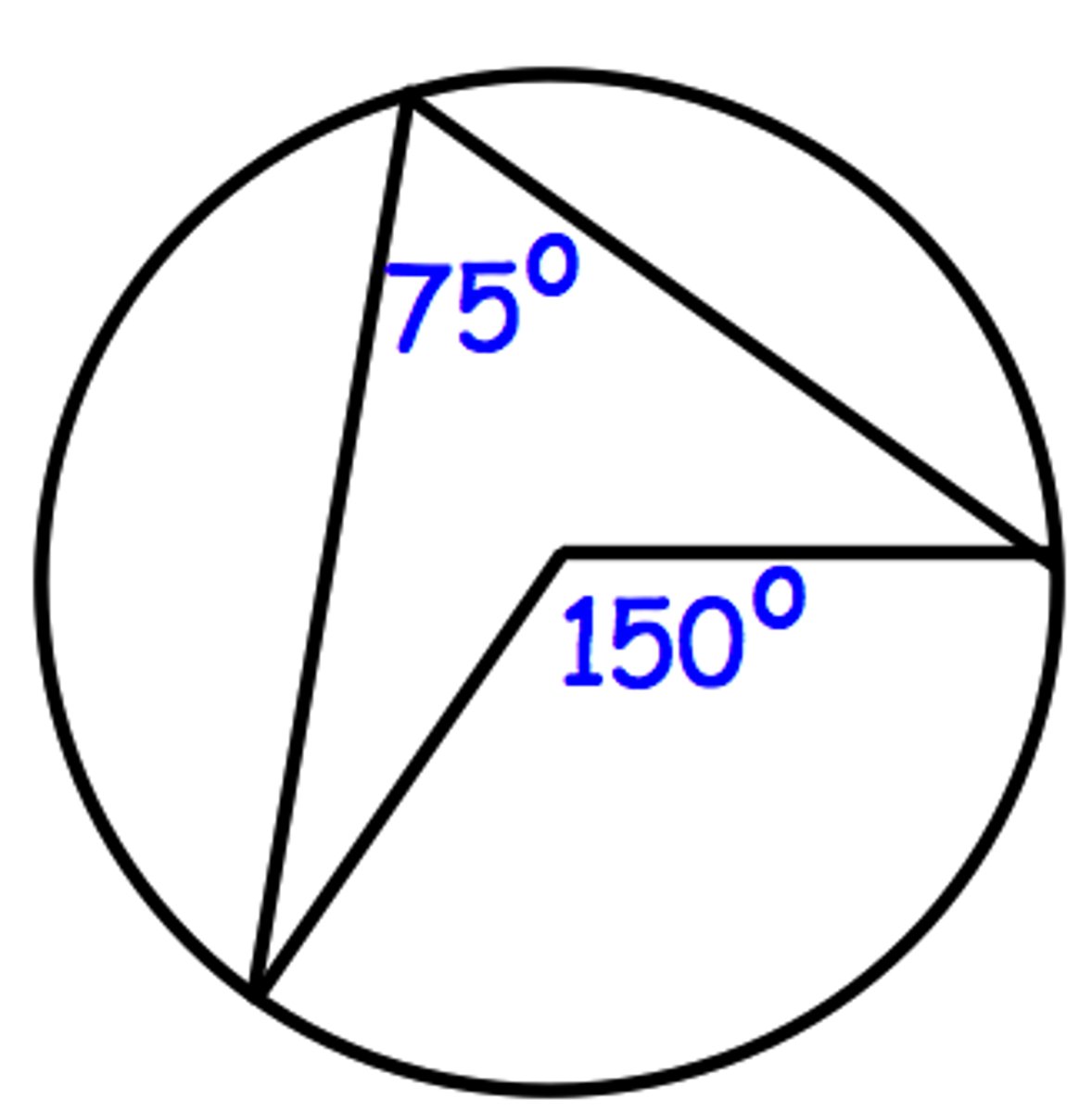
Angles in the same segment of a circle are equal

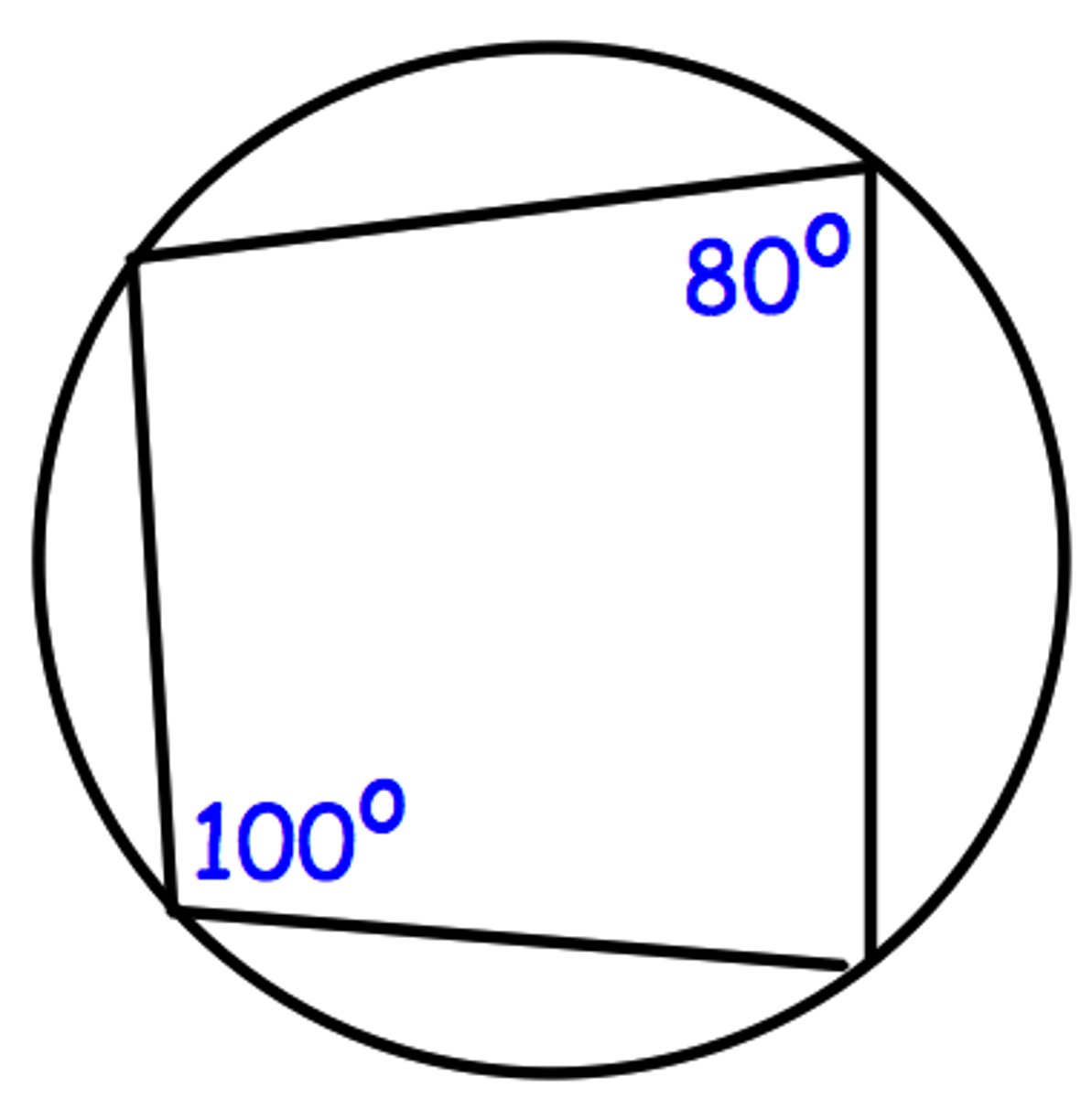
state the appropriate circle theorem

opposite angles in a cyclic quadrilateral add to 180

state the appropriate circle theorem

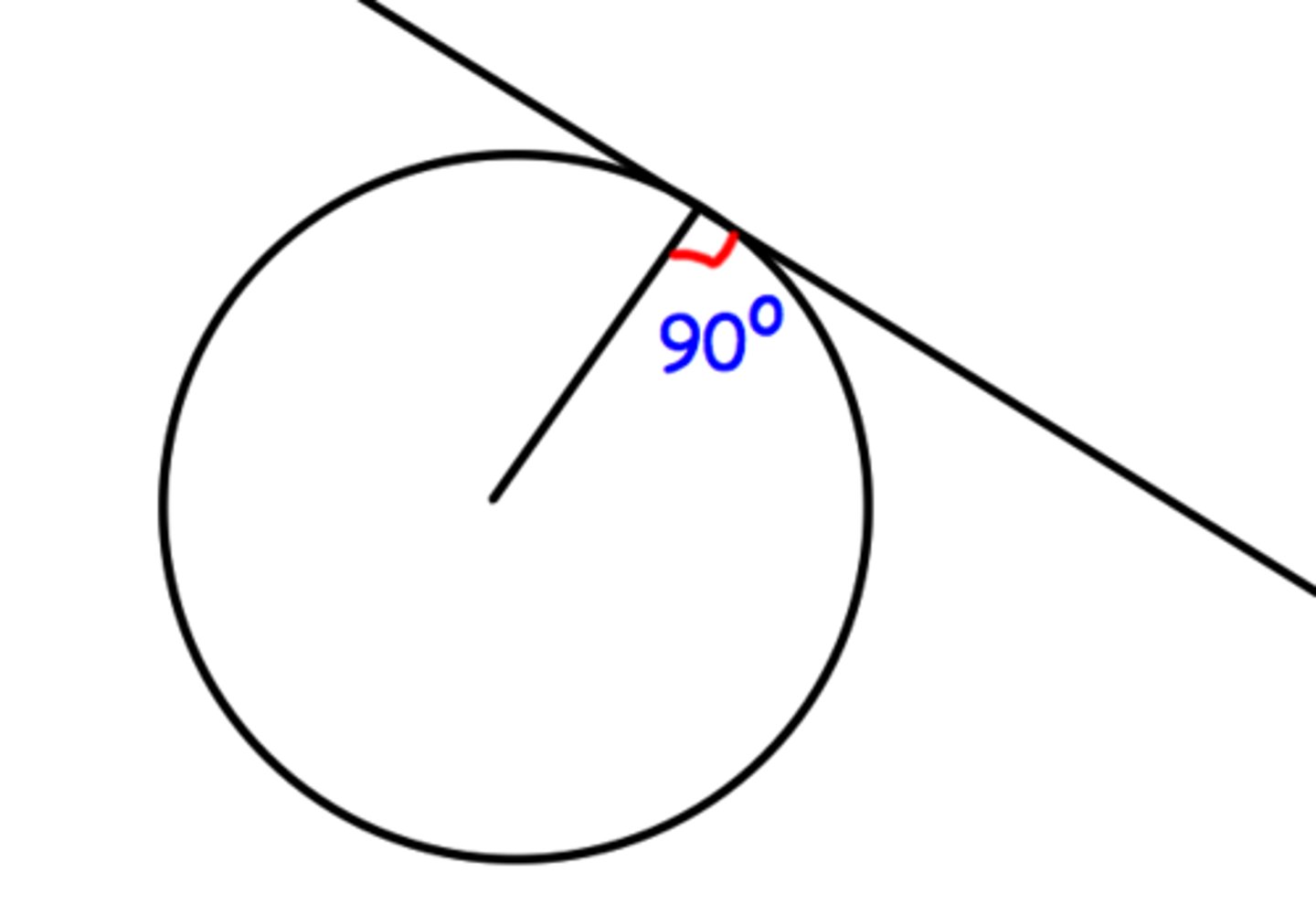
the angle between a radius and a tangent is always 90'

state the appropriate circle theorem

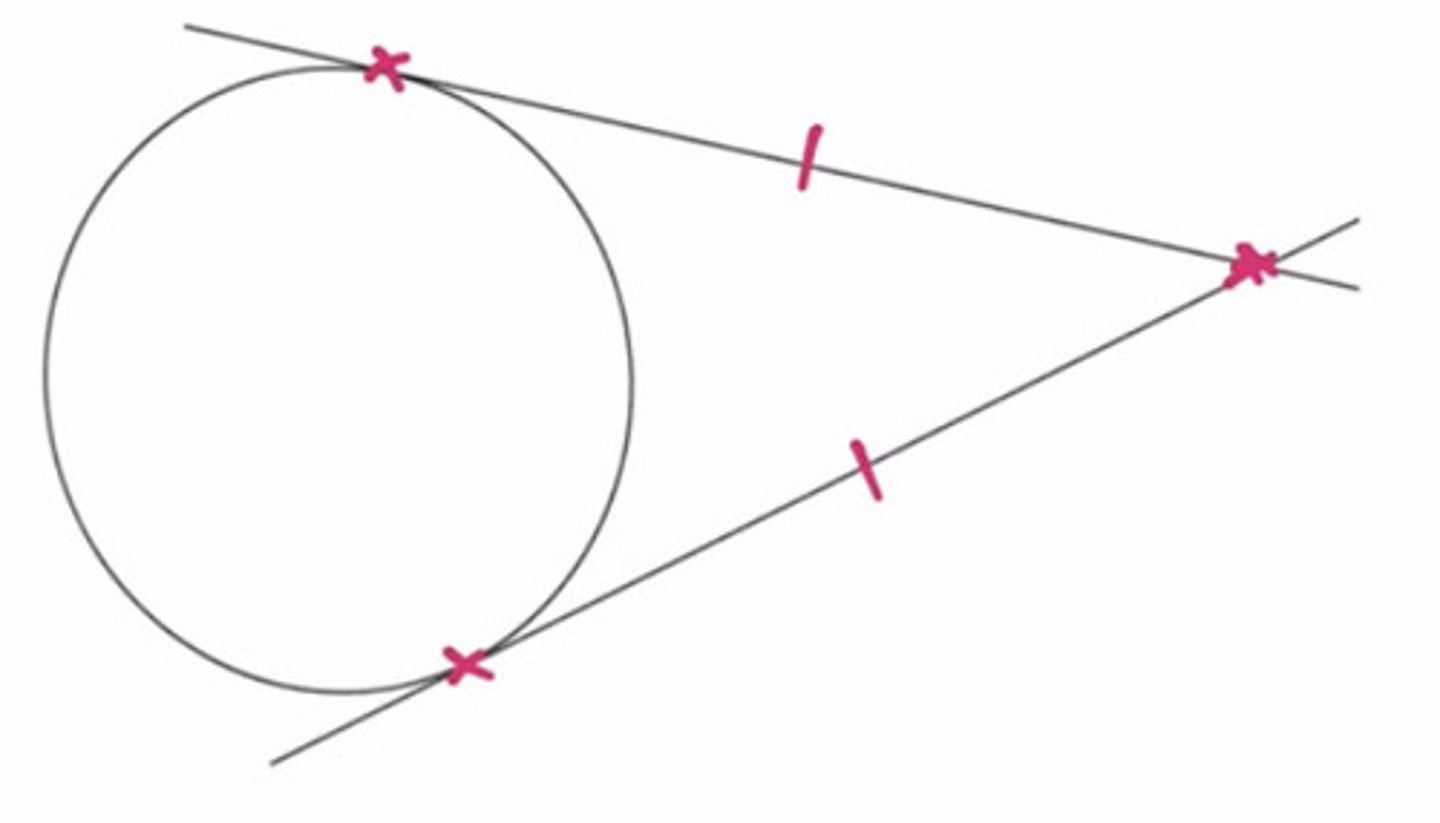
Two tangents meet at equal length

state the appropriate circle theorem

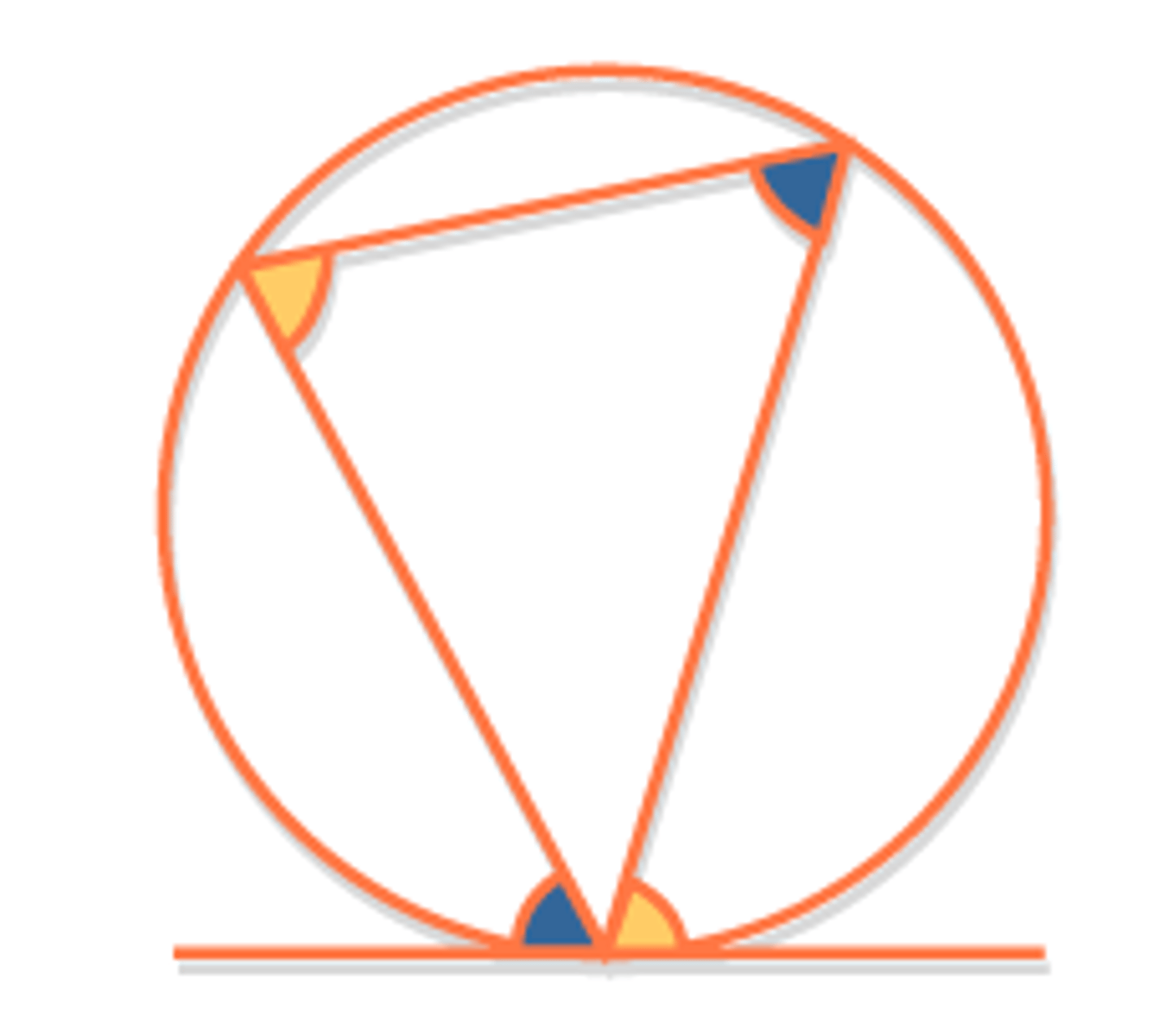
Alternate segment theorem

state the appropriate circle theorem

vertical translation by a units

f(x) --> f(x)+a

horizontal translation by -b units

f(x) --> f(x+b)

vertical stretch scale factor c

f(x) --> cf(x)

horizontal stretch scale factor 1/K

f(x) --> f(Kx)

unfactorised quadratic y intercept

how to find y intercept

factorised quadratic x's so that each bracket equals 0

how to find the x intercepts

complete the square x so the bracket = 0 and y the bit outside the bracket

how to find the minimum point

dy/dx=...+ nk xⁿ⁻¹+...

y=... +k xⁿ+...

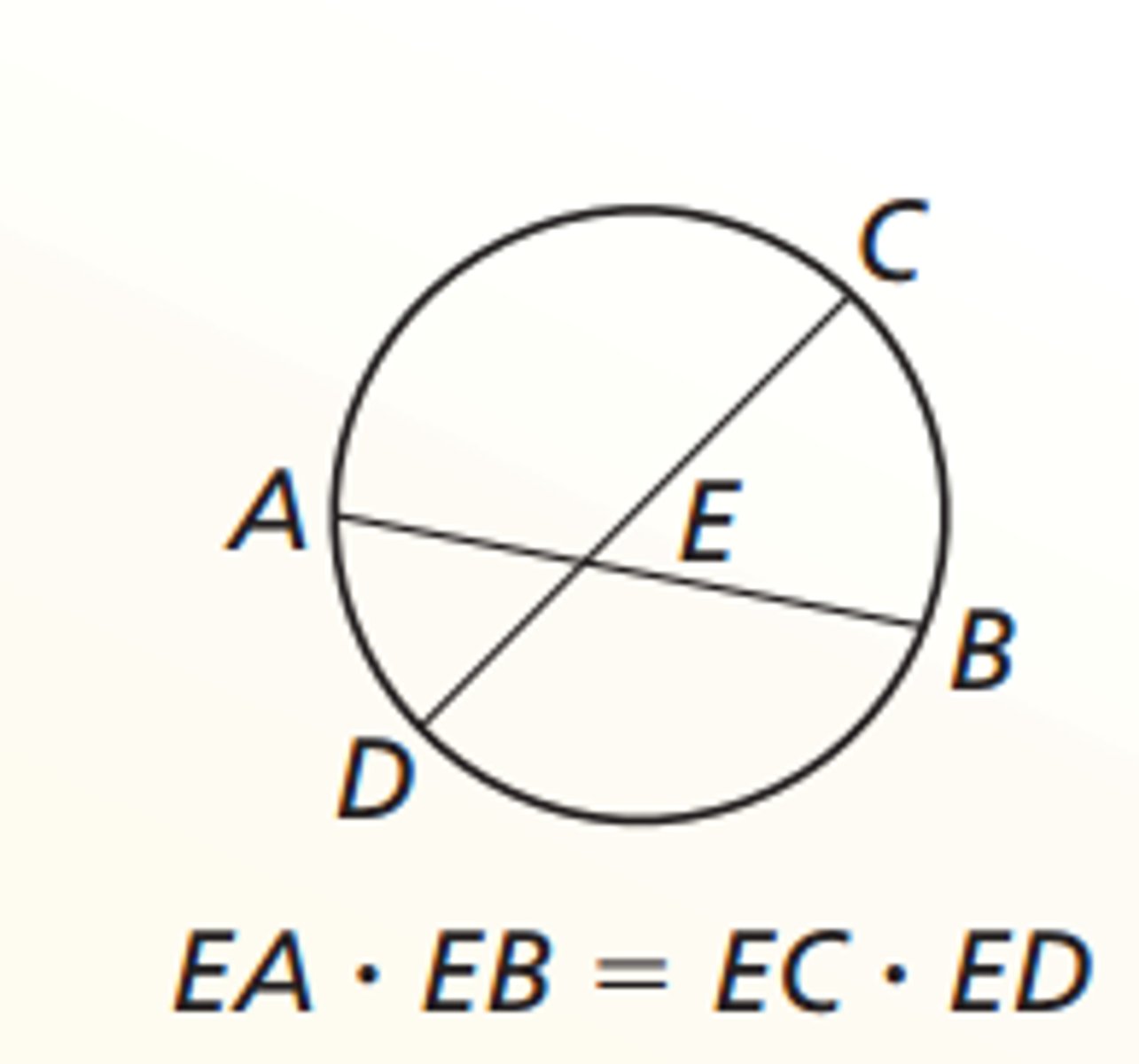
AX x BX = CX x DX

intersecting chords

Area of any triangle

1/2absinC

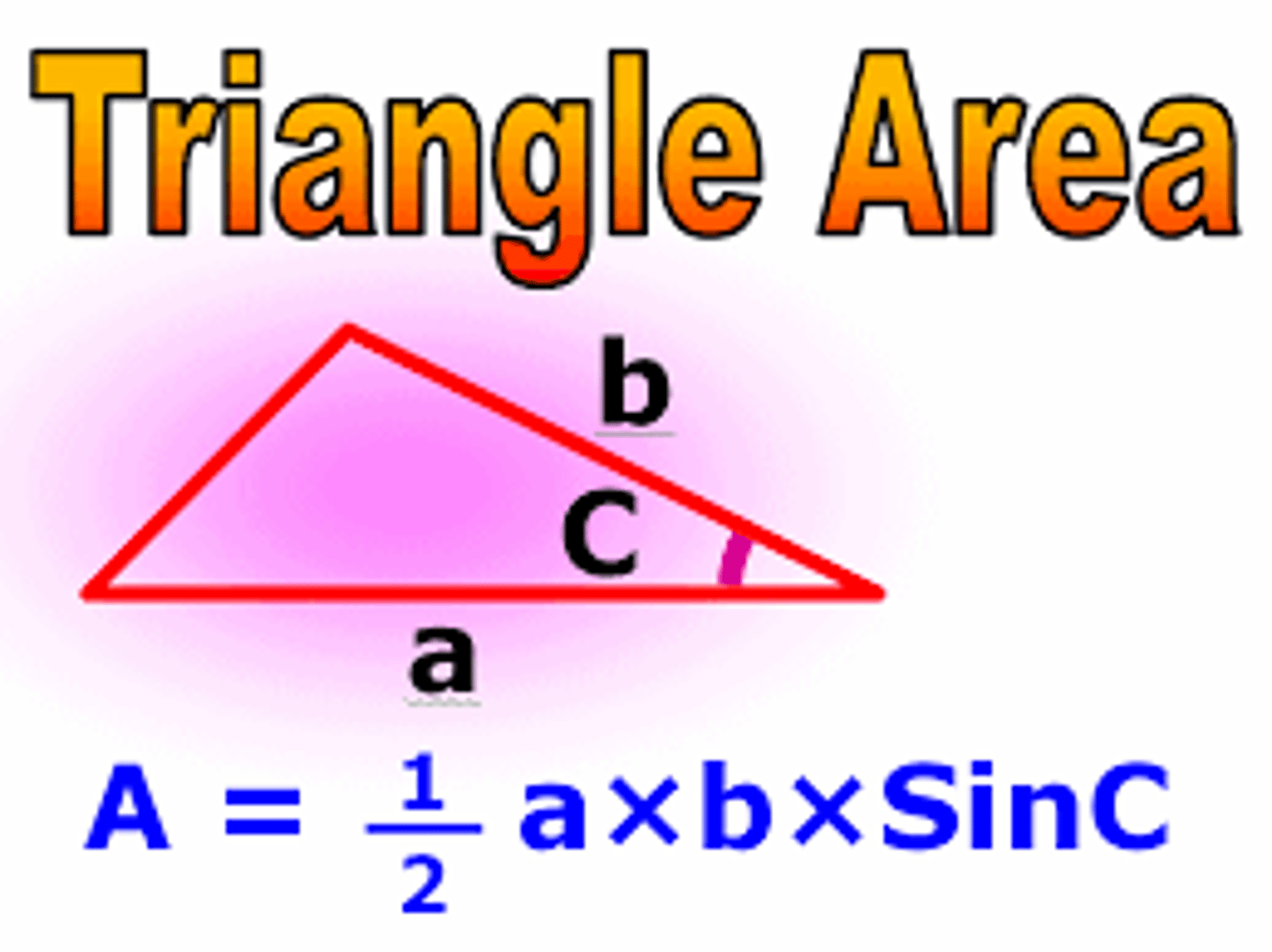
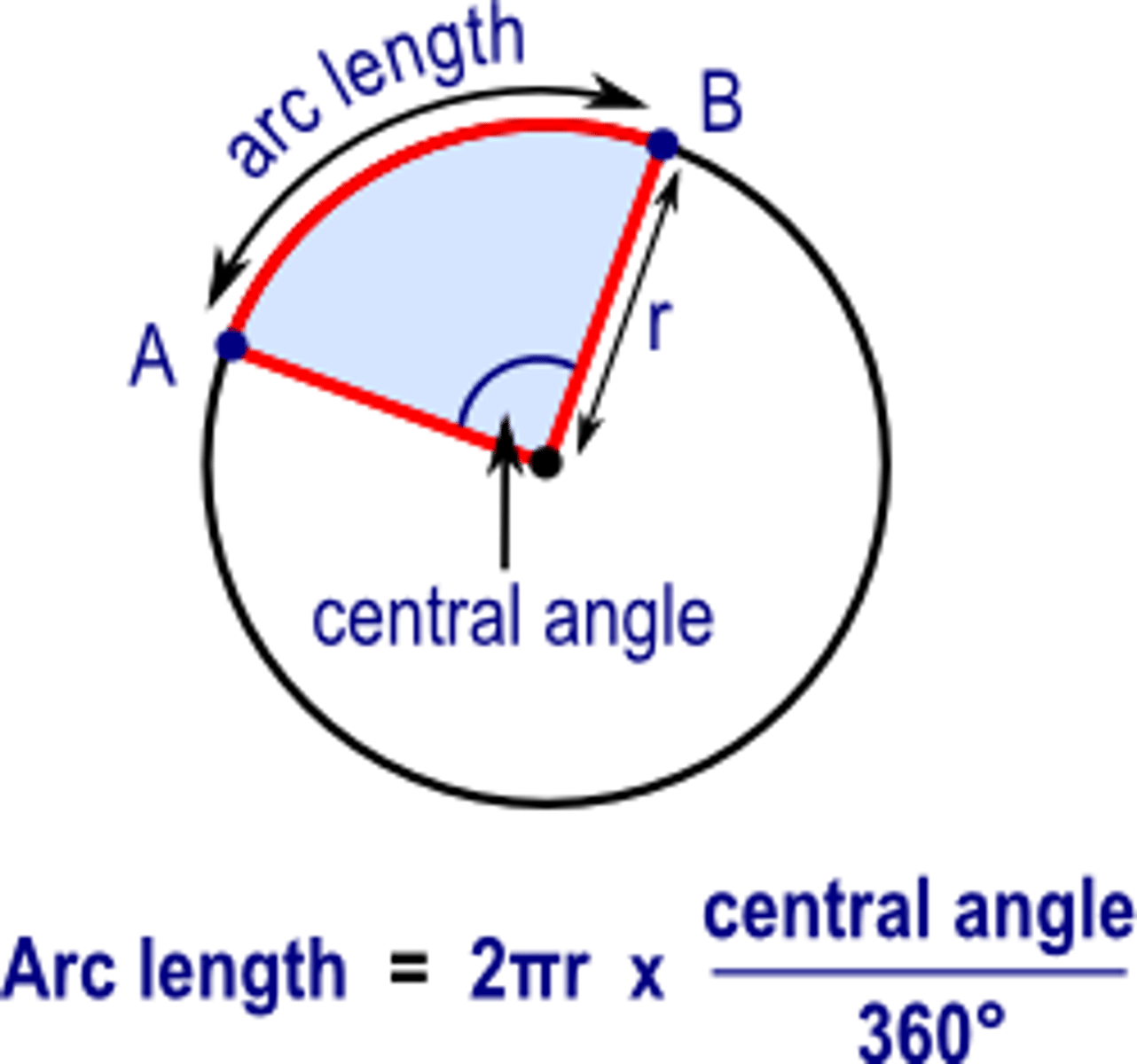
length of an arc

Length of an Arc = (central angle/360) x 2πr

Perimeter of a sector

Arc length + 2r

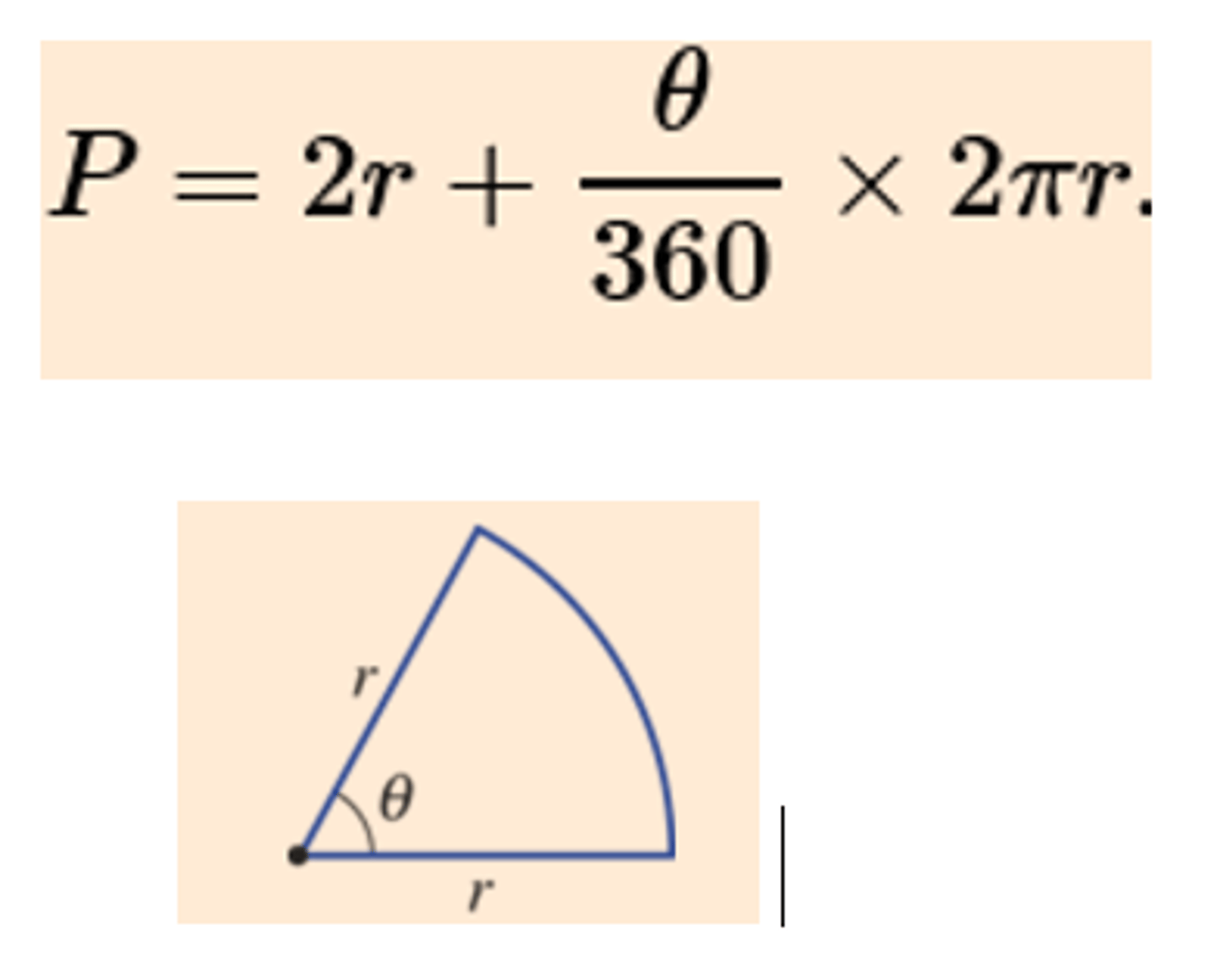
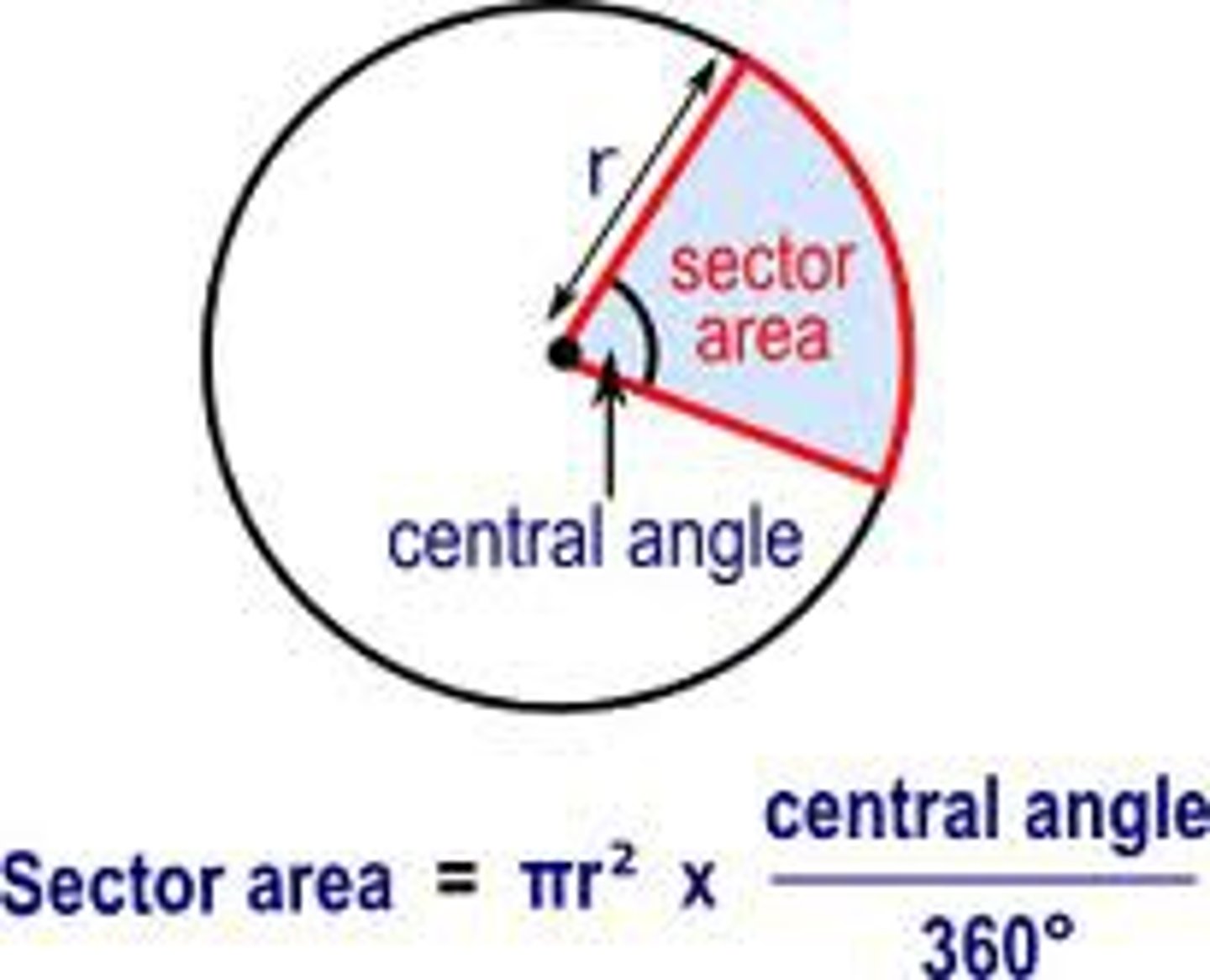
Area of a sector

Area of a Sector = (central angle/360) x πr²

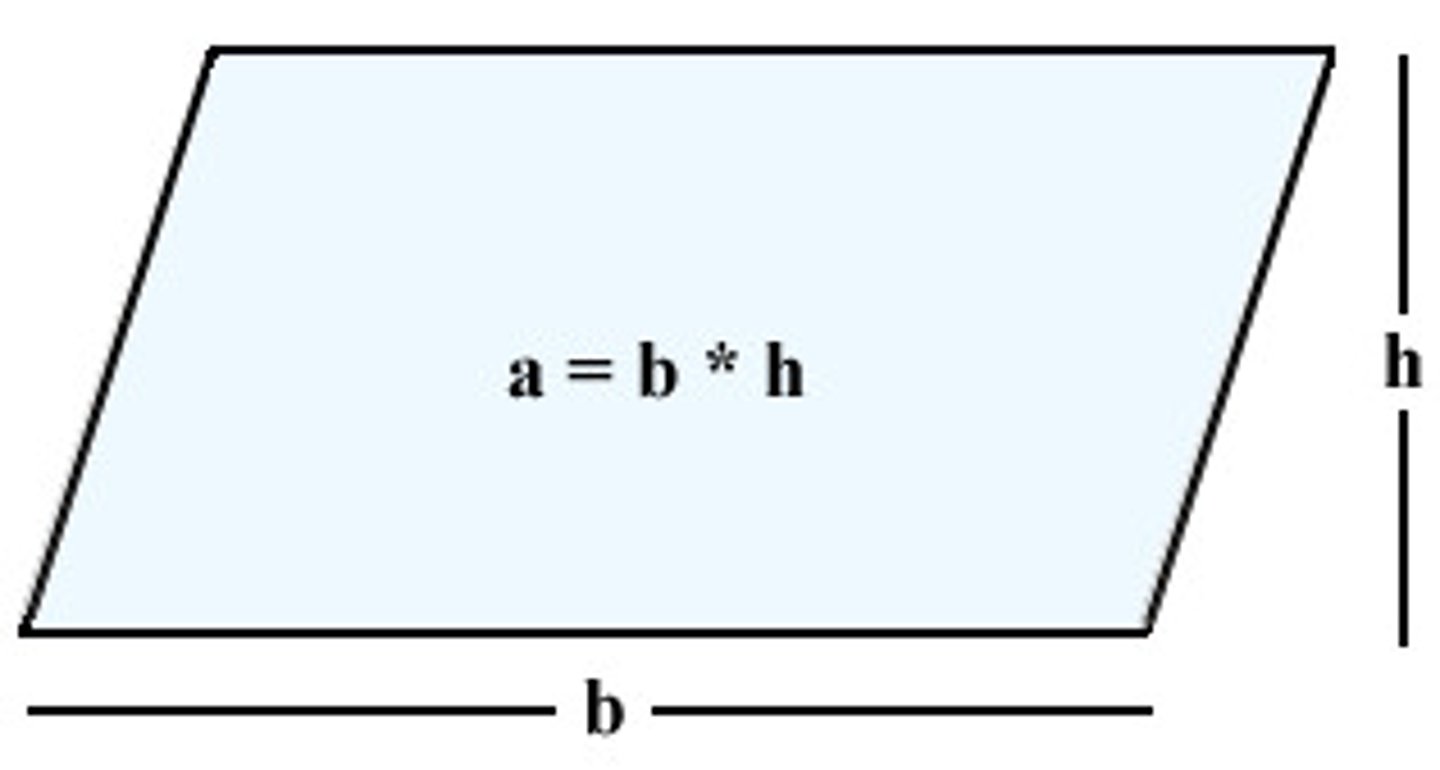
Area of a parallelogram formula

A=bh

Area of trapezium formula

1/2(a+b)h

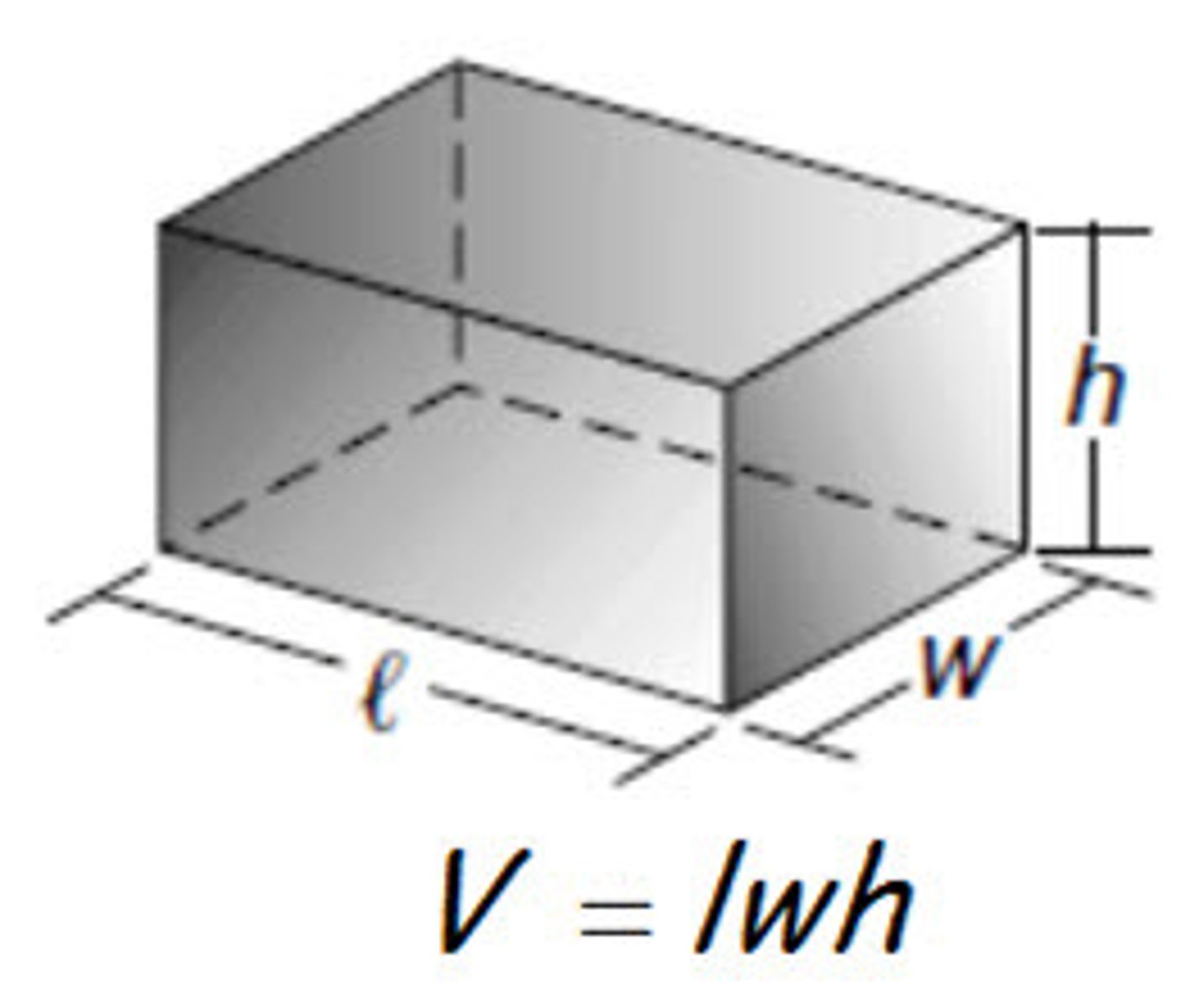
volume of a prism

Area of cross section x length

Volume of a cylinder

V=πr²h

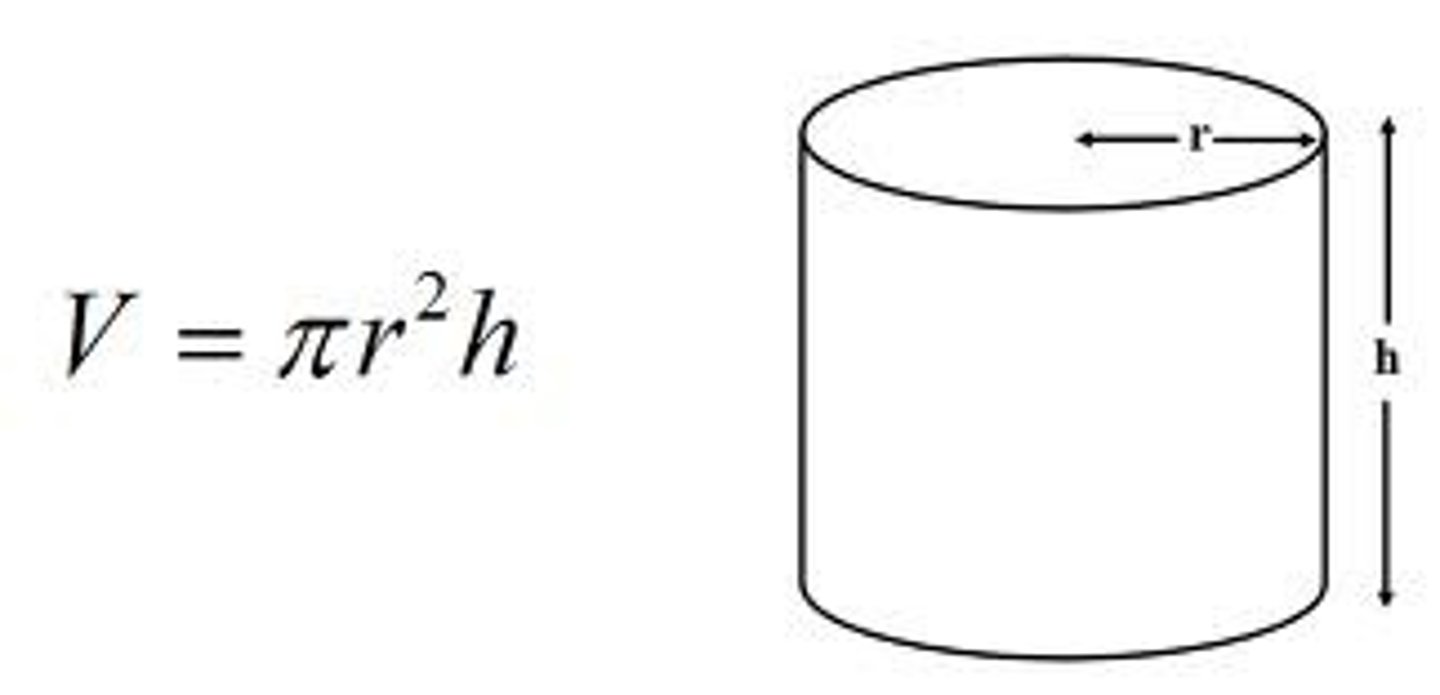
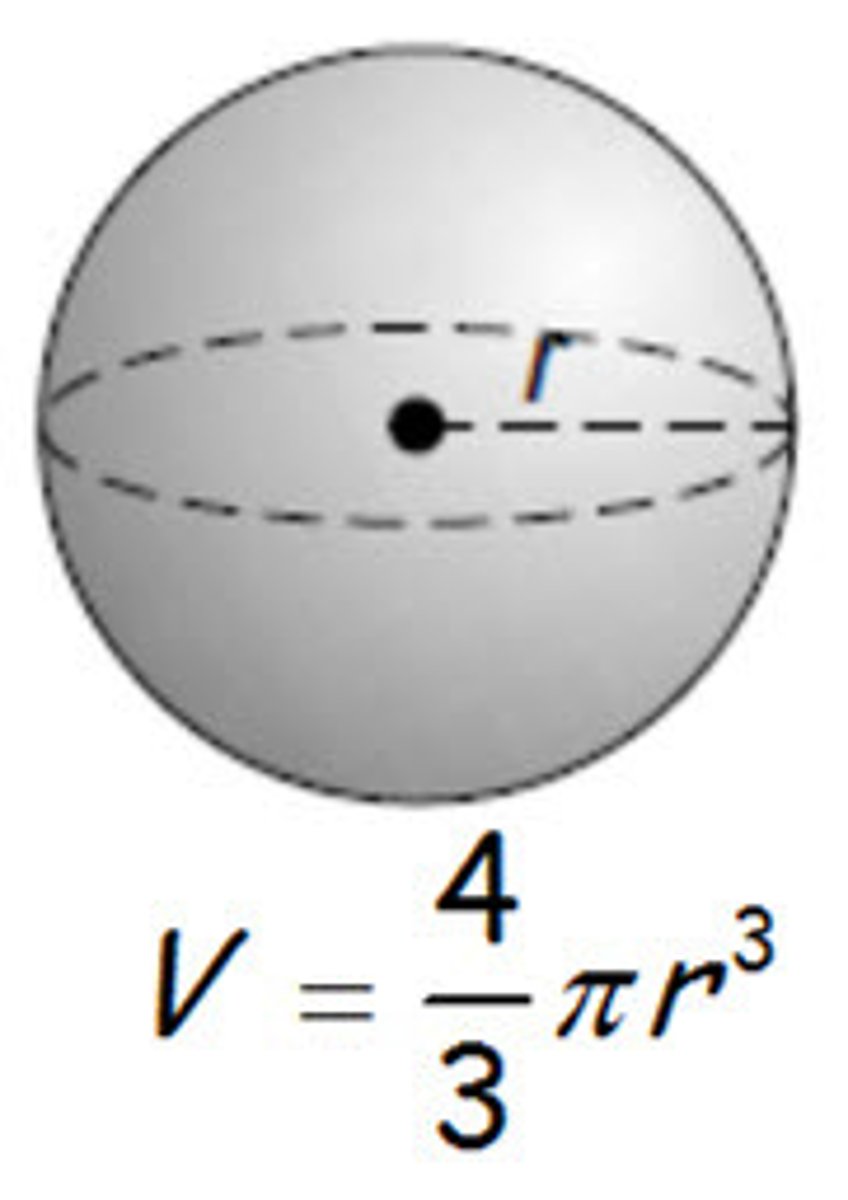
Volume of a sphere

4/3πr³

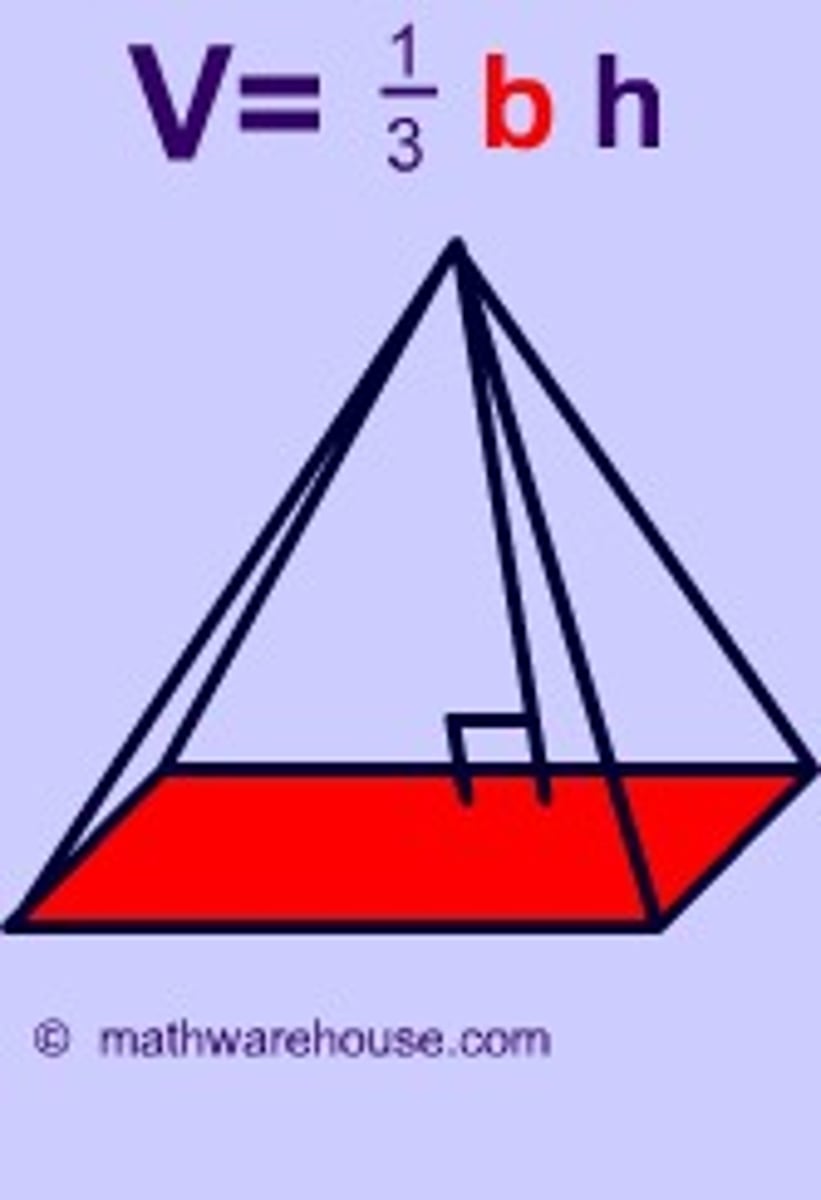
volume of a pyramid

1/3 x area of base x height

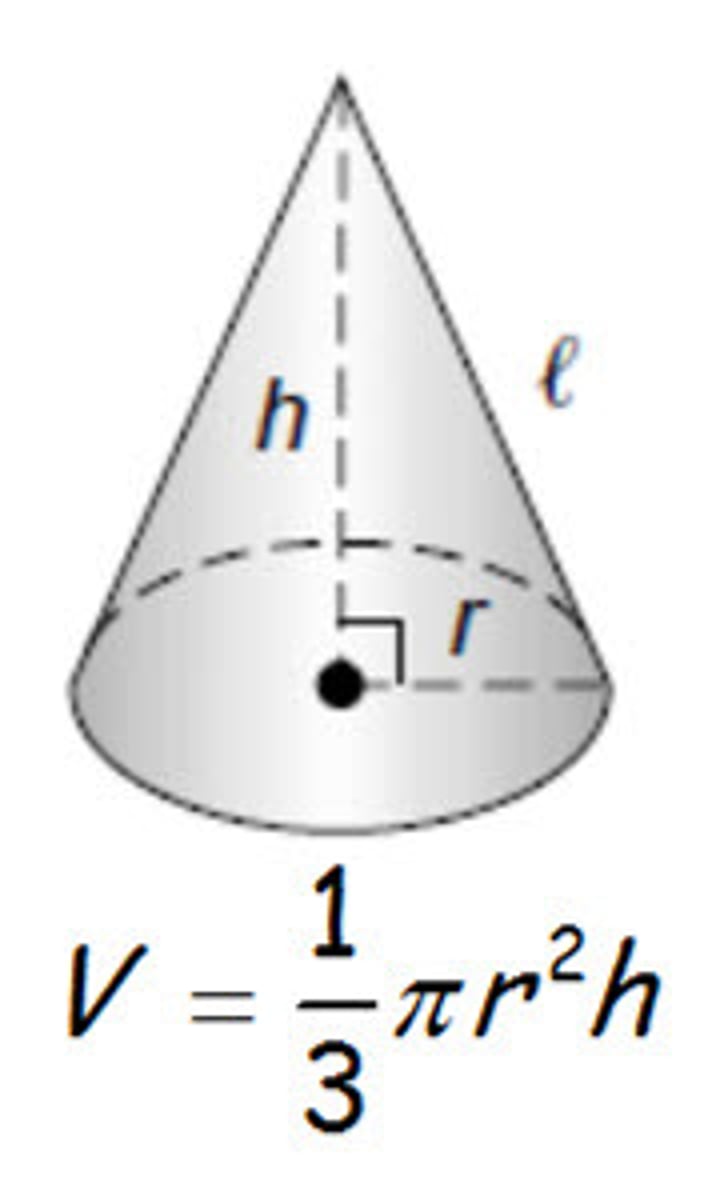
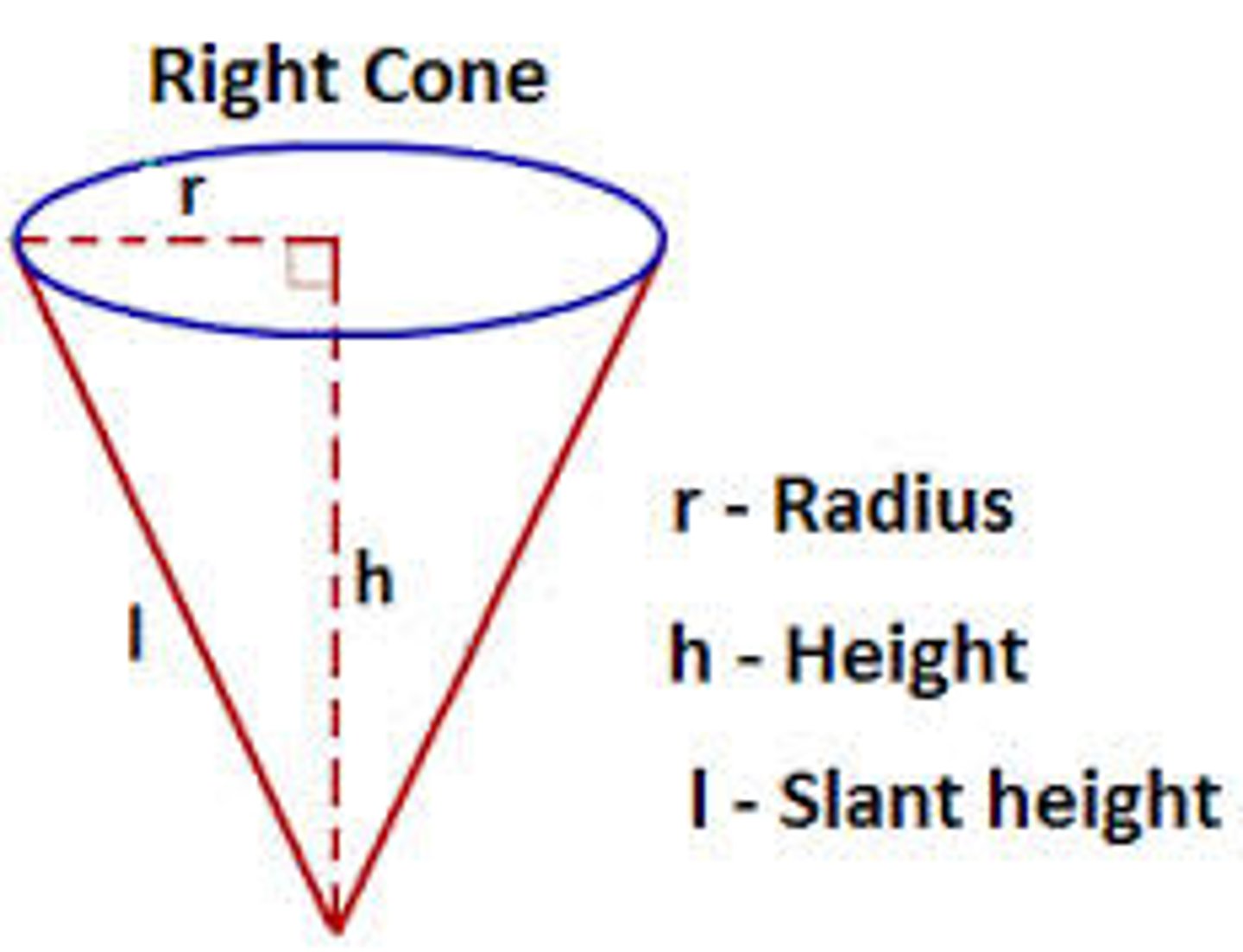
Volume of a cone

1/3πr²h

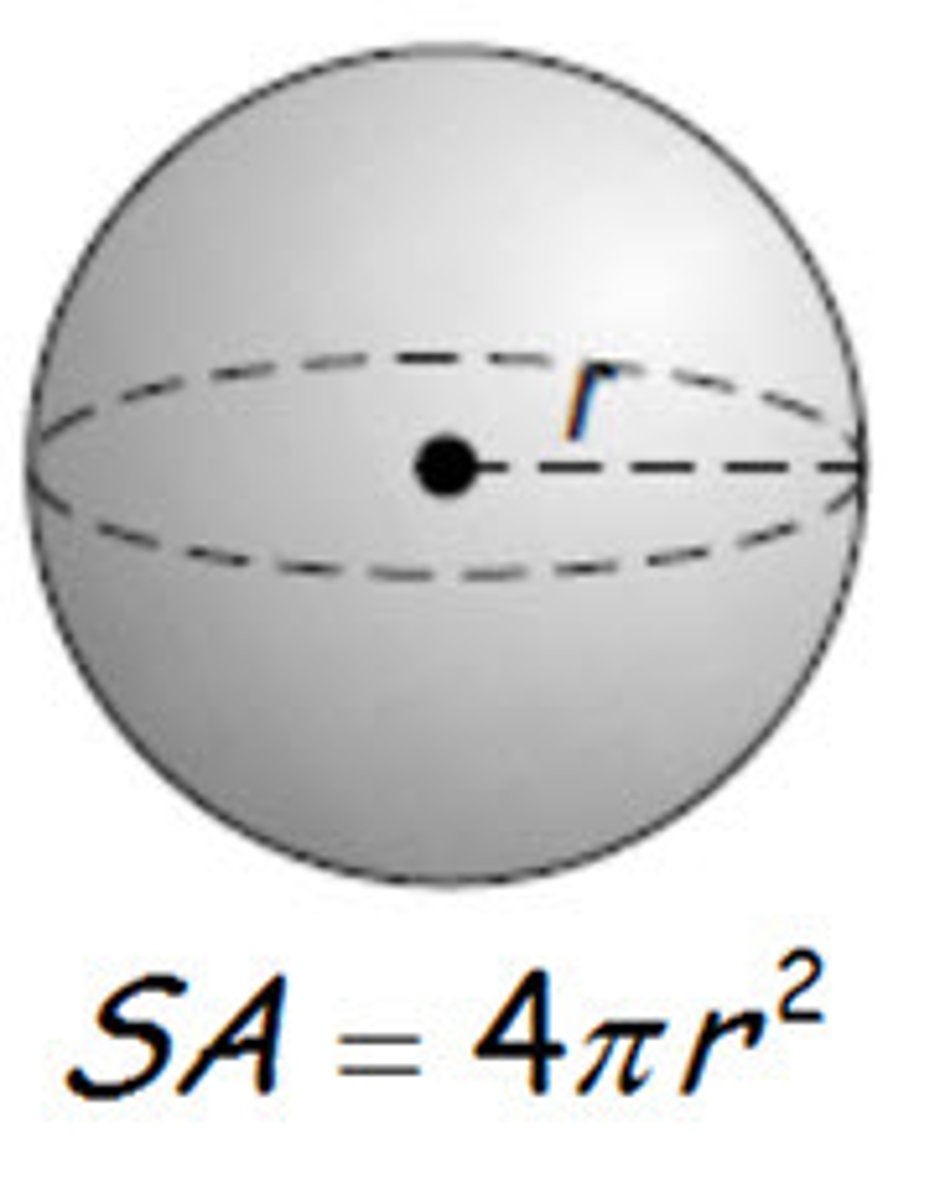
Surface area of a sphere

4πr²

Surface Area of a Cylinder

2πrh+2πr²

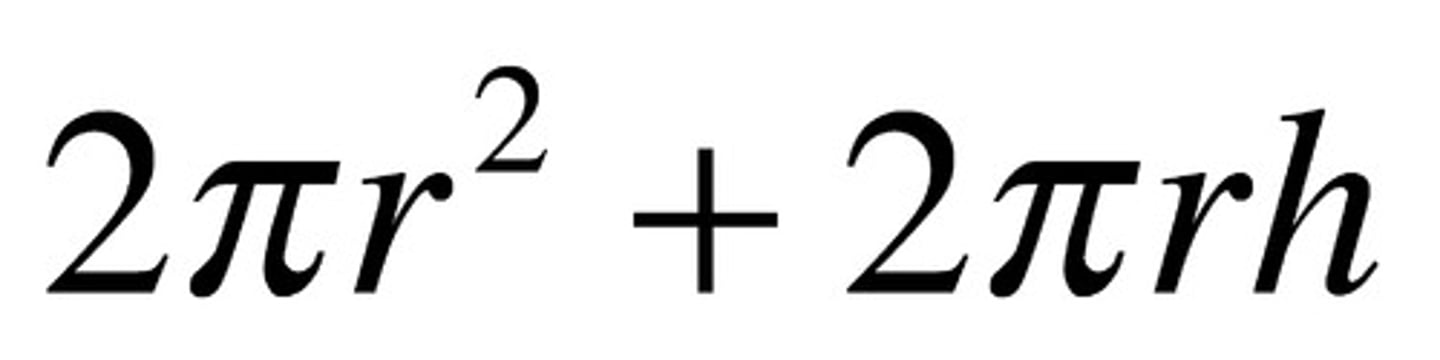
Surface Area of a Cone

πrl+πr²

Invarient

In mathematics, an invariant is a property, held by a class of mathematical objects, which remains unchanged when transformations of a certain type are applied to the objects.

Quadratic Formula

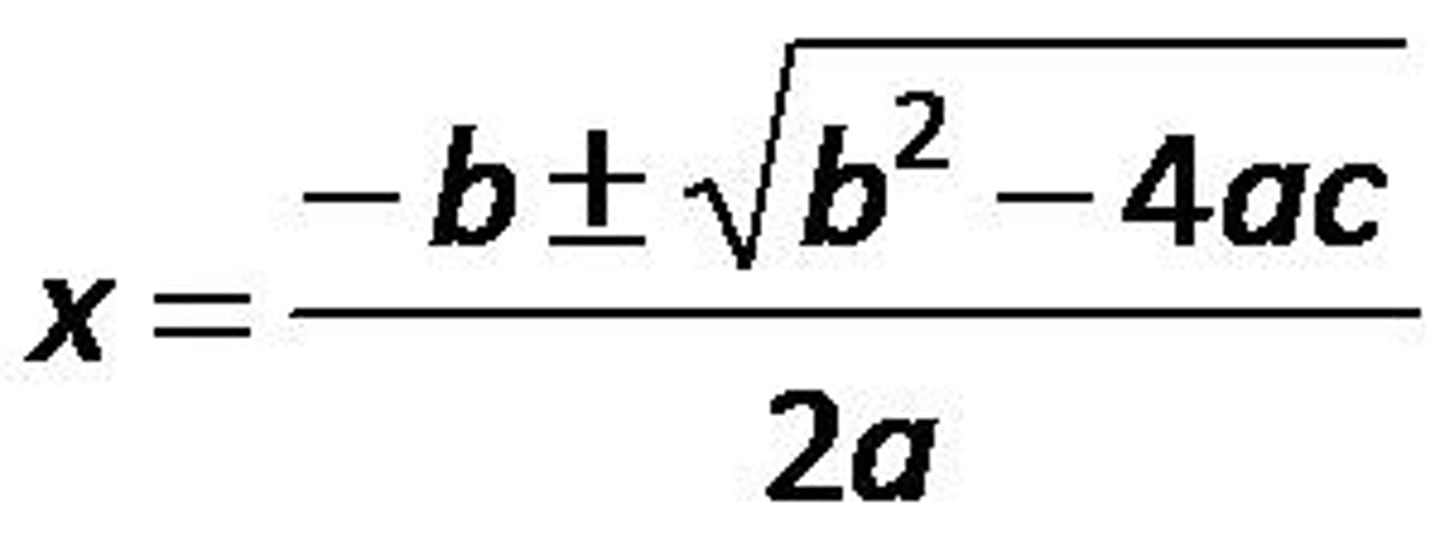
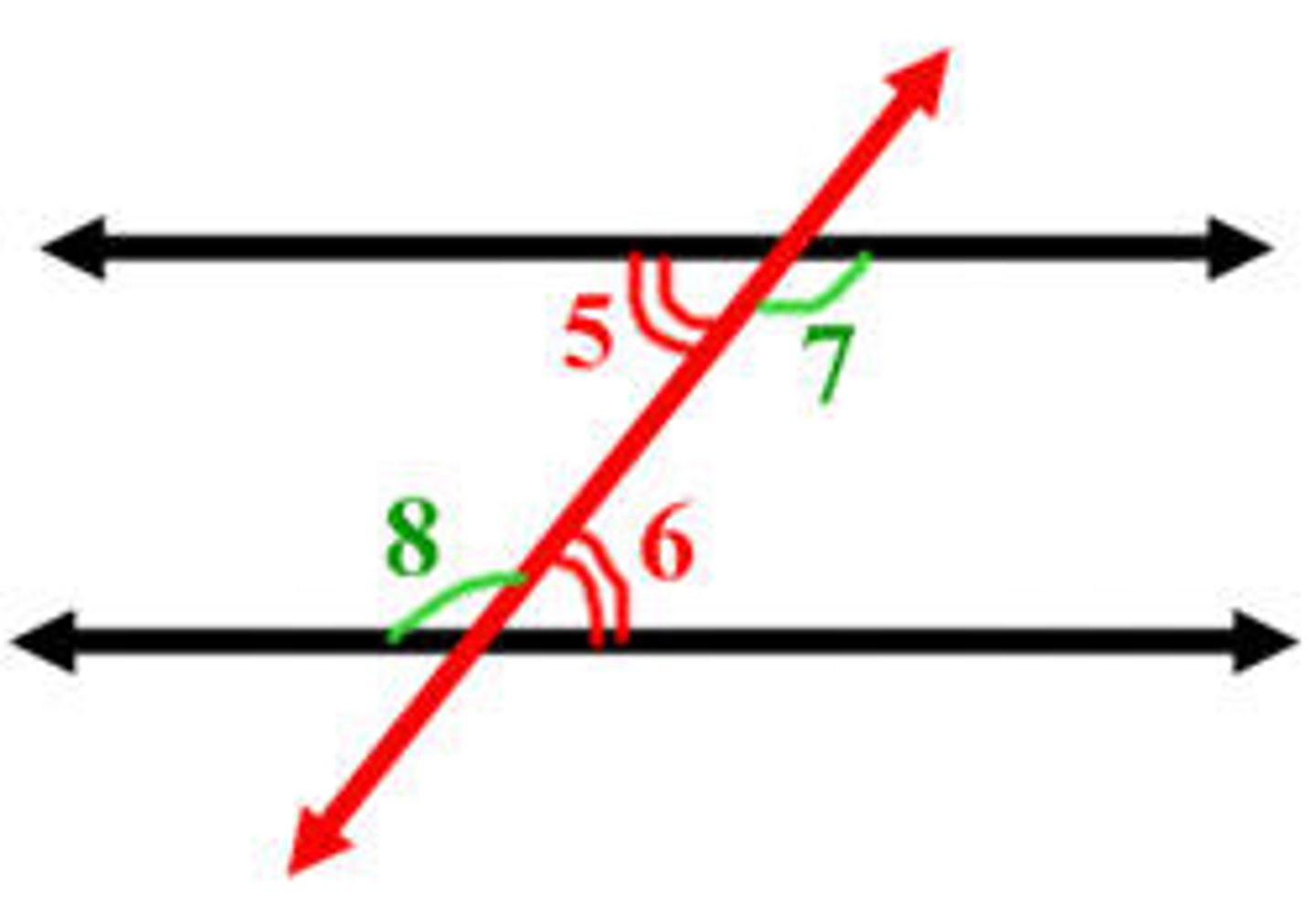
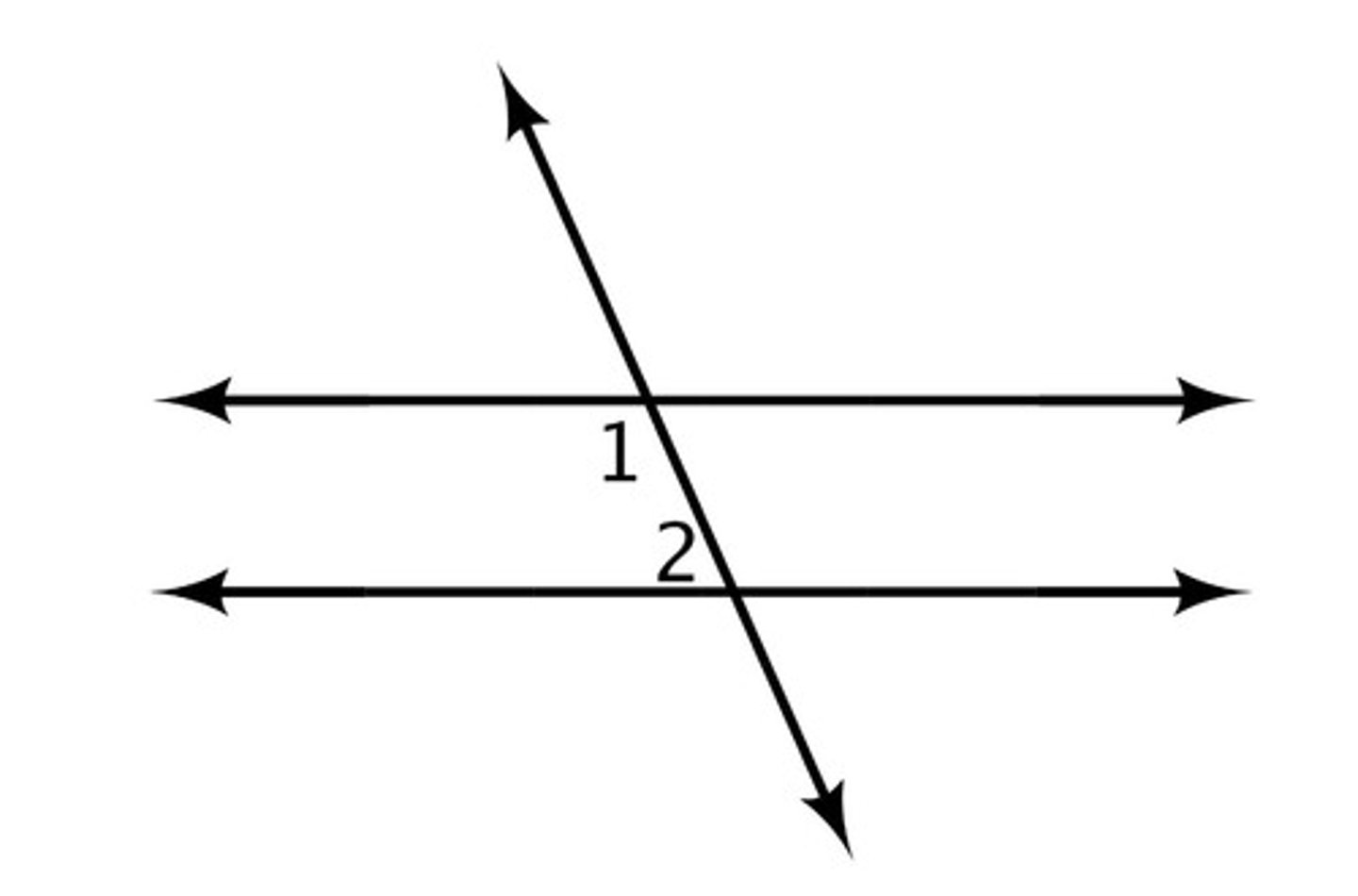
corresponding angles

alternate angles

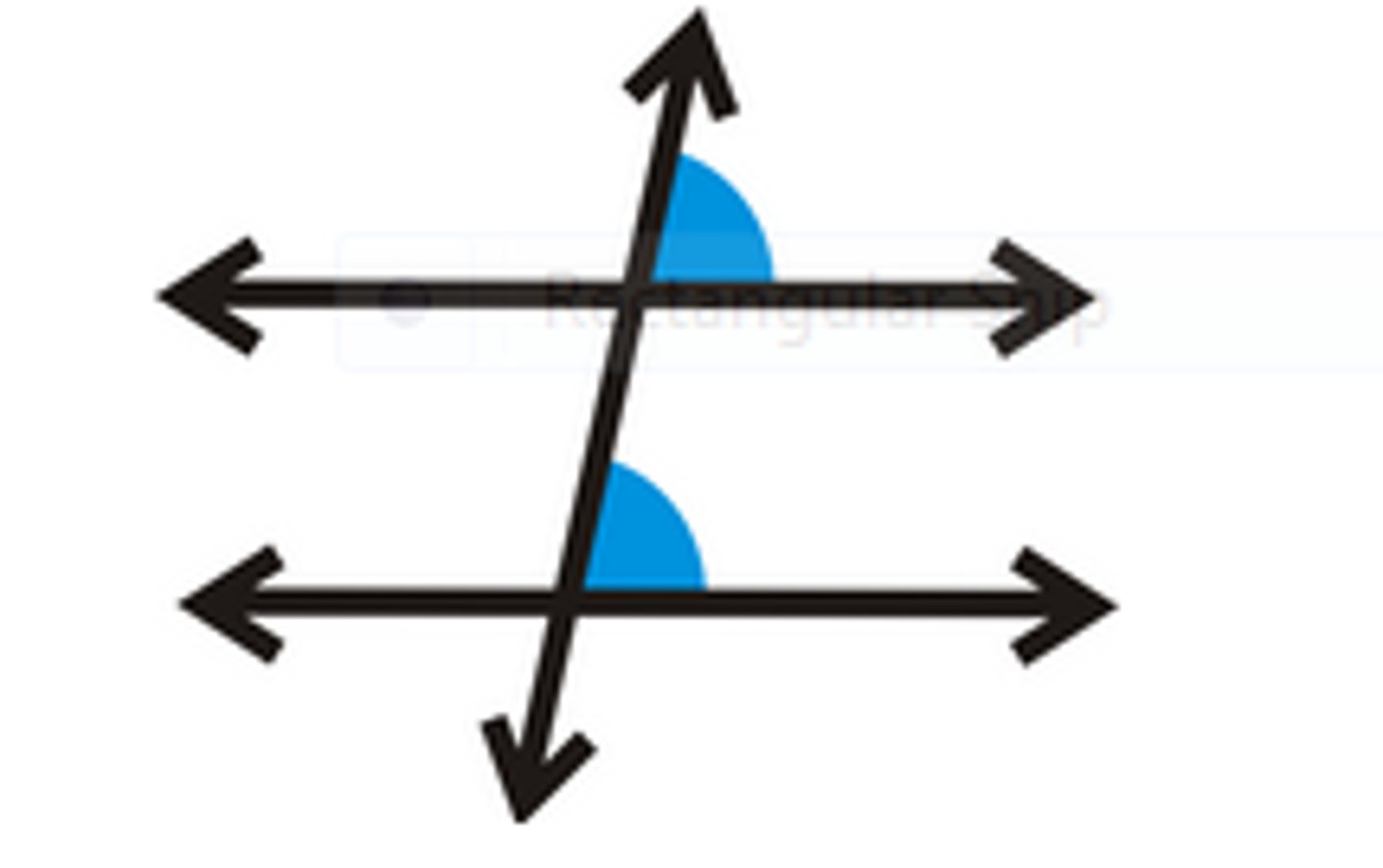
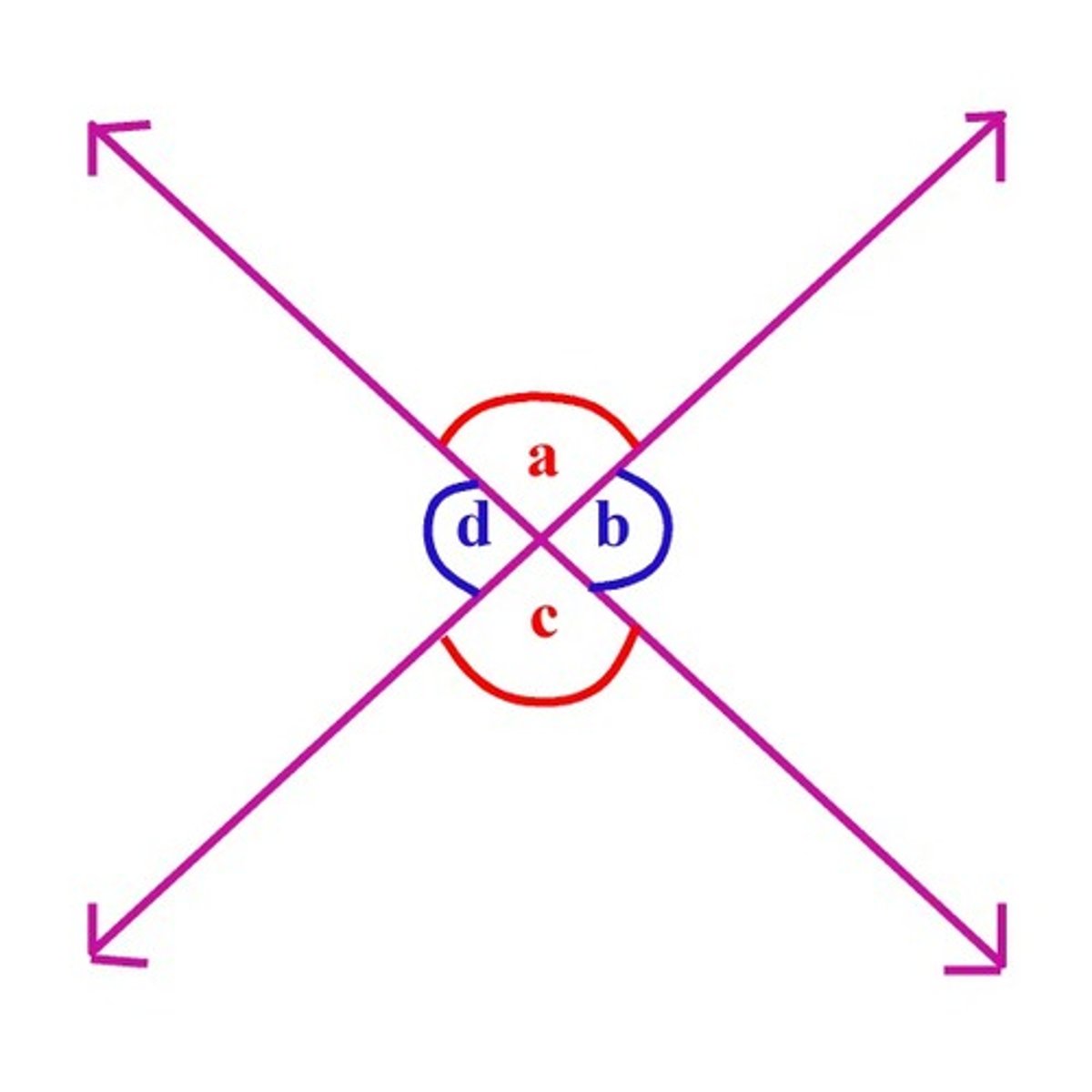
vertically opposite angles

Interior angles.

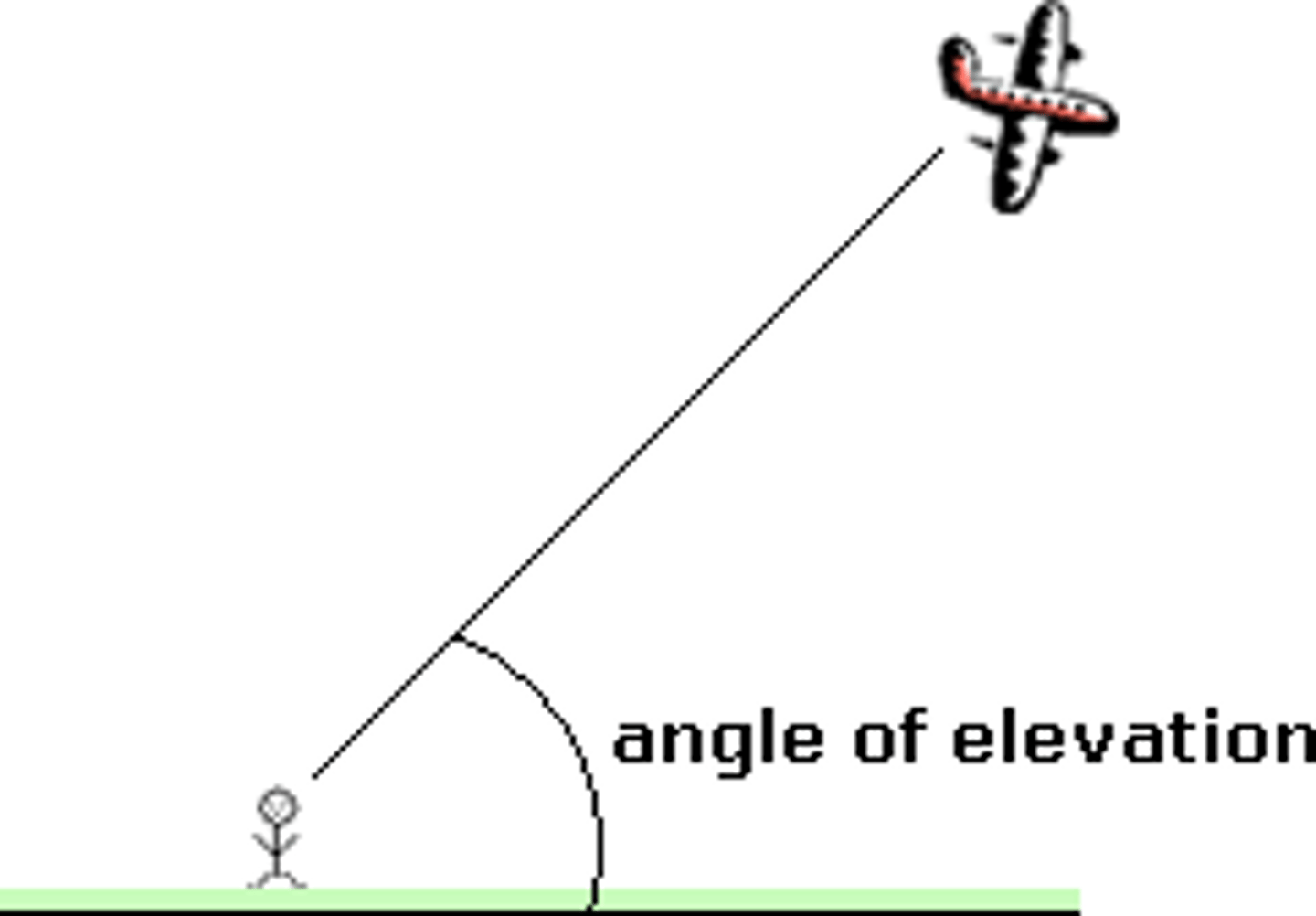
angle of elevation

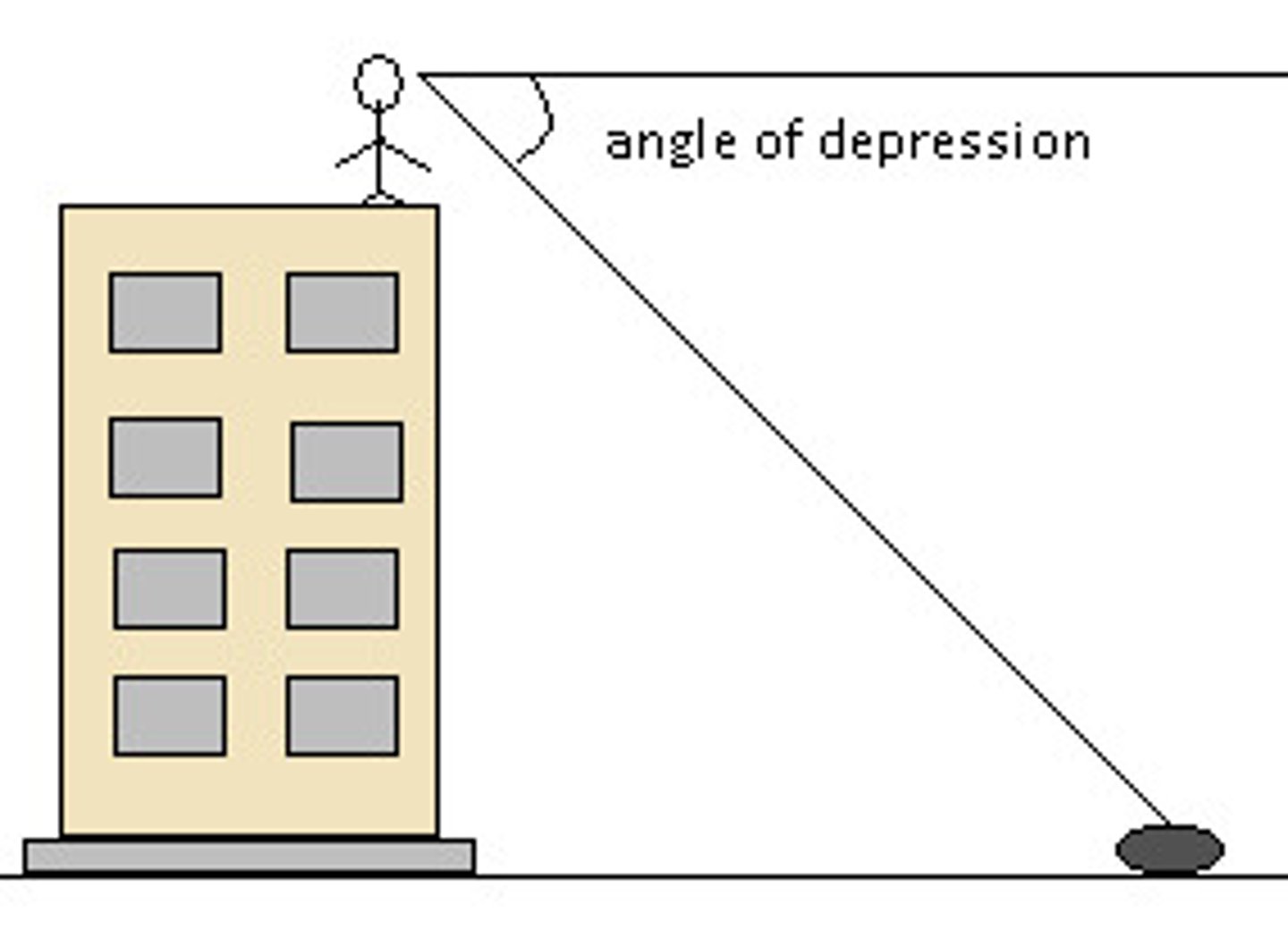
angle of depression

m(x-x1) = y-y1
y= mx + c
ax + by + c = 0

straight line graphs

2 x intercepts - factorise + solve
y- intercept -> value when x=0
turning point -> in a completed square form
(x + a)^2 + b -> (-a,b)
line of symmetry = x = -a

quadratic graphs

exponential graphs
y = a^x
always positive

x^2 + y^2 = r^2

circle equation

no bias
same chance of being chosen
d = time consuming
a = no bias

random smapling

every nth one
a = less time consuming
d = cant be used in certain situations

stratified sampling

representative of relevant subgroups
fraction of population * class width

Stratified sampling

representing the entire population

sampling

3-4-5, 5-12-13, 8-15-17, 7-24-25

pythagorus triplets

frequency/class width

frequency density

start of interval + (number wanted/frequency) * class width

histogram equation

congruency rules

SSS, SAS, ASA, RHS

similarity rules

AA, SAS, SSS

relative frequency

the fraction or percent of the time that an event occurs in an experiment
count of outcomes/number of outcomes

when you have n objects and what to choose r of them ->possibilities

n!/(n-r)!

number of possibilities when you want to choose r of them in different arrangemnets and the option is not removed

n^r

calcutating the number of ways to select r objects from a group of n objects

ncr button

cosine rule

a2 = b2 + c2 - 2bc cos A

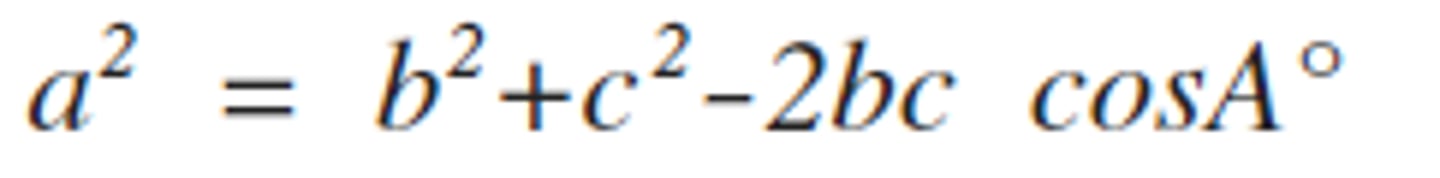
sine rule

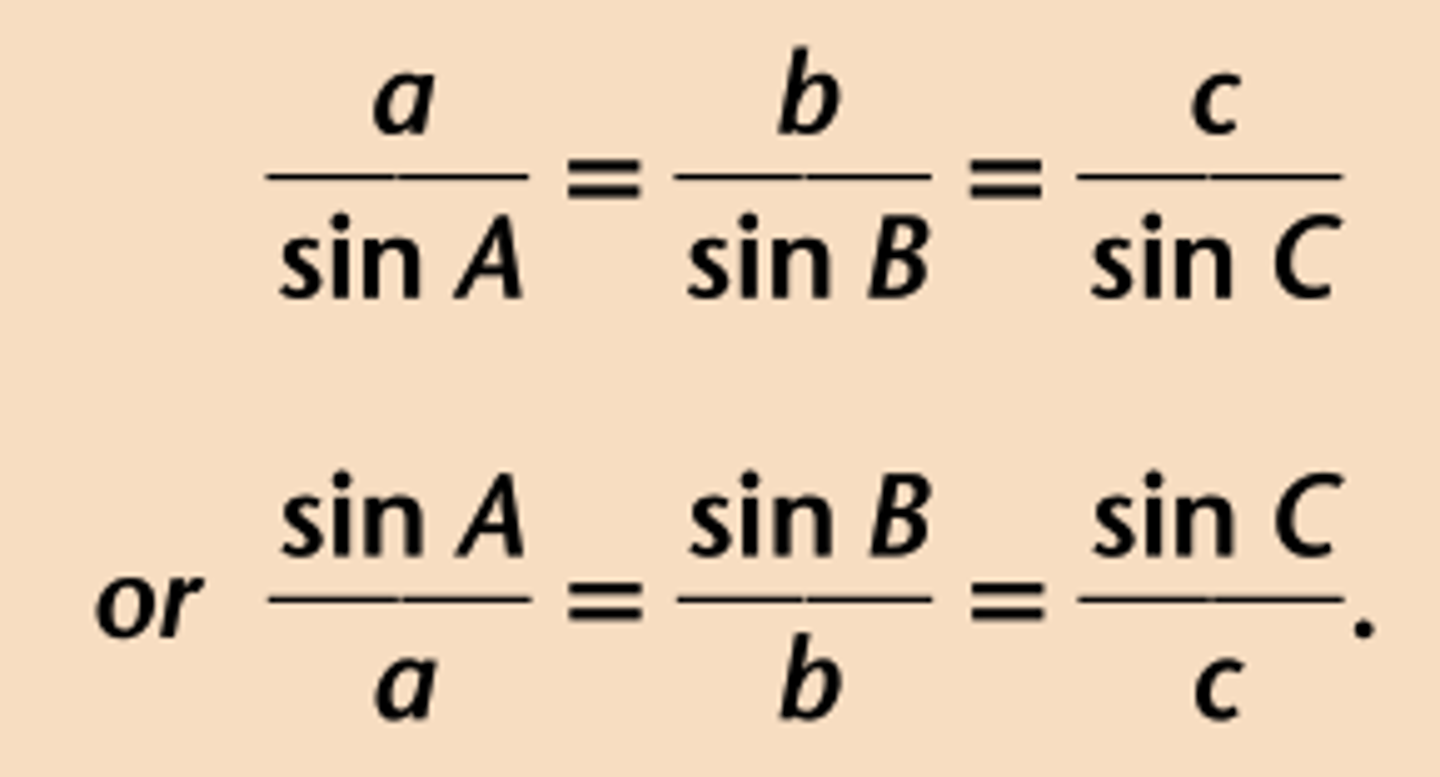
sin^2(x)

(sinx)^2

tan

sin/cos

Cos and Sin Identity

cos^2x + sin^2x = 1
cos can be diveded cause it can never be 0
can never divide out by an other trig function

transformations of functions

translation = y= f(x-a)+b
[ab]
reflection in the x-axis = -f(x)
reflection in the y-axis = f(-x)

sinx graph

calculator

always truncates

circle theorem for isosceles traingle

base angles of an isosceles triangle are equal + angles in a triangle add up to 180

Derivative of Sin(x) and Cos(X)

cosx
-sinx

Trigonometric Identities

Sinθ/Cosθ = Tanθ
Cosθ/Sinθ = 1/Tan
Cos²θ + Sin²θ = 1
Sinθ = Cos(90 - θ)
Cosθ = Sin(90 - θ)

iteration

iteration is an estimation of a solution

frequency polygons

mid point

cumulative frequency

end point

show that the solution is between 0 and 1

theres a sign change

Show that f(x) is odd

Show that f(-x) = -f(x). This shows that the graph of f is symmetric to the origin.

max using diffrentation

dy/dx = 0

sin

180-x

tanx

180+x

cosx

x =-x

domain terminology

the function is not defined at x= something

point of inflection

on each side they are positive

use differentiation to work out the max value of A as x varies

dy/dx = 0