IB Physics SL (Topic C)

oscillation

Periodic back and forth motion.

equilibrium position

The position where the object would rest if all energy was removed from the system.

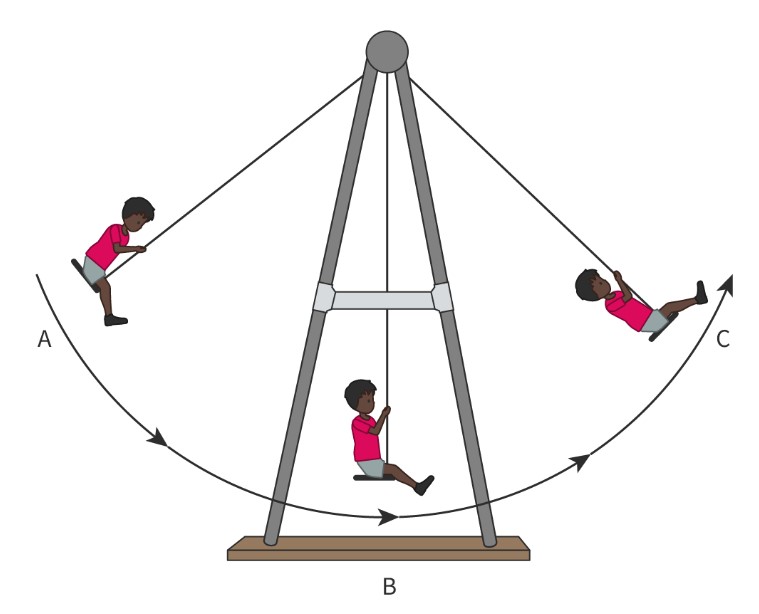
amplitude

The distance between the crest (or trough) of a wave and its equilibrium position. Amplitude is dependent on the magnitude of the initial displacement. Greater mass on the end of spring means lower equilibrium point

time period

The time taken to complete a full cycle. Measured in seconds, inverse of frequency.

• T = timer period (s)

• f = frequency (Hz)

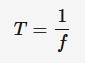
frequency

The rate at which something occurs over a particular period of time or in a given sample. In other words number of cycles completed per second, inverse of time period. Measured in hertz (Hz)

• T = timer period (s)

• f = frequency (Hz)

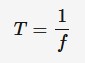
Angular frequency

The angle covered by a simple harmonic motion oscillator per second. In one time period, T, an oscillator will complete one full cycle, or 2pi radians.

• T = time period (s)

• w = angular frequency (rads*s^-1)

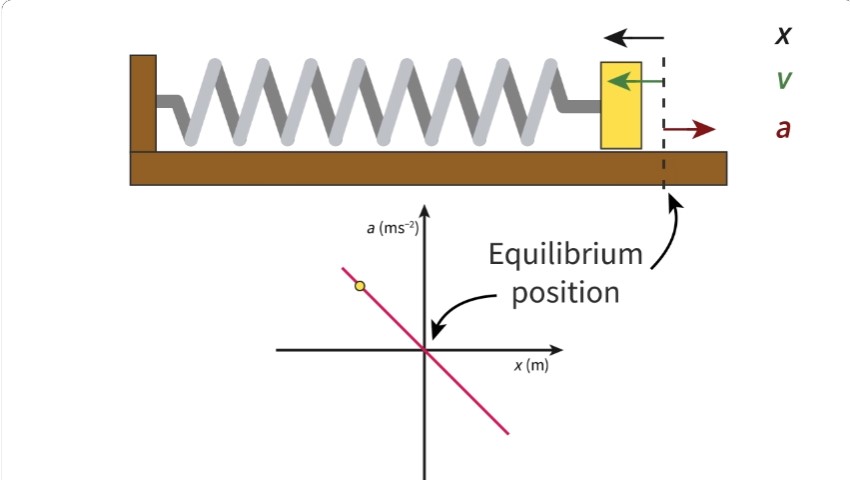
Simple harmonic motion

Oscillations around an equilibrium position where the displacement is proportional to the negative acceleration.

• because acceleration and displacement are in opposite directions, it is negative.

• w = angular frequency (rads*s^-1)

• x = displacement (m)

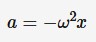
Time period of pendulum

The only factors that affect the time period of the pendulum are the length of the pendulum and the gravity. Time period is independent of mass and amplitude(for smaller angles)

• l = length of pendulum (m)

• g = gravitational force (m*s^-2)

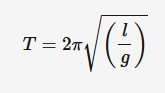
Time period for a mass-spring system

The only factors that affect the time period of the mass-spring system are the mass and the spring constant. Amplitude and gravity do not affect the time period.

• T = time period (s)

• m = mass (kg)

• k = spring constant (N*m^-1)

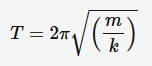
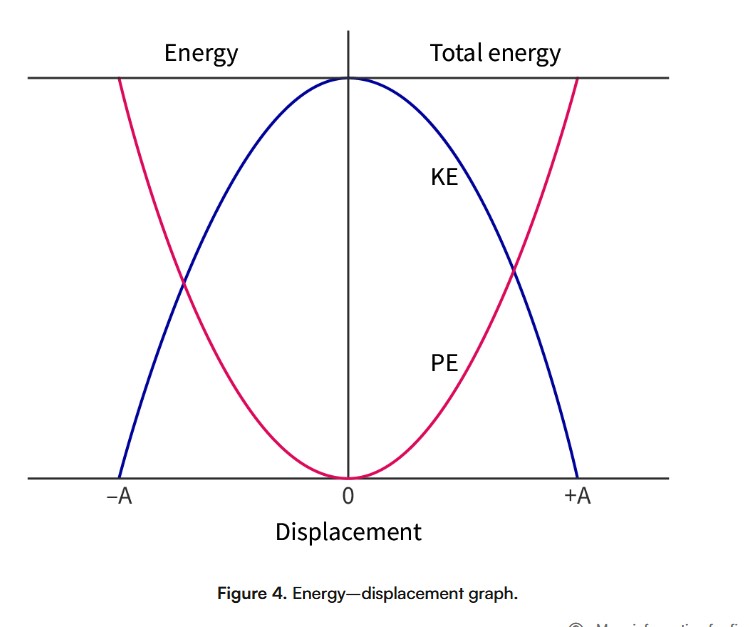
Energy of SHM

When the pendulum is at the peak of its path (maximum displacement), all of its energy is gravitational potential energy. When the pendulum is at the equilibrium position, all of this energy has been transferred to kinetic energy.

For a horizontal mass–spring system, the potential energy is elastic potential energy, but the same transfer to kinetic energy occurs.

For a vertical mass–spring system, the potential energy is gravitational potential energy and elastic potential energy at the top, and elastic potential energy at the bottom. But the general principle still applies.

mechanical waves

A wave that needs a medium to travel through. For example water waves, sound waves, waves in ropes, and seismic waves.

Wave

Is an oscillation that transfers energy but not matter.

longitudinal waves

A wave whose particles oscillate parallel to the direction of energy transfer. Regions where particles are closer together are called compressions and where the particles are more spread out they are called rarefractions.

transverse waves

A wave whose particles oscillate at right angles to the direction of energy transfer. Crest of a transverse wave is at the top and the trough is the lowest point.

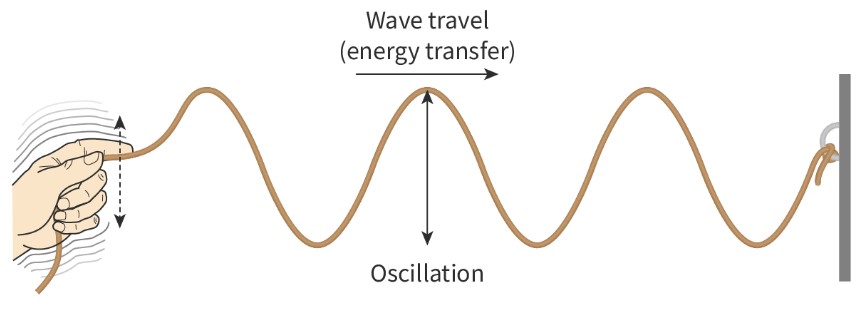
wavelength

The distance between adjacent identical points on a wave, for example, two crests or two compressions.

equation for speed of a wave

v = wave speed (m*s^-1)

^ = wavelength (m)

T = time period (s)
 

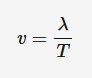
alternate wave speed equation

v = wave speed (m*s^-1)

f = frequency (Hz)

^ = wavelength (m)

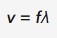
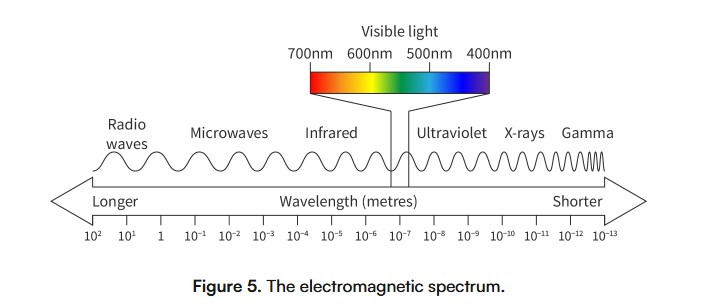
electromagnetic waves

An oscillation in electric and magnetic fields. It is not a mechanical wave and does not need a medium to travel through. They are oscillations in the electric and magnetic fields, the two fields are at right angels at one another.

• important distinction, the frequency of the electromagnetic wave determines the energy per photon while the amplitude determines how many photons are in the wave. High amplitude = more energy, doubling amplitude 4x the energy, high amplitude visible light is brighter
  

reflection

A wave encounters a boundary between two different media and bounces back. The angle of reflection is equal to the angle of incidence.

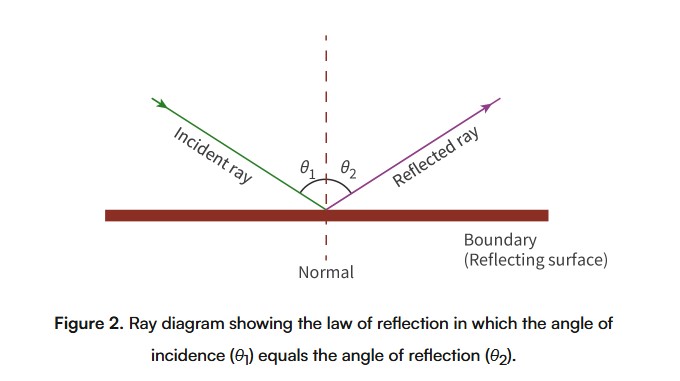
angle of incidence

the angle between the incident wave and the normal to the surface)

angle of reflection

the angle between the reflected wave and the normal to the surface

wave-front diagrams

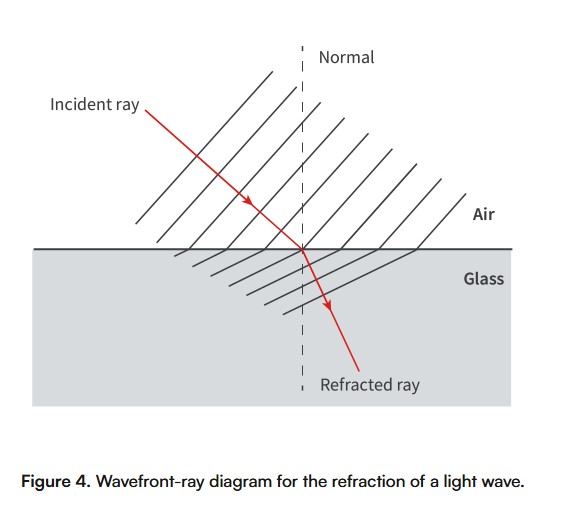
refraction

The change in direction of a wave when it moves from one material to another at an angle, due to the difference in velocity of the waves in the two materials.

• in glass the wave fronts are closer together than the wave fronts in air.

• wavelength decreases as it moves from air to glass, this change is a direct result of the change in speed of the wave.

• frequency does not change when it refracts (frequency is a property of the source of light)

• decrease in wave speed means a decrease in wavelength and vice versa

• the change in speed is what causes the change in direction, different parts of the wavefront are slowed/sped by different amounts as they enter the new medium

• The change in wave speed is due to differences in physical and molecular properties between the two media. 

• usually shorter wave lengths are refracted more(violet)

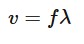
Transmission

When a wave passes across a boundary between two different media and continues to travel through the new medium.

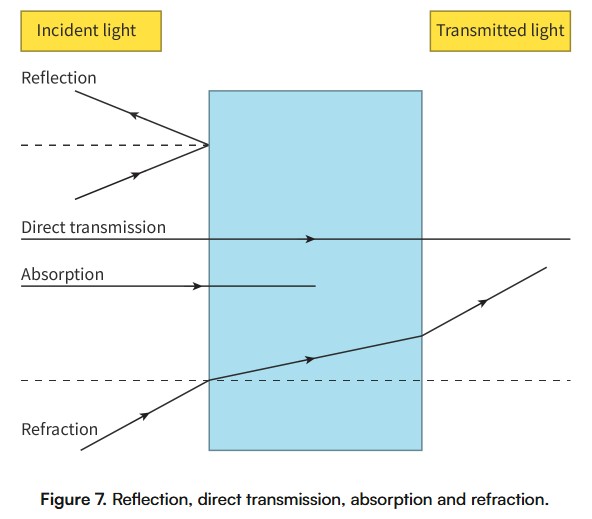
diffraction

The spreading of waves as they travel around a body or through an aperture.

• The extent of diffraction depends on the size of the opening in relation to the wavelength of the waves.

• More specifically, diffraction is more evident when the wavelength is greater than (or similar to) the size of the opening

• visible light waves have much shorter wavelengths (and higher frequencies). So, visible light does not diffract through the door gap, at least not significantly enough for us to notice.

refractive index

A measure of how much a medium can slow down light waves. The ratio of the speed of light in a vacuum to the speed of light in the medium.

• n = the refractive index of the mediu

• c = speed of light in vacuum (3.00 × 10^8 meters per second)

• v = speed of light in the medium in meters per second

greater the refractive index of a medium the more it slows light and the more it is bent. ranges from 1 in a vacuum to over 2 in a diamond.

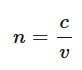
Snell’s law

An equation that describes the angle of incidence and angle of refraction as light (or other waves) is refracted through a boundary between two media that have different refractive index.

• n1 = refractive index of 1st medium

• n2 = refractive index of 2nd medium

• θ1 = angle of incidence (degrees)

• θ2 = angle of refraction (degrees)

• v1 = speed of wave in first medium (m*s^-1)

• v2 = speed of wave in 2nd medium (m*s^-1)

  
  

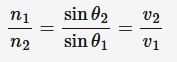
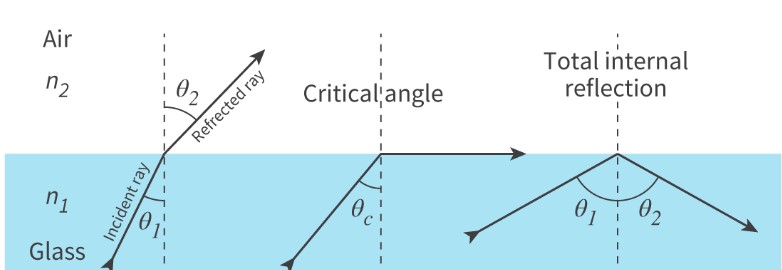
critical angle

The angle of incidence at which light is refracted along the boundary between a medium with a greater refractive index and a medium with a smaller refractive index.

• sinθc = critical angle

• n1 = refractive index of the first medium, n2 = refractive index of the second medium.

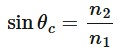
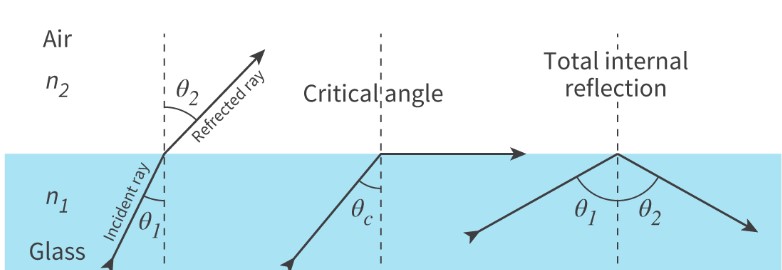
total internal reflection

When the angle of incidence is greater than the critical angle at the boundary between a medium with a greater refractive index and a medium with a smaller refractive index. Light is completely reflected back into the medium with the greater refractive index.

• The light must be passing from a medium with a higher refractive index into a medium with a lower refractive index.

• The angle of incidence must be greater than the critical angle.

superposition

Two waves meet and their displacements add together at every point in space to produce a combined wave with a resultant displacement.

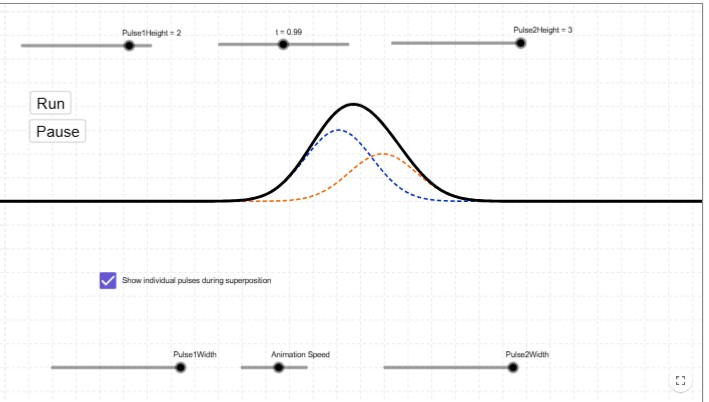
constructive interference

Occurs when two waves meet in phase (crests meet crests and troughs meet troughs), resulting in a wave with increased amplitude.

• To determine the displacement of the resultant wave, we add together the displacements of the individual waves.

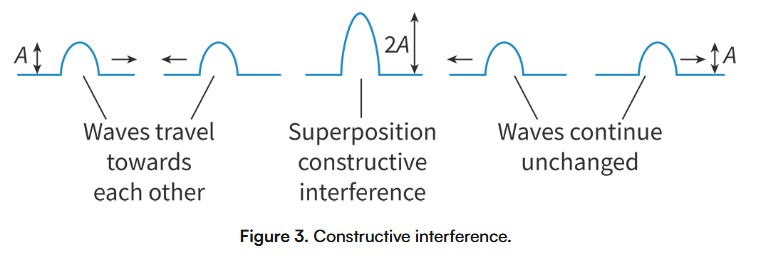
destructive interference

Occurs when two waves meet out of phase (crests meet troughs), resulting in a wave with decreased or zero amplitude.

• To determine the displacement of the resultant wave, we subtract the displacements of the individual waves.

path difference

The difference in distance that two waves travel from a source to a given point.

• measured in amount of wavelenths traveled

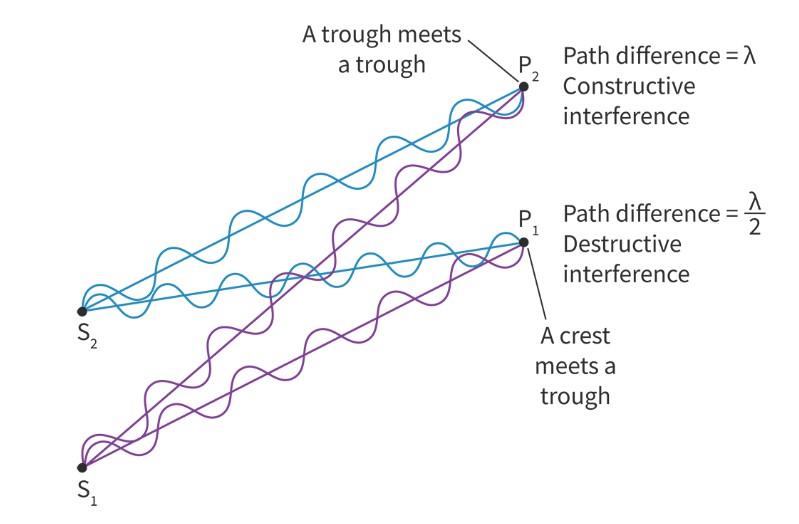
Double source interference

We can see from Figure 6, that the two sound waves interfere constructively and destructively at different points. This is because of the path difference at that point between the waves:

• If path difference is n⁢λ, then the waves interfere constructively.

• If path difference is  (n+12)⁢λ, then the waves interfere destructively.

For sound waves, constructive interference means the sound get louder (greater amplitude), and destructive interference means the sound gets quieter (smaller amplitude). This is why if you move around in a movie theatre, the volume of the sound may appear to fluctuate.

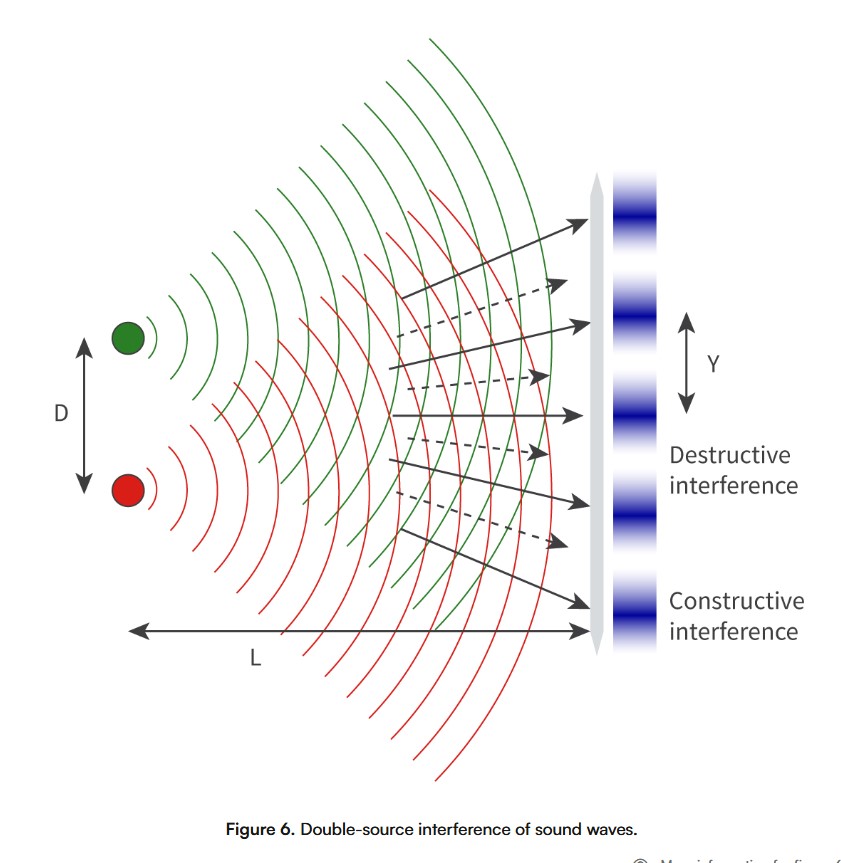
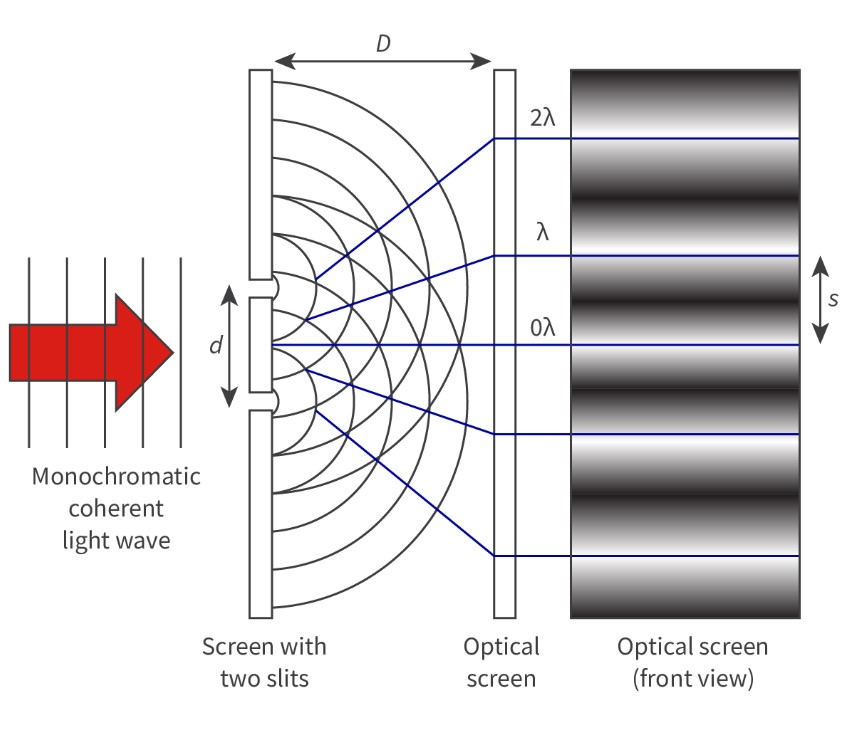
Young’s double slit interference

provided evidence for the wave nature of light and laid the foundation for our understanding of wave interference.

In the double-slit experiment, a monochromatic coherent light source (such as a laser) emits light waves towards a screen with two narrow slits. When the light waves pass through these slits, they act as two coherent light sources. The light waves interfere, creating an interference pattern on the optical screen. The interference pattern consists of alternating dark and light fringes (bands)

The light fringes (maxima) are where the light waves interfere constructively and the dark fringes (minima) are where the light waves interfere destructively.

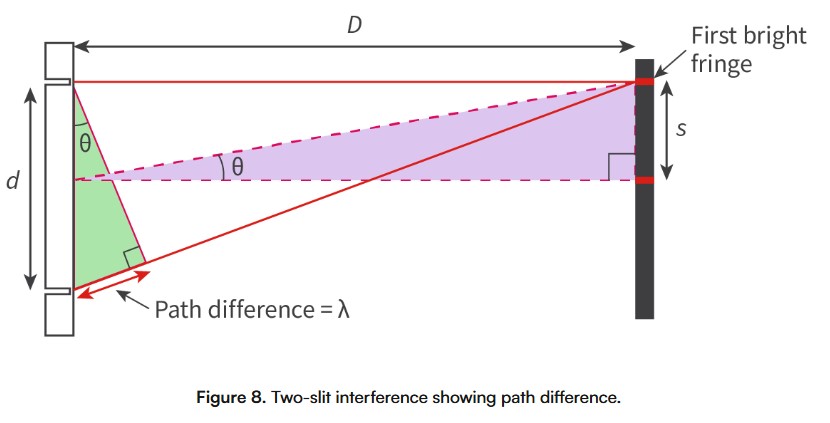
Separation of fringes in double slit experiment

s = separation of fringes (m)

^ = wavelength (m)

D = distance from slits to screen (m)

d = separation of slits (m)

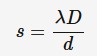
Standing wave

In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space.

• points of maximum displacement are known as antinodes, points of zero displacement are known as nodes

• From Interactive 1, we can see that the nodes and antinodes do not move along the wave, but always stay in the same horizontal position, with the antinodes only oscillating vertically. This is a characteristic of standing waves. 

• When points are in phase that means they got up together, when points are in antiphase that means their displacements are opposite

(go to kognity to watch interactive 1, if you do not understand)

Standing waves in strings

boundary conditions- The conditions at the ends of a string or pipe. For a string, an end can be fixed or free. For a pipe, an end can be open or closed.

The general equation for wavelength

^n= 2L/n

^n = wavelength (m)

L = Length (m)

n = harmonic (first, second, etc)

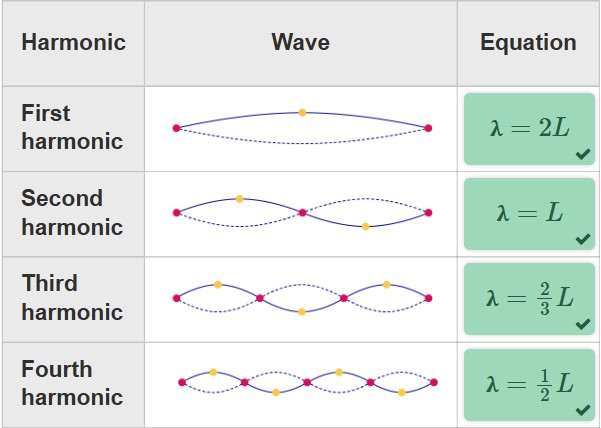
Standing waves in pipes

come back to this later it dont make sense lol

wavelength in an open-closed pipe

^n = 4L/n

^n = wavelength (m)

L = length (m)

n = harmonic (first, third, etc)

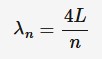
Natural frequency

The frequency at which a system vibrates or oscillates when it is disturbed.

Resonance

when an oscillating system is forced to vibrate close to the frequency at which it would vibrate naturally.

dampening

Techniques used to restrain and reduce oscillations and vibrations.

driving frequency

The frequency of the oscillator supplying energy to the system.

resonant frequency

The frequency at which the oscillations of an object gain the greatest amplitude.

Light damping

There is a small amount of damping only. The system will continue to oscillate, but the amplitude of the oscillations decreases exponentially over time.

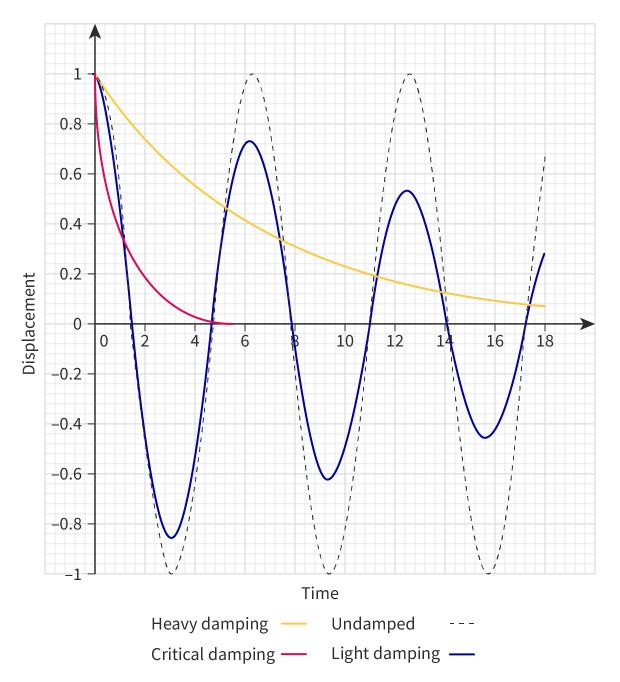
Heavy damping

There is a large amount of damping. The system gradually dissipates all its energy. It does not oscillate, but returns very slowly to its equilibrium state.

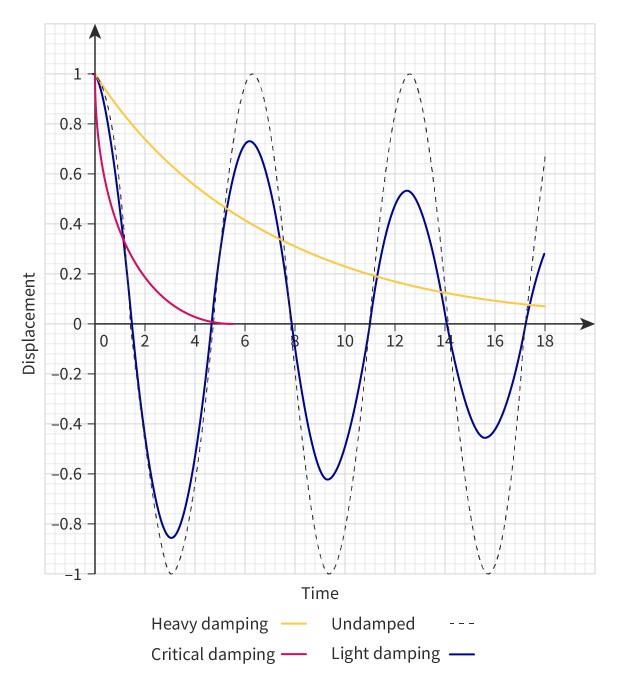
Critical dampening

There is a very large amount of damping. The system returns to its equilibrium state as quickly as possible without any oscillations.

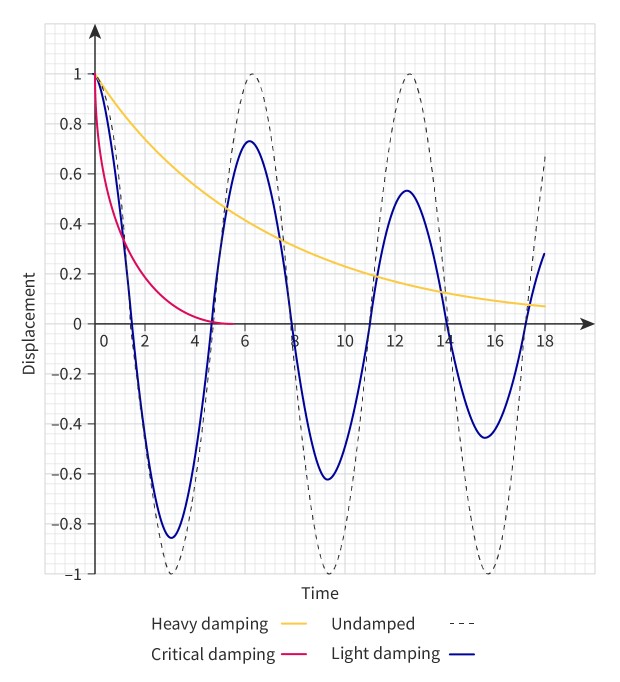
Effect of damping on an oscillator

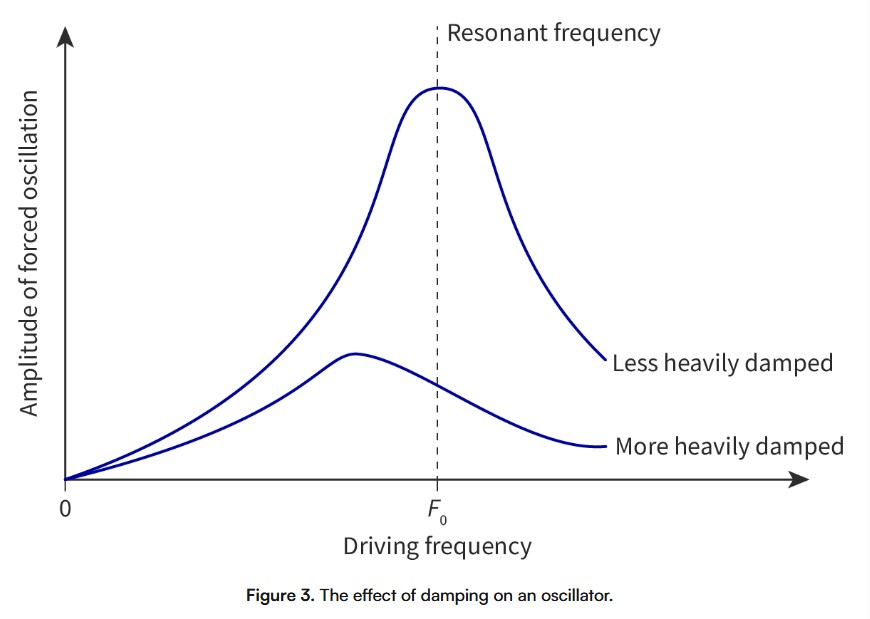
Damping changes the frequency of an oscillator. As damping is increased, the resonant frequency decreases, and the amplitude decreases (Figure 3). Since T=1/f (subtopic C.1), the time period increases.

GO over doppler