Chem Ch. 6

Atomic weight

The average mass of an element's naturally occurring isotopes

What is the atomic weight of Carbon?

12.011 amu

Molecular weight

The average mass of a substance's molecules

What is the molecular weight of H2O

H = 1.0078 (2)

O = 15.999

Molecular weight = 18.0146

Moles

Amount of substance needed for each subatomic particle to have a mass of 1g

Molar mass

Mass in grams of 1 mole of a substance

= to molecular weight

Unit for molar mass

g/mol

Avogadro's number

# of particles in 1 mol of substance

Avogadro's number examples

1 mole of oxygen atoms (O) = 6.022 × 10²³ oxygen atoms

Molecules Example:

1 mole of water (H₂O) = 6.022 × 10²³ water molecules

1 mole of Na⁺ ions = 6.022 × 10²³ sodium ions

🔹 Simple Way to Think About It

Just like 1 dozen = 12 items,

1 mole = 6.022 × 10²³ particles

What is avogadro's number

6.022 x 10^23

How to use avogadro's number example:

How many copper atoms are in 2.45 mol of copper?

2.45 mol * 6.022 x 10^23 / 1 mol = 1.41 x 10^24 particles

Subscript vs. coefficient

Subscript → number of atoms in one molecule

- ex. In H₂O, the subscript 2 means there are 2 hydrogen atoms in each molecule of water.

Coefficient → number of molecules (or moles) of that substance

- In 2H₂O, the coefficient 2 means there are 2 molecules (or 2 moles) of water.

Total atoms: 2×(2H+1O)=4H+2O

Hydrolyzing water example: 2H2O --> 2H2 + O2

- Every 2 mols of water will be broken down bro 2 molecules of H and 1 molecule of O

- the COEFFICIENTS describe ratios

- mol-mol conversions are carried out using these ratios as conversion factors

- Coefficient = ratio

- 2:1 ratio

4 steps for determining mass relationships among reactants and products

1. BALANCE!!!!!!

2. Choose molar masses and mole ratios to convert the known info into the needed info

3. Set up factor-label expression

4. Calculate answer

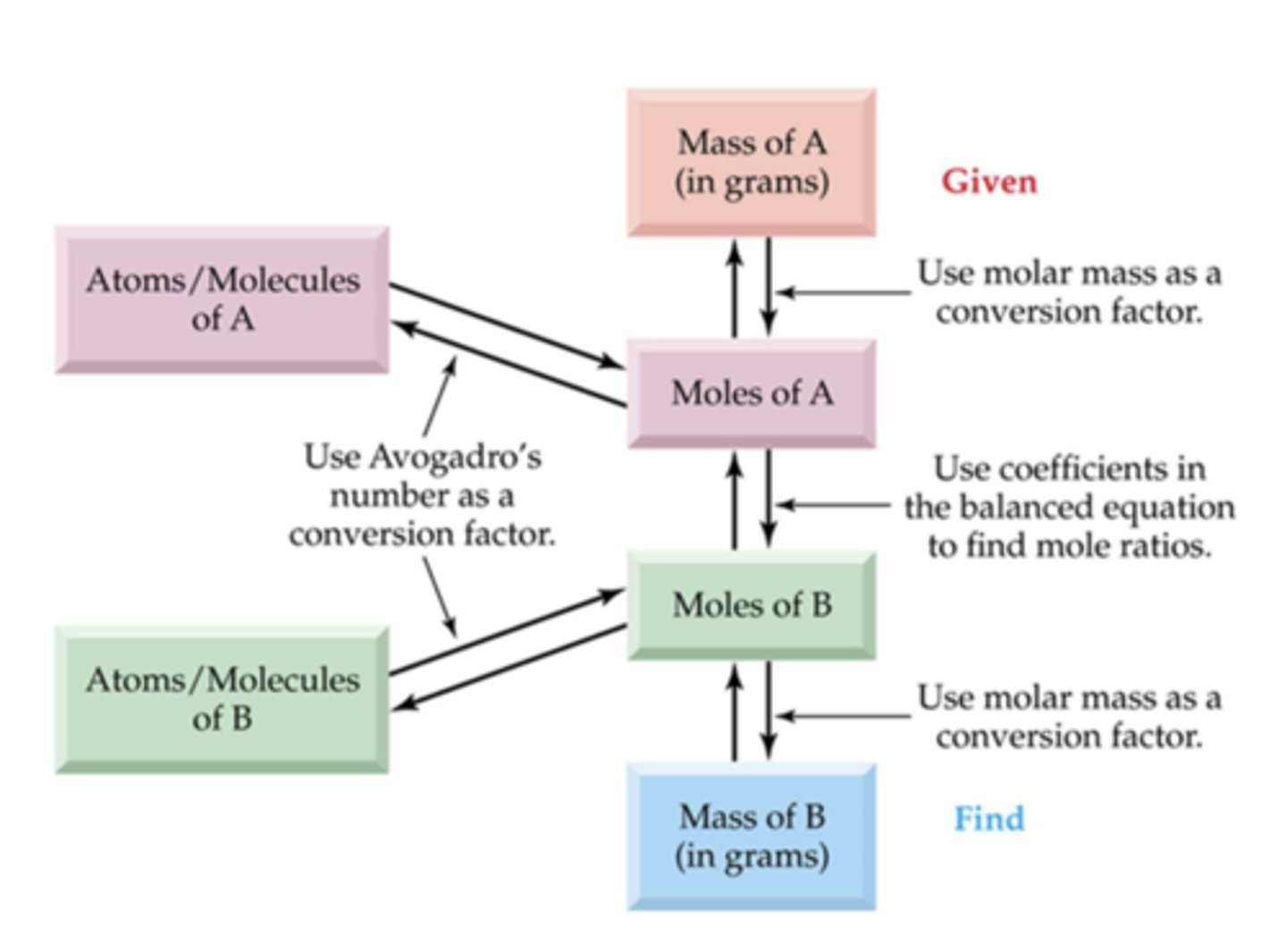
Step 1 to determining mass relationships among reactants and products example:

How many grams of CO₂ form when 25.0 g of propane (C₃H₈) burns completely in excess O₂?

Balance the equation:

Unbalanced: C₃H₈ + O₂ --> CO₂ + H₂O

Balanced: C₃H₈ + 5 O₂ → 3 CO₂ + 4 H₂O

Step 2 to determining mass relationships among reactants and products example:

How many grams of CO₂ form when 25.0 g of propane (C₃H₈) burns completely in excess O₂?

Choose conversion factor (diagram path):

We start with mass of A (C₃H₈) and want mass of B (CO₂).

Path: mass A → moles A → moles B → mass B

Molar mass C₃H₈ = 44.097 g/mol

Molar mass CO₂ = 44.009 g/mol

Mol ratio (from coefficients):

3 mol CO2 / 1 mol C₃H₈

3: 1 ratio

Step 3 to determining mass relationships among reactants and products example:

How many grams of CO₂ form when 25.0 g of propane (C₃H₈) burns completely in excess O₂?

Set up factor-label expression:

25 g CO₂ = 1 mol C₃H₈ / 44.097 g C₃H₈ 3 mol CO₂ / 1 mol C₃H₈ 44.009 g CO₂ / 1 mol CO₂

Notice how grams cancel → moles cancel → grams of CO₂ remain

Step 4 to determining mass relationships among reactants and products example:

How many grams of CO₂ form when 25.0 g of propane (C₃H₈) burns completely in excess O₂?

Calculate:

Result ≈ 74.9 g CO₂ (3 significant figures)

How does the example problem match the diagram?

Mass of A ↔ Moles of A: used molar mass of C₃H₈

Moles of A ↔ Moles of B: used coefficients (1→3)

Moles of B ↔ Mass of B: used molar mass of CO₂

Reaction example to find ratio: A + 2B --> C

Find the ratio

Every mol of A --> requires 2 mols of B to react

Ratio: 1: 2

Imagine you have 2A and 2B with the 2: 1 ratio, what will happen?

the 2B reacts with 1A and runs out, stopping the reaction → leaves 1 mol A in excess.

Limiting reagent

The reactant that ran out first - causing the reaction to stop

What is the limiting reagent from the example: 1A + 2B = C with 2 mols of A and 2 mols of B available

1. Identify the ratio

2. Set up an equation to identify the limiting reagent

2 mol A * 2 mol B / 1 mol A = 4 mol of B needed

B will run out first

Limiting reagent: B

Excess reagent

The reagent that has amount left over (in excess)

What is the limiting reagent from the example: 1A + 2B = C with 2 mols of A and 2 mols of B available

1 mol of A is left in excess

Excess reagent: A

Theoretical yield (calculated)

In theory how much product formed by the time the limiting reagent ran out when you calculate it

Actual yield

How much was collected when the experiment is carried out in the lab

Percent yield equation

% yield = actual/theoretical x 100 (in percentage)

Easy way to find limiting reagent problems

Use a RICF table (ratio, initial, change, final)

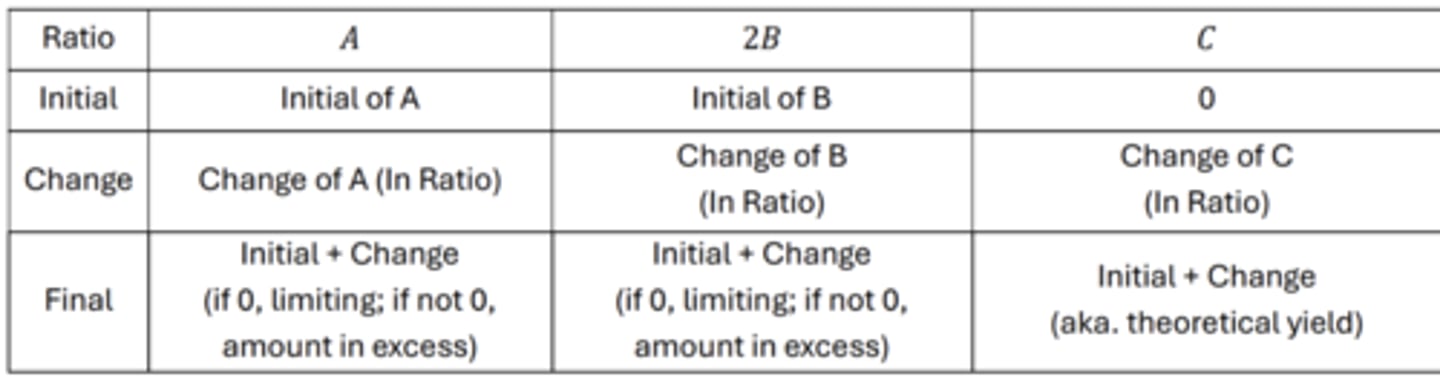
Notes for RICF table

- only input mols

- at least one of the reactants should have 0 mol for final (limiting reagent)

Example of how to use a RICF table:

Calculate the mass of Mg oxide possible if 2.4 g Mg reacts with 10 g of O2

2Mg + O2 → 2MgO

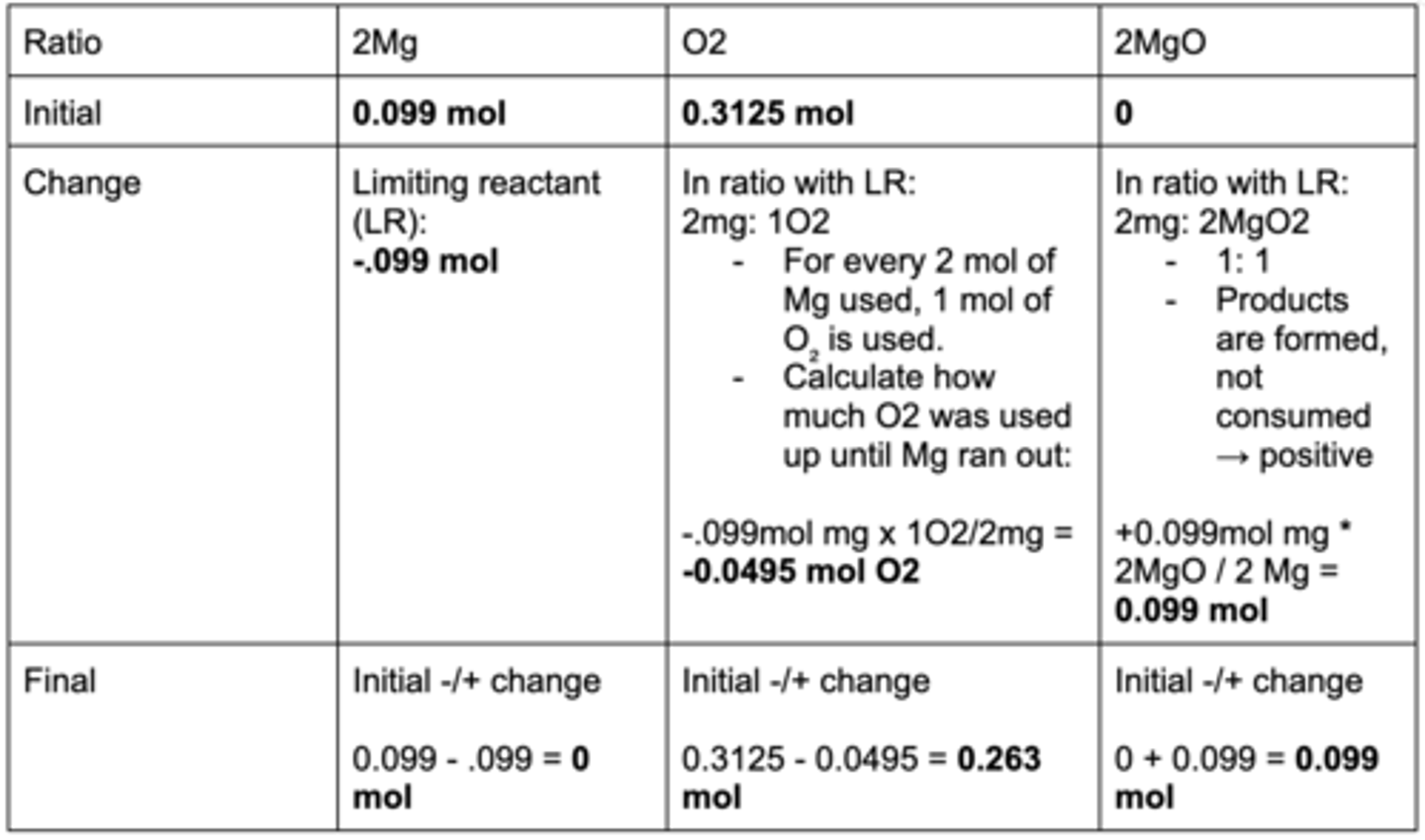
Shown in chart:

Limiting reactant (mol) - Mg

Excess amount (mol) - O2

Theoretical yield for (mol) - MgO; can be converted to mass

0.099 mol x 40.3g/mol = 3.99g

Calculating percent and actual yield from the example

Assume percent yield/recovered is 75%

Know which chemical we are dealing with: FIRST ROW PRODUCT (MgO)

Calculate actual yield:

% yield = Actual/theoretical x 100%

.75 = actual / 0.099

Actual = 7.4% OR 0.07425 mol

Convert to mmol:

1 mol = 1000 mmol

0.07425 mol / 1 * 1 mmol/10^3 mol = 74.24 mmol

Or convert to mass:

0.07425 mol / 1 * 40.4g/mol = 2.99 g