Combined Final Exam Memorization

From Exam 1 to Exam Final

Colinear Definition & Formula (For Points P, Q, R)

\overrightarrow{PQ} \parallel k \cdot \overrightarrow{PR}

• Colinear: When three points lie on a straight line

Two 3D Vectors are Colinear if

Their Cross Product is a zero vector

Dot Products are useful for

1. Finding the angle between two vectors

2. Vector Projection

3. If dot product of two vectors is 0, vectors are perpendicular (orthogonal)

Dot Product Formulas

1. Geometric: |\vec{A}| |\vec{B}| \cos(\theta)

2. Algebraic: A_x B_x + A_y B_y + A_z B_z (Use for angle determination)

Angle between two vectors formula

\cos^{-1} \left( \frac{\vec{A} \cdot \vec{B}}{|\vec{A}| |\vec{B}|} \right) (uses non-geometric = geometric dot product formulas)

Projection Formula

\text{proj}_{\vec{a}}\vec{b} = \frac{\vec{a} \cdot \vec{b}}{\vec{b}\cdot\vec{b}} \vec{b}

Cross Product Formulas

1. Geometric: |\vec{A}| |\vec{B}| \sin(\theta)

2. Algebraic: Use the matrix —>i |i_{\text{matrix}}| - j |j_{\text{matrix}}| + k |k_{\text{matrix}}| (see image)

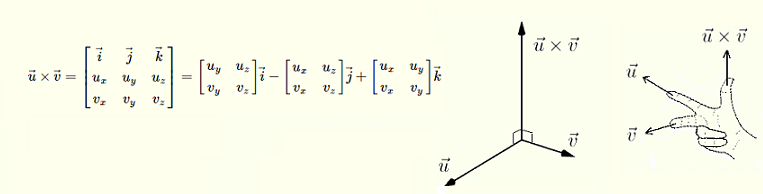
Scalar Triple Product Formula

(\vec{u} \times \vec{v}) \cdot \vec{u} = 0

Area between two functions

\int_{a}^{b} [f(x) - g(x)] \, dx (Where f(x) is on top of g(x))

Washer & Shell Method Formulas

1. Washer: \pi \int \left[ (R_{\text{outer}}(x))^2 - (R_{\text{inner}}(x))^2 \right] \, dx

2. Shell: 2\pi \int_{a}^{b} |x-h| \cdot f(x) \, dx

   1. h is axis of rotation

   2. Remember that abs |x-h| = (h-x) usually

When to use Washer / Shell

• X-axis (horizontally): Washer in dx, Shell in dy

• Y-axis (vertically): Washer in dy, Shell in dx

Length of a curve formula

\int_{a}^{b} \sqrt{1+\left( \frac{dy}{dx} \right)^2} dx

Surface Area Formula

2\pi \int_{a}^{b} f(x) \sqrt{1 + \left( f'(x) \right)^2} dx

Work Done by a Spring (Hooke’s Law)

1. F = kx

   1. \int_{a}^{b} kx dx = \frac{1}{2}k(b^2 - a^2)

Work Done by Pulling a Cable

\int_{0}^{L} \rho g y A(y) dy

Work Done by Pumping Water Out

\int_{a}^{b} \rho g d(x) A(x) dx

Integral of -\frac{1}{x\sqrt{x² - 1}}

arccsc x + C

Integral of ln(ax)

x ln(ax) - x

Double Angle Identity for \sin(2x)

2\sin(x)\cos(x)

Double Angle Identity for \cos(2x) (Three Answers)

1. \cos^2(x) - \sin^2(x)

2. 1 - 2\sin^2(x)

3. 2\cos^2(x) - 1

Double Angle Identity for \tan(2x)

\frac{2\tan(x)}{1 - \tan^2(x)}

Power Reduction Half Angle Identity for \sin²(x)

\frac{1}{2} - \frac{\cos(2x)}{2}

Power Reduction Half Angle Identity for \cos²(x)

\frac{1}{2} + \frac{\cos(2x)}{2}

Pythagorean Identity for sin and cos

\sin²x + \cos²x = 1

Pythagorean Identity for tan and sec

1 + \tan²x = \sec²x

Integral of tan(x)

\ln|\sec(x)| \quad \text{or} \quad -\ln|\cos(x)|

Integral of csc(x)

\ln|\csc(x) - \cot(x)| \quad \text{or} \quad -\ln|\csc(x) + \cot(x)|

Integral of sec(x)

\ln|\sec(x) + \tan(x)|

Integral of cot(x)

\ln|\sin(x)|

d/dx ln(f(x))

f’(x) / f(x)

d/dx sin(x)

cos(x)

d/dx cos(x)

-sin(x)

d/dx tan(x)

sec²(x)

d/dx cot(x)

-csc²(x)

d/dx sec(x)

sec(x) tan(x)

d/dx csc(x)

-csc(x) cot(x)

d/dx arcsin(ax)

\frac{a}{\sqrt{1-(ax)²}}

d/dx arccos(ax)

-\frac{a}{\sqrt{1-(ax)²}}

d/dx arctan(ax)

\frac{a}{1+(ax)²}

\int \frac{dx}{x² + a²}

\frac{1}{a} \arctan(\frac{x}{a}) +C

d/dx arccot(ax)

-\frac{a}{1+(ax)²}

d/dx arcsec(ax)

\frac{a}{ax\sqrt{(ax)²-1}}

d/dx arccsc(ax)

-\frac{a}{ax\sqrt{(ax)²-1}}

Steps to solve \int \tan^m (x) \cdot \sec^n (x) dx (4 cases)

1. m and n are both even:

   1. take out one factor of \sec²(x) and turn it into 1 + \tan²(x)

   2. U-Sub for u=\tan(x), du=\sec²(x)dx

   3. Integrate in terms of u

2. m (tangent power) odd, n (secant power) even:

   1. Take out one \tan(x) from \tan^m (x)

   2. U-Sub for u=\tan(x), du=\sec²(x)dx

   3. Integrate in terms of u

3. n (secant power) odd, m (tan power) even:

   1. Take out one \sec(x) from \sec^n (x)

   2. U-Sub for u=\sec(x), du=\sec(x)\tan(x)dx

   3. Integrate in terms of u

4. Both m and n are odd:

   1. U-Sub for u=\tan(x)

   2. Integrate in terms of u

Trig Sub For \sqrt{a² - x²}

x = a \sin \theta

Trig Sub For \sqrt{a² + x²}

x = a \tan \theta

Trig Sub For \sqrt{x² - a²}

x = a \sec \theta

Partial Fraction Decomposition (PDF) Conditions

1. Rational Function - Must have polynomial on numerator and denominator

2. Proper Fraction - Degree of numerator MUST be less than degree of denominator (or else long divide)

3. Factorable Denominator - Denominator must factor into linear factors with degree of 1

PFD: (x-4)

Linear: \frac{A}{x-4}

PDF: (x+4)²

Repeated Linear: \frac{A}{x+4} + \frac{B}{(x+4)²}

PFD: (x²+4)

Irreducible Quadratic: \frac{Ax + B}{(x²+4)}

PFD: (x²+4)²

Repeating Irreducible Quadratic: \frac{Ax+B}{(x²+4)} + \frac{Bx+C}{(x²+4)²}

Recursive Sequence

Using previous terms, like the Fibonacci sequence

Explicit Sequence

Each new term is given by substituting the value of n into the formula (Ex: a_{n} = \frac{3^{n}}{n!} )

The limit of the sequence (a_{n} \text{ as } n \rightarrow \infty ) determines if the sequence ______ or ______

converges or diverges

Theorems that might help solve the limit of a sequence are the _________ and/or ________

squeeze theorem, limit laws, L'Hopital's rule, and/or factoring out the dominant term

\lim_{x \to 0} \frac{\sin{x}}{x} =

1 (Use L’Hopital’s rule)

\lim_{x \to \infty} \frac{\sin{x}}{x} =

0

\lim_{x \to 0} x \sin(1/x) =

0

\lim_{x \to 0} \sin(f(x)) =

f(x)

\lim_{x \to 0} \frac{1 - \cos(x)}{x²} =

½ (L’Hopital’s Rule)

\lim_{x\to\infty} -e^{-x}

0

Constants/Exponential/Root Laws for Limits

1. Constant * limit

2. (limit)^power

3. root(limit)

L'Hopital's Rule

• If the limit is indeterminant \frac{0}{0} \text{ or } \frac{\infty}{\infty}

• Then: \lim \frac{f(x)}{g(x)} = \lim \frac{f’(x)}{g’(x)} (repeat until converges)

Factoring Out the Dominant Term (for a_n = \frac{f(x)^n}{g(x)^d} , where n and d are the degrees of the Polynomial)

Divide f(x) and g(x) by x^d, where d is the highest power of x present in the denominator. Then simplify and solve the limit.

• Ex: a_n = \frac{x}{\sqrt{4x² + 2}} \rightarrow \frac{\frac{x}{\sqrt{x²}}}{\sqrt{\frac{4x²}{4x²} + \frac{2}{4x²}}} = \frac{1}{2}

Sequence Limit Definition of e

\lim_{n \to \infty} (1 + \frac{r}{n})^{n} = e^{r+n} (when r = 1 answer is e)

Geometric Sequences

Sequence where each term is = previous term * a common constant ratio of r a_{n} = a_{n-1} \cdot r

How can you find the ratio in a geometric sequence?

r = any term / previous term

Convergence vs Divergence in Geometric Sequences/Series:

1. |r| < 1

2. |r| > 1

3. r = 1

4. r = -1

1. converges to zero

2. diverges to infinity

3. converges to a_1

4. Diverges due to occilation

Factorial Sequences can often be solved using the Recursive Definition n! = ? and (n+3)! = ?

1. n! = n \cdot (n-1) \cdot (n-2) \cdot …

2. (n + 3)! = (n+3)(n+ 2)! …

Monotonicity of sequences

• tells us if a sequence is increasing, decreasing, or neither

• helps us predict if a sequence is approaching a limit in a predictable way

To check if a sequence is increasing, find the _________ between terms. If _______ the sequence is increasing.

find the difference between terms. If positive the sequence is increasing.

(Ex: Sequence a_n = \frac{n}{n+1} \to a_{n+1} - a_n = \frac{n+1}{n+2} - \frac{n}{n+1} = \frac{1}{(n+1)(n+2)} which is positive, so increasing)

Growth Rates of Sequences Theorem

1. Logarithms grow slower than Polynomials

   1. \lim_{n \to \infty} \frac{\ln(n)}{n^p} = 0 for any p>0

2. Polynomials grow slower than Exponentials

   1. \lim_{n \to \infty} \frac{n^p}{a^n} = 0 for p > 0 and a > 1

3. Exponentials grow slower than Factorials

   1. \lim_{n \to \infty} \frac{a^n}{n!} = 0 for a > 1

4. Factorials grow slower than n^n

   1. \lim_{n \to \infty} \frac{n!}{n^n} = 0

5. IMPORTANT: Exponentials grow faster than polynomials.

If a sequence has an upper bound (M) and/or lower bound (m) (m \leq a_n \leq M) for all n, it is _____

bounded

• Can be bounded above (never goes above M)

• Can be bounded below (never goes below m)

• Can be bounded (stays between m and M)

Bounded Monotone Sequence Theorem: If a sequence is bounded and monotonic (always increasing or always decreasing) then the sequence will ______

the sequence will converge

Factorial Sequences will usually ______ unless counterbalanced

diverge unless counterbalanced

• Ex: a_n = n! diverges

• Ex: a_n = \frac{n!}{n^n} converges to 0 since n^n grows faster than n!

• Ex: a_n = \frac{n!}{2^n} diverges since power-tower

For a series (\sum{a_n}) to converge, the sequence must _______ __ _

converge to 0 (\lim_{n \to \infty} a_n = 0)

Infinite Geometric Series sum can be found with this formula:

S_{\infty} = \frac{a_1}{1-r} for |r| < 1

Finite Geometric Serries sum can be found with this formula:

S_n = a_1 \cdot \frac{1-r^n}{1-r}

In Telescoping Series, recognize _______ in terms to solve

repetition since terms will cancel each other out (S_n = \sum_{k=1}^{n} (\frac{1}{k} - \frac{1}{k+2}) \to (1 - \frac{1}{3}) + (\frac{1}{2} - \frac {1}{4}) + (\frac{1}{3} - \frac{1}{5})… = 3/2)

• Often can be found using partial fraction decomposition

For \int_1^{\infty} \frac{1}{x^p} dx when is this p-series convergent / divergent?

Convergent for p > 1, divergent otherwise

\sum_{n=1}^{\infty} \frac{1}{n!} =

e = 2.7…

\lim_{x \to \infty} \sin(\frac{1}{f(x)})

f(x)

\lim_{x \to \infty} \tan(\frac{1}{f(x)})

f(x)

\lim_{x \to 0} \frac{\sin{x}}{x} =

1

\lim_{x \to \infty} \frac{\sin{x}}{x} =

0 (Squeeze theorem)

\lim_{x \to 0} x \sin(1/x) =

0

\lim_{x \to 0} \sin(f(x)) =

f(x)

\lim_{x \to 0} \frac{1 - \cos(x)}{x²} =

1/2

\lim_{x\to\infty} -e^{-x}

0

Factoring Out the Dominant Term (for a_n = \frac{f(x)^n}{g(x)^d} , where n and d are the degrees of the Polynomial)

Divide f(x) and g(x) by x^d, where d is the highest power of x present in the denominator. Then simplify and solve the limit.

• Ex: a_n = \frac{x}{\sqrt{4x² + 2}} \rightarrow \frac{\frac{x}{\sqrt{x²}}}{\sqrt{\frac{4x²}{4x²} + \frac{2}{4x²}}} = \frac{1}{2}

Infinite Geometric Series sum can be found with this formula:

S_{\infty} = \frac{a_1}{1-r} for |r| < 1

Finite Geometric Serries sum can be found with this formula:

S_n = a_1 \cdot \frac{1-r^n}{1-r}

In Telescoping Series, recognize _______ in terms to solve

repetition since terms will cancel each other out (S_n = \sum_{k=1}^{n} (\frac{1}{k} - \frac{1}{k+2}) \to (1 - \frac{1}{3}) + (\frac{1}{2} - \frac {1}{4}) + (\frac{1}{3} - \frac{1}{5})… = 3/2)

• Often can be found using partial fraction decomposition

For \int_0^1 \frac{1}{x^p} when is this p-series convergent / divergent?

Convergent for p < 1, divergent otherwise

\sum_{n=1}^{\infty} \frac{1}{n!} =

e = 2.7…

Divergence Test

For an infinite series \sum a_n, if \lim_{n \to \infty} a_n is anything but 0, the series diverges

Integral Test Conditions

1. Positive for all f(x) greater than 0 after x \geq 1

2. Continuous: Does not have jumps or discontinuities after x \geq 1

3. Decreasing: f’(x) \leq 0 for all x \geq 1

Direct Comparison Test for \sum a_n

1. Choose b_n that is less than a_n

2. If \sum_{n=1}^{\infty} b_n converges/diverges, a_n also converges/diverges respectivly

Limit Comparison Test for \sum a_n

1. Choose any b_n (does not need to be less than a_n)

   1. Ex: \frac{\sqrt{k}}{k+4} \approx \frac{k^{0.5}}{k} = k^{-0.5} so choose that as b_k

2. Find L=\lim_{n \rightarrow \infty} \frac{a_n}{b_n}

3. If 0 < L < \infty then \sum a_n or \sum b_n both will share the same behavior