17. Les méta-analyses

Méta-analyse

• Méthode statistique qui intègre les résultats de plusieurs études empiriques portant sur la même question de recherche

• Synthèse systématique et quantitative des résultats de recherche provenant de plusieurs études

• Permet d’obtenir une estimation groupée de l’ampleur de l’effet ou de résultat

• Permet de mieux estimer les effets sous-jacents sur la population que les études individuelles seules

• Comprendre une méta-analyse → interprétation pour les tailles d’effet

Avantages de la méta-analyse

• Plus qu’une seule étude

  • En combinant les données de plusieurs études, la méta-analyse augmente la précision de l’estimation de l’ampleur de l’effet

  • Permet de prendre en compte les résultats issus d’études avec des petites tailles d’échantillon → on va pouvoir augmenter la puissance

  • Améliorer l’applicabilité des résultats à des populations, des contextes et des lieux de recherche différents

• Aide à la résolution de conflit

  • Lorsque des études individuelle font état de résultats contradictoires, les méta-analyses aide à réconcilier ces divergences en analysant systématiquement les preuves collectives

  • Permettent d’identifier des tendances et des schémas généraux dans les études, ce qui permet de mieux comprendre la cohérence des résultats dans un domaine de recherche donné

Désavantages de la méta-analyse

• Que du publié

  • Les résultats statistiquement significatifs on 3x plus de chances d’être publiés que les résultats non significatifs → biais de publication

  • Les méta-analyses incluent des études dont l’ampleur de l’effet est plus importante → Sur-estimation de l’effet

    → peut-être pas aussi fort que la “réalité”

  • Pour chaque étude, les chercheurs peuvent aussi choisir de ne pas rapporter que certains résultats

• Hétérogénéité des études

  • Lorsque les études varient en termes de méthodologie, de populations étudiées ou de mesures utilisées, il devient difficile de comparer leurs résultats de manière cohérente

    → « comparer des pommes et des oranges »

  • Les effets observés peuvent différer selon des contextes spécifiques → réduit la précision des conclusions tirées, limiter la valeur scientifique

    de la méta-analyse.

  • Une sélection rigoureuse des études doit être réalisée pour garantir la validité dʼune méta-analyse

Biais de publication

Biais qui survient lorsque les résultats statistiquement significatifs ont plus de chances d'être publiés que les résultats non significatifs, conduisant à une surestimation de l'effet dans les méta-analyses.

Sur-estimation de l’effet

Une évaluation biaisée qui survient lorsque les méta-analyses incluent principalement des études avec des résultats significatifs, conduisant à des conclusions sur l'ampleur de l'effet qui sont plus élevées que la réalité.

Taille d'effet

• Mesure quantitative de l’ampleur d’un phénomène

  → association entre VI et VD

• Quantifie la force d’une relation entre des variables ou la taille de la différence entre des groupes

• Contrairement à la valeur p, qui indique seulement si un effet est statistiquement significatif, la taille d’effet quantifie son importance pratique

Pourquoi la taille d’effet est importante ?

• La taille d’effet permet l’interprétation des résultats d’une recherche

• Elle permet d’évaluer si un effet observé est suffisamment substantiel pour avoir une pertinence pratique ou clinique

→ Un résultat peut être statistiquement significatif mais n’avoir aucune utilité dans la pratique du psychologue

Indices les plus fréquents

• Le d de Cohen

• Le r² (Coefficient de détermination)

• Le Odd-Ratio (OR) (Rapport de cotes)

Le d de Cohen

• Mesure le degrés de séparation (en déviation standard) de deux distributions

• Différence (effet) pondérée par la déviation standard (permet de se “débarrasser de l’échelle”)

• Utilisé pour observer la différence entre un groupe expérimental et un groupe contrôle

→ Un d de Cohen de 0.5 indique que la moyenne d’un des groupes est situé à 0.5 déviation standard de l’autre

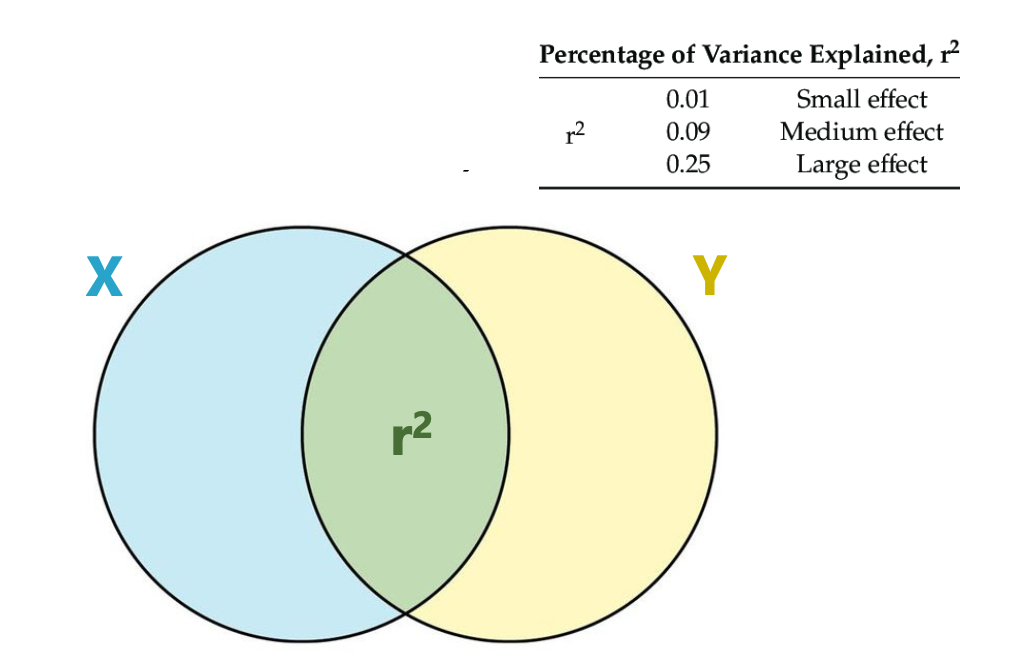
r² (coefficient de détermination)

• Mesure la proportion de la variance dans la variable dépendante qui est prévisible par (ou commune à) la variable indépendante

• Élévation au carré du coefficient de corrélation de Pearson (r)

• Utilisé pour évaluer la force d’une association entre deux variables quantitatives, ou la qualité de la prédiction d’un modèle de régression

→ Un r² de 0.5 indique que 50% de la variance de la variable dépendante est expliquée par / commune à la variable indépendante

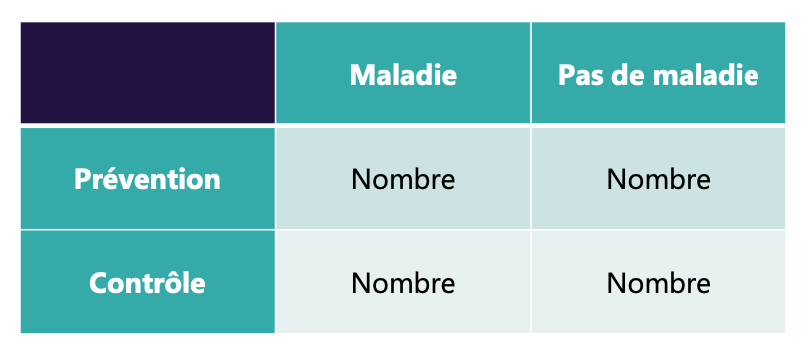
Odd-Ratio (OR) (Rapport de cotes)

• Les chances d’avoir une issue (outcome) plutôt qu’un autre, en sachant qu’on est dans un groupe donné (plutôt qu’un autre)

• Calculée en divisant les cotes de l’événement dans le groupe exposé par les cotes de l’événement dans le groupe non exposé

• En général utilisé dans des designs 2×2

→ Un OR de 2 indique que l’événement est deux fois plus probable dans le groupe exposé que dans le groupe non exposé

→ Un OR de 2 pour la prévention voudra dire que si vous êtes dans le groupe “prévention” , vous avez 2x moins de chance de tomber malade que dans le groupe contrôle → La prévention est innefficace

La taille d’effet dans les méta-analyses

• Les méta-analyses reposent sur l’intégration des tailles d’effets pour obtenir une vision globale et synthétique des résultats

• Utiliser les tailles d’effet (transformées) de chaque étude permet de les comparer, même si les études utilisent des mesures différentes

• Dans une méta-analyse, les tailles d’effet sont souvent pondérées (→ accorder plus ou moins d’importance) en fonction de la taille de l’échantillon ou de la précision des estimations (→ intervalles de confiance)

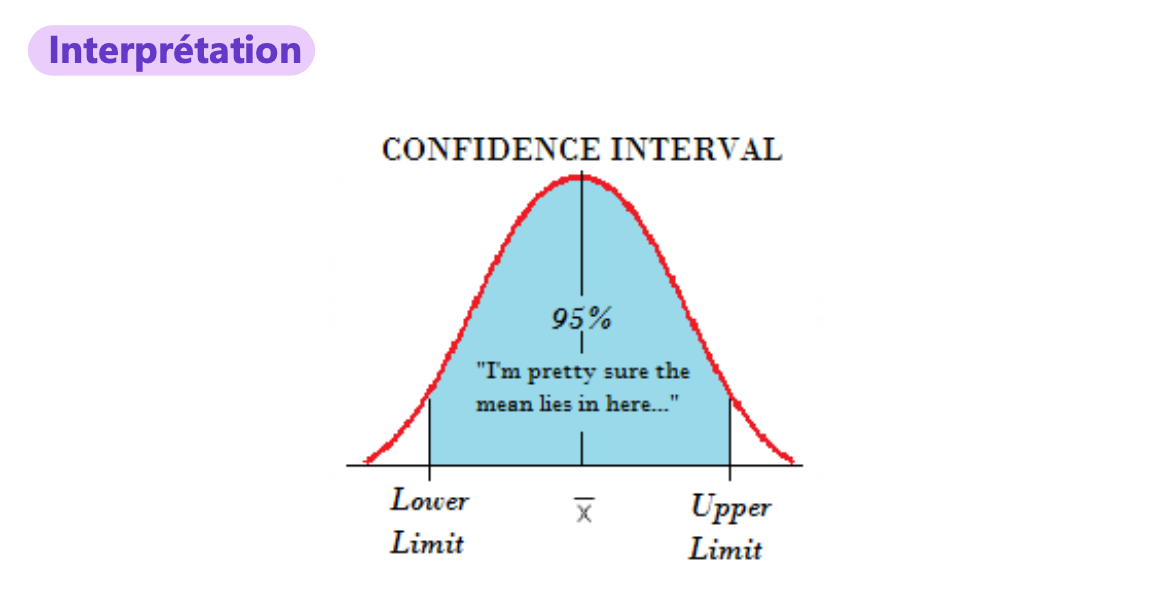
Intervalle de confiance

• L’intervalle de confiance d’un paramètre statistique (taille d’effet ou autre) est une plage de valeurs qui fournit une estimation plausible de la valeur réelle du paramètre dans la population étudiée

• Cette plage reflète le niveau de confiance qu’on a dans la valeur du paramètre (en général 95%)

  → quantifie l’incertitude associée à l’estimation

• Indique la précision des résultats

  → évite de se fier uniquement à une estimation ponctuelle

→ Un intervalle de confiance à 95% signifie que, si l’étude était répétée un grand nombre de fois, 95% des paramètres estimés seraient compris dans cet intervalle

Forest-plot

Graphique utilisé dans les méta-analyses pour visualiser les tailles d'effet individuelles des études, leurs intervalles de confiance, et l'effet combiné.

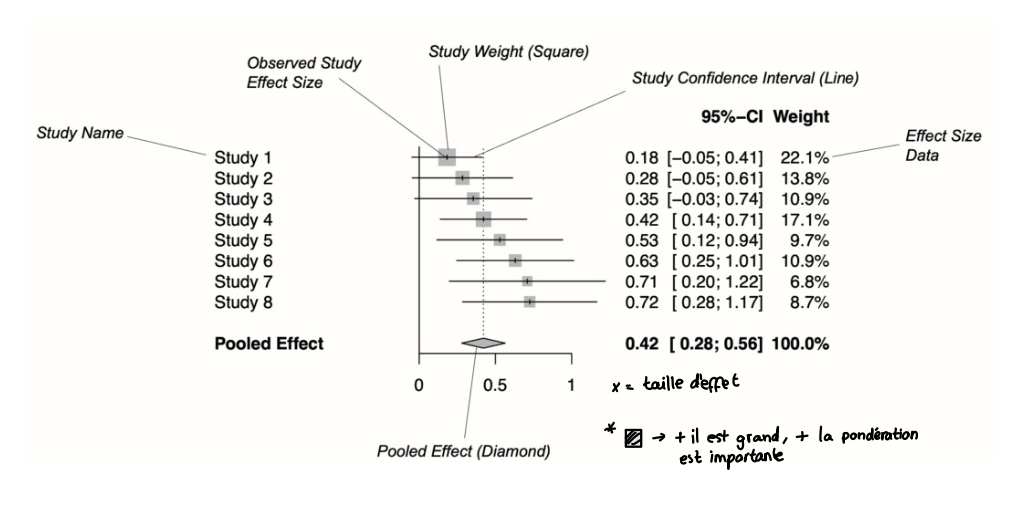
Pondération des études

• Dans une méta-analyse, les études sont pondérées en fonction de leur taille et de leur précision

• Plus de poids est donné aux études :

  • Avec de plus grands échantillons

  • Avec des intervalles de confiance plus restreints

• L’objectif est de donner une image plus précise et fiable de l’effet global en tenant compte de la qualité et de l’ampleur des études incluses

Effet combiné / Effet global

• On rassemble les tailles d'effet individuelles de chaque étude incluse dans la méta-analyse

• Chaque étude reçoit un poids basé sur sa précision. Les études avec des échantillons plus grands ou des estimations plus précises reçoivent des poids plus élevés

• On obtient une somme pondérée des tailles d'effet → taille d'effet combinée (sʼinterprète comme une taille dʼeffet et a son propre intervalle de confiance)

Étapes pour conduire une méta-analyse

1. Définir sa question de recherche

2. Faire une recherche systématique de toutes les études ayant testé cette question

3. Sélectionner les études selon les critères d’inclusion et d’exclusion

4. Extraire les tailles d’effet et les autres informations pertinentes

5. Rendre les tailles d’effet comparables entre elles et calculer le poids des études

6. Calculer l’effet combiné

1) Définir la question de recherche

1. Variables indépendantes et dépendantes

2. Effet modération / médiation

3. Population (Langue, Culture, Âge, Genre,…)

4. Types de plan de recherche

   → quelles mesures je veux prendre en compte

5. Période de publication (effet du temps, ou ancienne méta-analyses déjà disponibles)

3) Sélectionner les études : raisons pour l’exclusion

1. Question de recherche pas équivalente

   → (ou pas les bonnes VI / VD)

2. Base de données utilisées plusieurs fois

   → (trop de poids à une étude / un échantillon)

3. Pas une recherche avec des données réelles

   → (par ex. simulation)

   → toutes les données doivent être du même genre

4. Informations pertinentes non-disponibles

   → (par ex. taille dʼeffet)

5. Échantillon vraiment trop faible

   → (par ex. pour un sous-groupe)