Numbers - Factors + LCM

To write a number as a product of its prime factors

Find the smallest prime number that divides in (with no remainder) and divide.

1. Find the smallest prime number that divides into your answer and divide.

2. Repeat the process until your answer is 1.

3. Write your number as a product of all your prime divisors (on the left-hand side as in the examples below).

Example of how to write a number by the products of its prime factors.

Another q on to write. A number as a product of its prime number.

Note: ALL three q:s utilise the same method and way of doing things.

Determining How Many Factors a Number Has

For any natural number written in the form a, the number of factors will be one more than the power.

For any natural number whose prime factors are 𝑎 𝑥 × 𝑏 𝑦 the number of factors is found by adding one to each power and then multiplying these together.

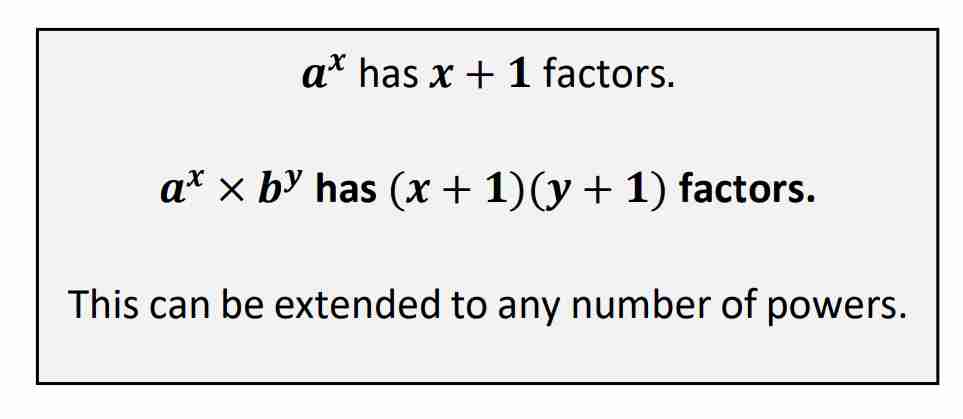
Single examples of finding how many factors a no. has…

A sample q on how it will be usually asked in the LC…

Determine how many factors 30 has and list those factors.

Remember this q has two parts:

(I) How many factors?

(ii) List all these factors.

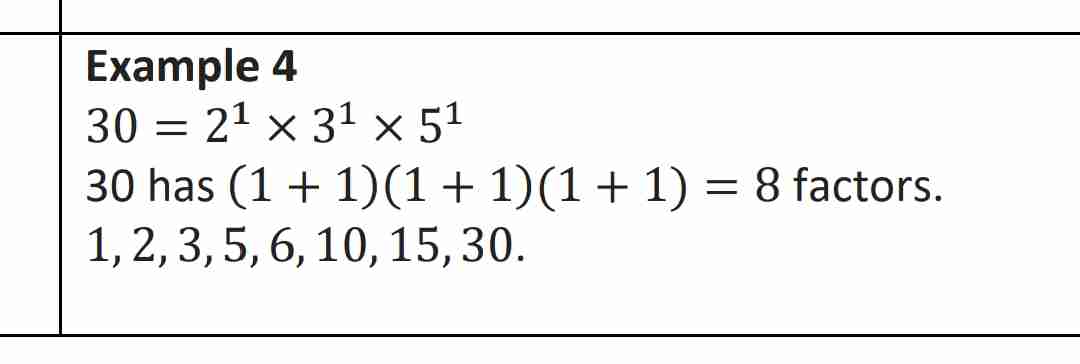
Even a two way table could be created for these q’s…

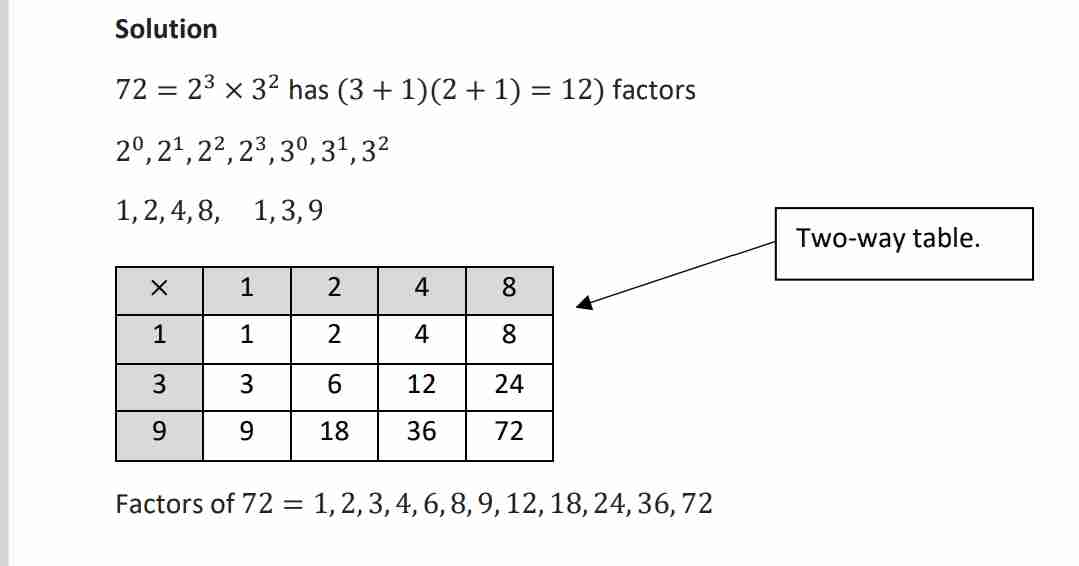
Q: Determine how many factors 72 has and list those factors.

The HCF can also be found by first expressing each number as a product of its prime factors.

Small numbers sample.

Q: 12, 18, 30.

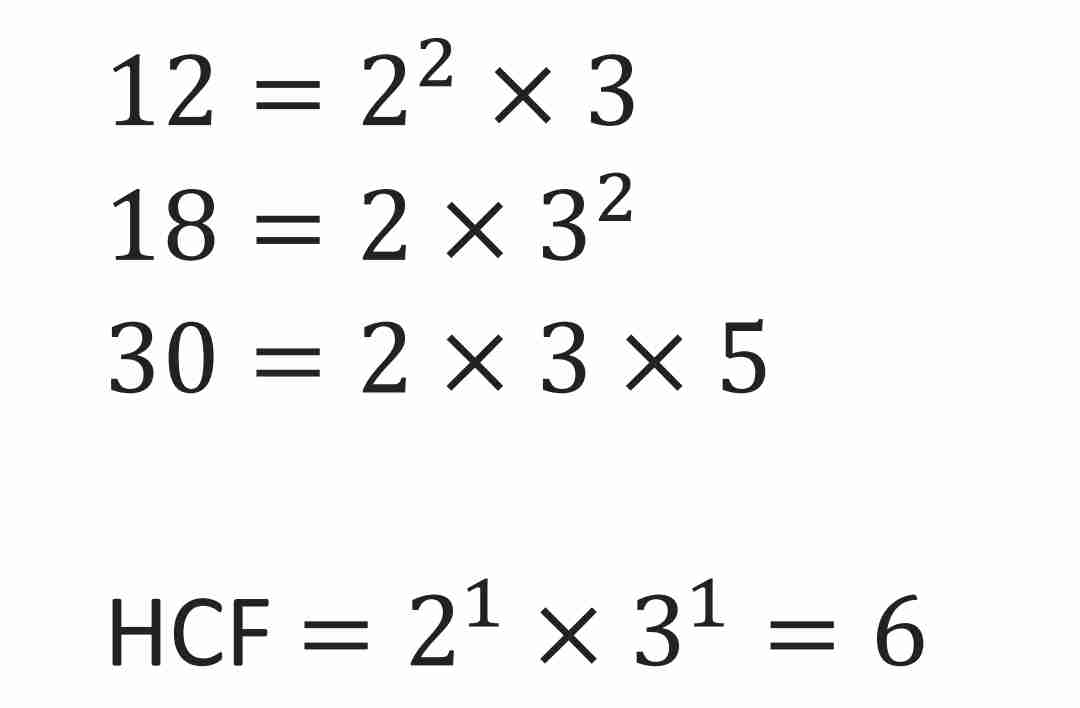
Big numbers sample.

Q: 432, 256.

What is LCM???

The LCM can also be found by first expressing each number as a product of its prime factors.

Example: Find the LCM LOWEST COMMON DENOMINATOR of these numbers…

3, 9, 12.

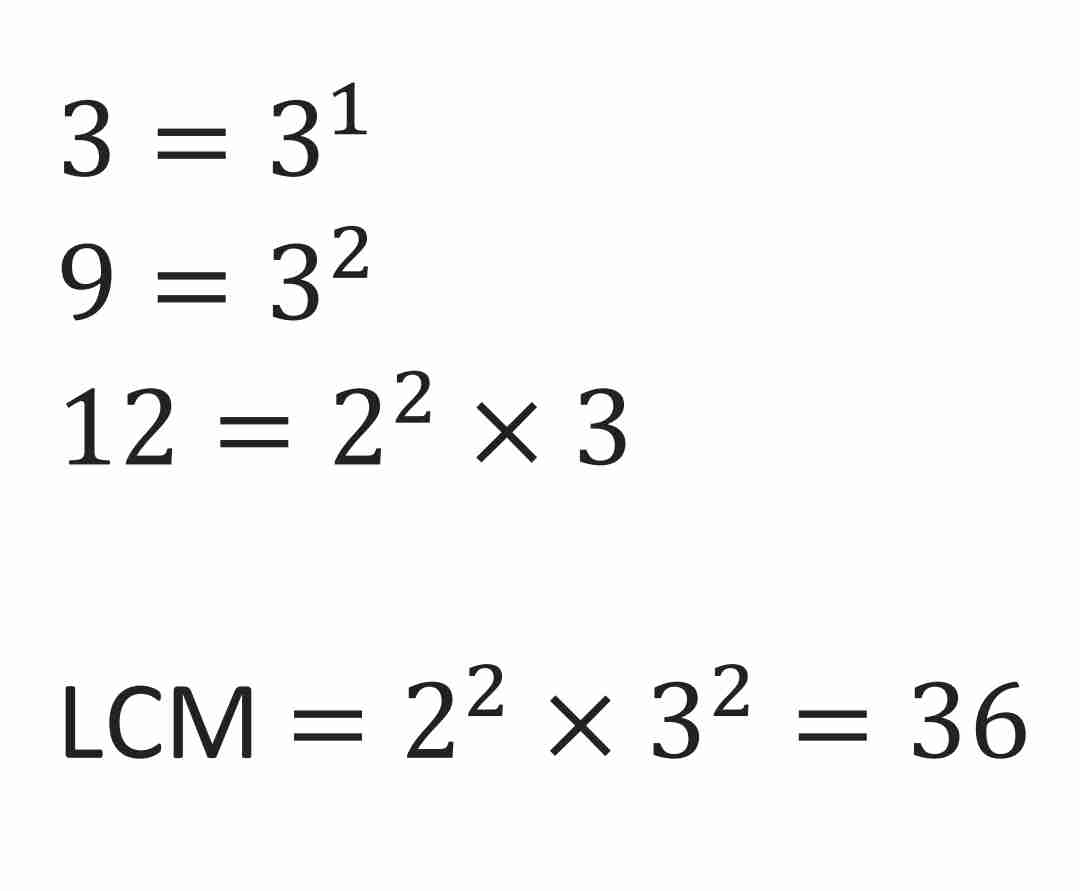
Larger numbers ex. Q ….

432, 256.

Division Method to find the HCF and LCM of TWO Natural Numbers:

Step 1: Write the largest number, divided by the smaller number as a fraction in its simplest form.

This step is a general rule for both.

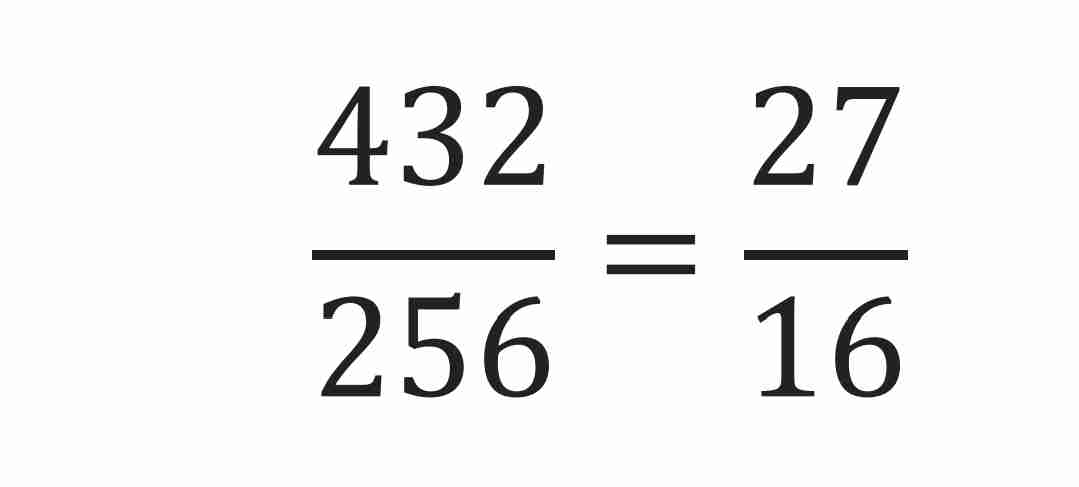
Division method to find HCF…

This method ONLY works for two natural numbers.

Division method to find LCM…

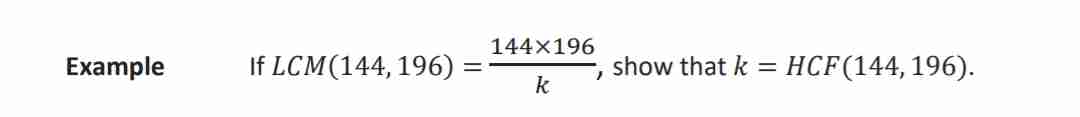
Very common sample LC Q:

To find k is easy as first you must find LCM of the pair of numbers and then in the question they say when you multiply that pair and divide it by k then it is equal to the LCM AND THEY say k is the HCF of the pair which is all enough to find the value of k and verify everything.