Chapter 4: A Gallery of Graphs

Flashcards covering key concepts from the lecture notes on graphing algebraic relations, including rectangular hyperbolas, truncus, square root functions and circles.

Practice Problem: Circles

The points (0,2) and (2,0) lie on the circumference of the circle with centre (−4, 0). Find the equation.

Let the center be (h, k) = (-4, 0). The radius r is the distance from the center to any point on the circle. Using the point (0, 2),
r = \sqrt{(-4 - 0)^2 + (0 - 2)^2} = \sqrt{16 + 4} = \sqrt{20}
The equation of the circle is
(x - h)^2 + (y - k)^2 = r^2
(x + 4)^2 + y^2 = 20

Practice Problem: Circles

The circle with equation (x – a)^2 + (y – b)^2 = 36 has its centre on the x-axis and passes through the point with coordinates (6, 6). What are the values of a and b?

Since the center is on the x-axis, b = 0. The equation becomes (x - a)^2 + y^2 = 36.
Given the point (6, 6):
(6 - a)^2 + 6^2 = 36
(6 - a)^2 = 0
a = 6
Thus, a = 6 and b = 0.

Practice Problem: Circles

Find the equation of a circle symmetrical to the y-axis that passes through the origin and (0, 4).

Since the circle is symmetrical to the y-axis and passes through the origin and (0, 4), the center must be at (0, 2) and the radius is 2.
(x - 0)^2 + (y - 2)^2 = 2^2
x^2 + (y - 2)^2 = 4

Practice Problem: Rectangular Hyperbola

Graph passes through the point (1,8). Find the value of 'a' in the rectangular hyperbola y = a/x + 3

Given y = a/x + 3 and the point (1, 8):
8 = a/1 + 3
a = 8 - 3 = 5
So, a = 5.

Practice Problem: Rectangular Hyperbola

Find the values of a, h, and k for the rectangular hyperbola y = a/(x-h) + k, given vertical asymptote x = 3, horizontal asymptote y = 4, and passing through the point (0, 6).

Given y = a/(x-h) + k, vertical asymptote x = 3, horizontal asymptote y = 4, and the point (0, 6):
From asymptotes: h = 3 and k = 4
So, y = a/(x - 3) + 4
Using the point (0, 6):
6 = a/(0 - 3) + 4
2 = a/(-3)
a = -6
Thus, a = -6, h = 3, and k = 4.

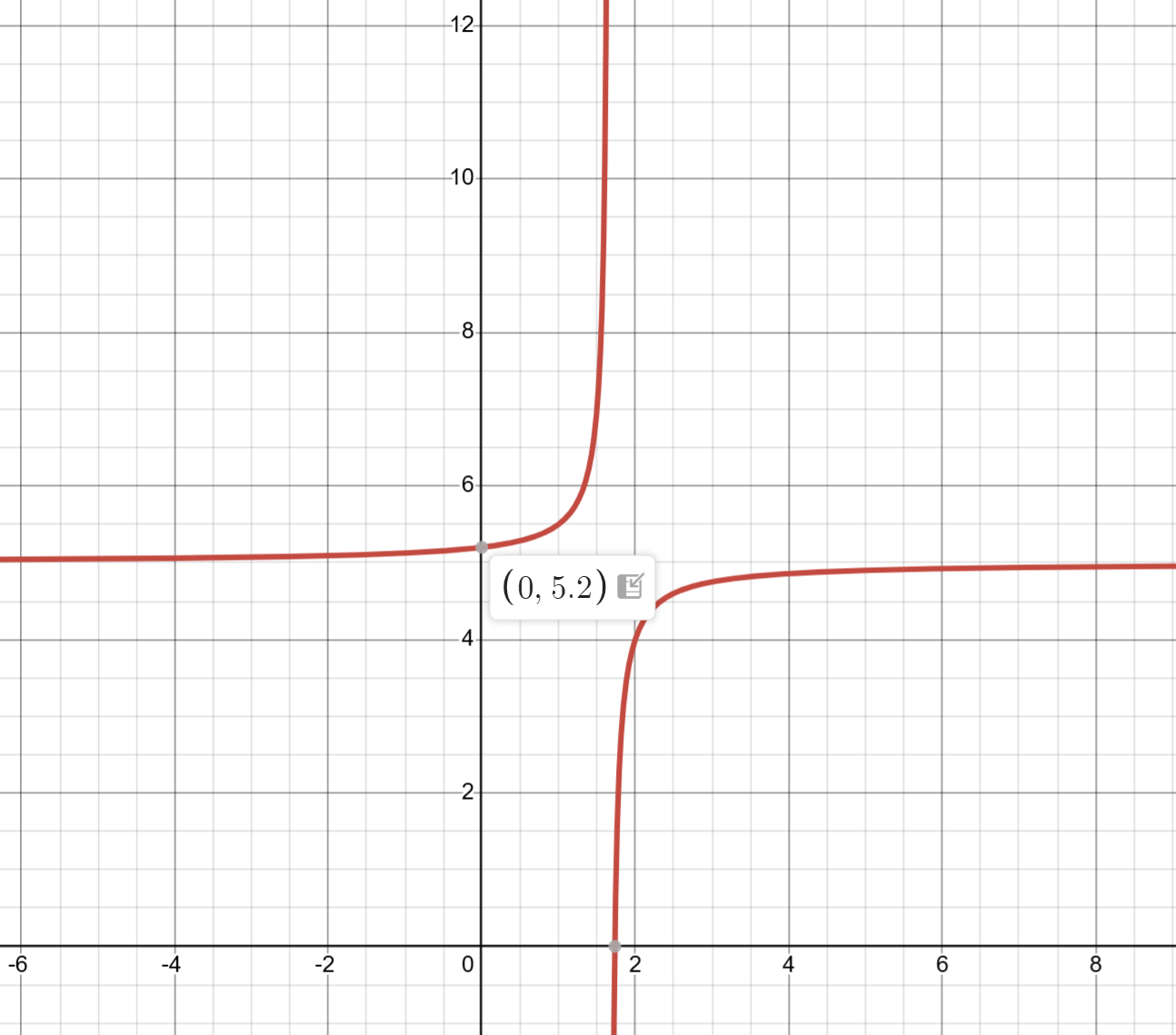
Practice Problem: Rectangular Hyperbola

Graph y = 5 −1/(3x − 5).

To graph y = 5 −1/(3x − 5), rewrite it as y = -1/(3(x - 5/3)) + 5.
Vertical asymptote: x = 5/3
Horizontal asymptote: y = 5
Plot additional points to sketch the graph.

Practice Problem: Square Root Function

Find the values of a and h for the equation y = a√x − h given the points (4,0) and (5, 1), where h<4.

Given y = a√x − h, and the points (4,0) and (5, 1):
Using (4, 0):
0 = a\sqrt{4 - h}
Since a cannot be zero, h = 4.
But given h < 4, there may be an error in the problem statement. Assuming h = 4, using the point (5, 1) is not possible with the condition h<4.
If we ignore the constraint that h<4, then:
1 = a\sqrt{5 - 4}
a = 1
Thus, a = 1 and h = 4.

Practice Problem: Square Root Function

If y = a√x − h + k passes through the point (5,4), what are some possible values of a, h, and k?

Given y = a√x − h + k passes through (5,4), we have 4 = a\sqrt{5 - h} + k.
Let's choose some values:
If h = 5, then 4 = a\sqrt{0} + k, so k = 4. Then a can be any value.
If a = 1, then 4 = \sqrt{5 - h} + k. If k = 3, then 1 = \sqrt{5 - h}, so h = 4.
Thus, one possible set of values is a = 1, h = 4, and k = 3.

Practice Problem: Semicircle

Determine the equation for a semicircle with a radius of 3, and center on the y-axis at (0,3) using a negative square root.

Semicircle with radius 3, center at (0,3) using a negative square root:
(x - 0)^2 + (y - 3)^2 = 3^2
x^2 + (y - 3)^2 = 9
(y - 3)^2 = 9 - x^2
y - 3 = -\sqrt{9 - x^2}
y = 3 - \sqrt{9 - x^2}

What type of transformation is this?

Describe the transformation applied to the graph of y=2/x to obtain the graph of y=2/(x+1) - 3

The graph of y = 2/x is transformed to y = 2/(x+1) - 3.
This involves a horizontal translation 1 unit to the left and a vertical translation 3 units down.

Question: Asymptotes

What are the asymptotes of y = 1/x^2?

For y = 1/x^2, the asymptotes are:
Vertical asymptote: x = 0
Horizontal asymptote: y = 0

Question: Transformation

Describe the transformation applied to the graph of y = −1/2x^2 to obtain the graph of y = −1/(2(x + 3)^2) − 4

The graph of y = −1/2x^2 is transformed to y = −1/(2(x + 3)^2) − 4.
This involves a horizontal translation 3 units to the left and a vertical translation 4 units down.

Question: Domain and Range

Determine the domain and range of y = 3√x+1 − 6

For y = 3√x+1 − 6,
Domain: x ≥ -1 or [-1, \infty)
Range: y ≥ -6 or [-6, \infty)

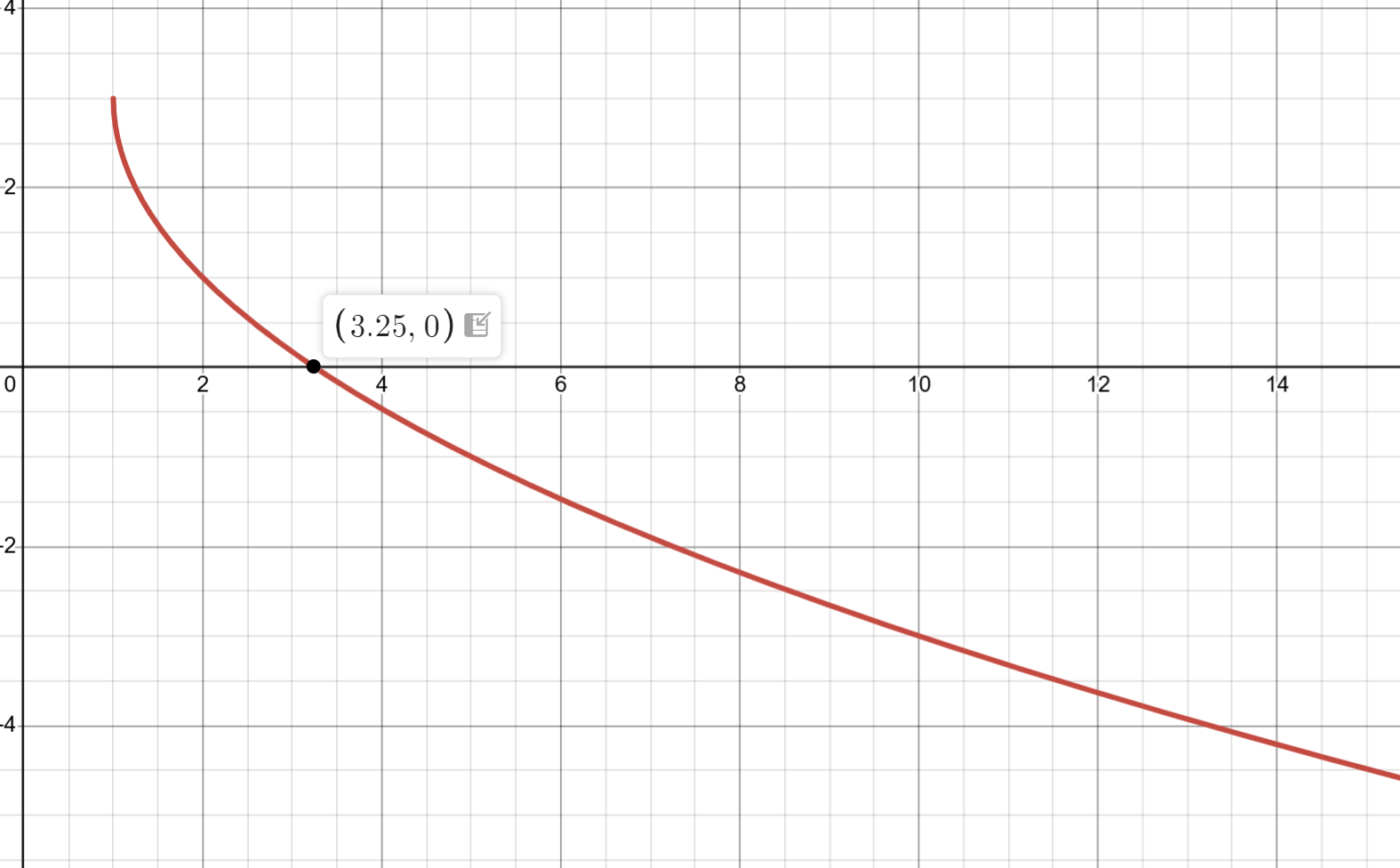
Question: Graph

Describe the graph of y = −2√x − 1 + 3

For y = −2√x − 1 + 3,
The graph is a square root function reflected over the x-axis, stretched vertically by a factor of 2, shifted 1 unit to the right, and shifted 3 units up.

Question: Key Features

What are the key features of y = −2√x − 1 + 3?

For y = −2√x − 1 + 3,
Domain: x ≥ 1 or [1, \infty)
Range: y ≤ 3 or (-\infty, 3]
x-intercept: Set y = 0 and solve for x.
y-intercept: There is no y-intercept.

Question: Domain and Range

What is the domain and range of y = √2 − x + 3?

For y = √2 − x + 3,
Domain: x ≤ 2 or (-\infty, 2]
Range: y ≥ 3 or [3, \infty)

Question: Circle Equation

What is the equation for a circle with center (h, k) and radius r?

The equation for a circle with center (h, k) and radius r is:
(x - h)^2 + (y - k)^2 = r^2

Question: Circle Description

Describe the circle represented by the equation (x − 1)^2 + (y − 2)^2 = 4

The circle (x − 1)^2 + (y − 2)^2 = 4 has:
Center: (1, 2)
Radius: r = \sqrt{4} = 2
It is a circle centered at (1, 2) with a radius of 2.

Question: Circle Features

What are the key features of (x + 1)^2 + (y + 4)^2 = 9?

The circle (x + 1)^2 + (y + 4)^2 = 9 has:
Center: (-1, -4)
Radius: r = \sqrt{9} = 3

Question: Sketching Circles

How can you sketch a circle with an equation in the general form?

To sketch a circle with an equation in the general form:

1. Rewrite the equation in the standard form (x - h)^2 + (y - k)^2 = r^2.
2. Identify the center (h, k) and radius r.
3. Plot the center and draw the circle using the radius.

Question: Semicircle Transformation

Describe the graph of y = −2 + √(49 − (x − 2)^2).

The graph of y = −2 + √(49 − (x − 2)^2) is a semicircle.
Rewrite it as y = -2 + \sqrt{49 - (x - 2)^2}.
This is a semicircle centered at (2, -2) with a radius of 7, lying above y = -2.

Practice Problem: Circles

State the coordinates for center point and length of radius for the following circle: (x-2)^2+(y+5)^2 = 16

Given equation: (x-2)^2+(y+5)^2 = 16
Center point: (2, -5)
Length of radius: √16 = 4

Practice Problem: Square Root Function

What is the domain for the following square root function: y = 3\sqrt{x-6}+4

The expression inside the square root must be greater than or equal to zero.
x - 6 ≥ 0
x ≥ 6
Therefore, the domain is x ≥ 6.

Domain: [6, ∞)

Practice Problem: Combining radicals

Solve for x: \sqrt{5x-1} = \sqrt{3x+4}

To solve the equation \sqrt{5x-1} = \sqrt{3x+4}, square both sides:
5x - 1 = 3x + 4
2x = 5
x = \frac{5}{2}
Check: \sqrt{5(\frac{5}{2})-1} = \sqrt{\frac{25}{2}-\frac{2}{2}} = \sqrt{\frac{23}{2}}
\sqrt{3(\frac{5}{2})+4} = \sqrt{\frac{15}{2}+\frac{8}{2}} = \sqrt{\frac{23}{2}}

Practice Problem: Rectangular Hyperbola

What is the horizontal asympotote of: y=\frac{1}{x+5}-3

For the rectangular hyperbola y = \frac{1}{x+5} - 3, the horizontal asymptote is the value that y approaches as x goes to infinity or negative infinity.
y = -3

Practice Problem: Linear Equation

Solve for x: \frac{1}{3} = \frac{1}{x-5}.

To solve for x in the given equation:
\frac{1}{3} = \frac{1}{x-5}
Cross-multiply:
x - 5 = 3
x = 3 + 5
x = 8

Practice Problem: Quadratic Equation

Write the quadratic equation for the following roots: -5 and 7

Given roots -5 and 7, the quadratic equation can be written as:
(x + 5)(x - 7) = 0
Expanding this gives:
x^2 - 7x + 5x - 35 = 0
x^2 - 2x - 35 = 0

Practice Problem: Combining Radicals

What is the simplified form of 3\sqrt{5} + 4\sqrt{5}

To simplify the expression:
3\sqrt{5} + 4\sqrt{5}
Since the radicals are the same, you can combine like terms:
(3 + 4)\sqrt{5}
7\sqrt{5}

Practice Problem: Quadratic Equation

Factor the following quadratic equation: x^2+5x+6

To factor the quadratic equation x^2 + 5x + 6, look for two numbers that multiply to 6 and add to 5. These numbers are 2 and 3.
(x + 2)(x + 3)

Question: Linear Equations

Is y=3x+6 a linear function?

Yes, y = 3x + 6 is a linear function because it is in the form y = mx + b, where m and b are constants.

Practice Problem: Square Root Functions

Find the equation of a square root function that shifts the graph 4 units to the left and 2 units down.

To shift the graph 4 units to the left and 2 units down, the transformation is:
y = \sqrt{x + 4} - 2
So the equation is y = \sqrt{x + 4} - 2.

Practice Problem: Circles

Find the equation of a circle which is reflected across the y-axis.

Reflecting a circle across the y-axis does not change its equation if the center is on the y-axis. If the original circle is (x-h)^2 + (y-k)^2 = r^2, the reflected circle is (-x-h)^2 + (y-k)^2 = r^2 or (x+h)^2 + (y-k)^2 = r^2.
If you have a circle centered at (a,b) with radius r, the reflected equation would be (x+a)^2 + (y-b)^2 = r^2

Practice Problem: Semi-Circles

Provide an example of an equation can be used to generate a semi-circle using a positive square root with a radius of 5 and a center at (0,0).

A semi-circle using a positive square root with a radius of 5 and a center at (0,0) can be represented by:
y = \sqrt{25 - x^2}

Practice Problem: Rectangular Hyperbola

Find the equation of the rectangular hyperbola if the vertical asymptote is at x=2 and the horizontal asymptote at y=-1.

If the vertical asymptote is at x=2 and the horizontal asymptote is at y=-1, the rectangular hyperbola can be represented as:
y = \frac{a}{x - 2} - 1
Assuming a=1, the equation is:
y = \frac{1}{x - 2} - 1

Concept Check: Linear Equations

True or False: The equation y=4 is a linear equation

True. The equation y=4 is a linear equation because it can be written in the form y = mx + b, where m=0 and b=4.

Practice Problem: Quadratic Equation

What is the graph for the equation: \frac{1}{2}(x+2)^2-3

For the equation \frac{1}{2}(x+2)^2 - 3:
It's a parabola that opens upwards.
Vertex: (-2, -3)
It is vertically compressed by a factor of 1/2.

Practice Problem: Circles

If a circle's diameter is 10 units and its center is at (3,4), what is the equation of this circle?

If the diameter is 10 units, the radius is 5 units. The center is at (3,4), so the equation of the circle is:
(x - 3)^2 + (y - 4)^2 = 25

Practice Problem: Square Root Function

Determine the range: y = −5√(x + 2) − 1

For the function y = −5√(x + 2) − 1:
Since the square root function is always non-negative, √x ≥ 0.
−5√x ≤ 0
−5√(x + 2) − 1 ≤ −1
Thus, the range is y ≤ −1.

Range: (−∞, −1]

Practice Problem: Square Root Function

Describe the transformations if the original square root function is y = √x: y = −√(-x) + 3

Given y = √x:
y = −√(-x) + 3 is a reflection across the y-axis, a reflection across the x-axis, and a vertical shift up by 3 units.

Practice Problem: Basic Radical Equations

Solve for x: √x + 1 = 5

To solve for x in the equation √x + 1 = 5:
√x = 5 - 1
√x = 4
Square both sides: x = 16

Practice Problem: Rectangular Hyperbola

For the equation y = 3/(x - 2) + 1,