matrix-vector multiplication

for every point p (a1, a2, …, an) there is a corresponding vector

(0,0,…,0) to p, denoted (see image)

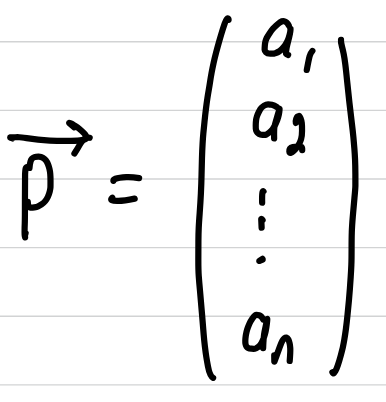
zero vector facts

for all A m x n, A0→ = 0v1 + 0v2 + … + 0vn = 0→

for all v ∈ Rⁿ, v + 0→ = v

dot product

Let v and u be column vectors

their dot product is the scalar v·u = a1b1 + a2b2 + … + anbn

properties of matrix vector multiplication

A(x + y) = Ax + Ay

A(cx) = c(Ax) = (cA)x

(A + B)x = Ax + Bx

standard basis vectors e1, e2, en

e1 = column of 1, 0, 0…, 0

e2 = column of 0, 1, 0, …, 0

en = column of 0, 0, 0…, 1

Aei =

vi (only picks up one column)

identity matrix

the matrix with columns e1, e2, …, en

for every v ∈ Rⁿ, I_nv =

v

any linear combination of solutions to _ system is also a _

homogeneous, solution

associated homogenous system

for system Ax→ = b→, the system Ax→ = 0→ is called the associated homogeneous system