Derivatives and Anti-Derivatives
1/63
Earn XP
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
64 Terms
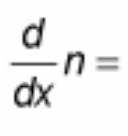
(d/dx) n = ?
? = 0
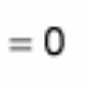
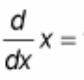
(d/dx) x = ?
? = 1
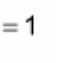
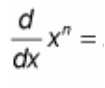
(d/dx) x^(n) = ?
? = nx^(n - 1)
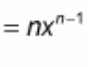
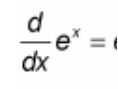
(d/dx) e^(x) = ?
? = e^x
Since the slope is the same as the function at every point on the graph, then the derivative of this function will be itself, as the derivative gives you the slope of the function
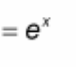
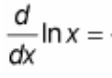
(d/dx) ln(x) = ?
? = 1 / x
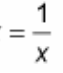
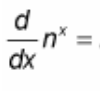
(d/dx) n^(x) = ?
FIXED: ? = [n^(x)] * [ln(n)]
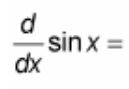
(d/dx) sin(x) = ?
? = cos(x)
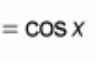
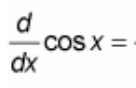
(d/dx) cos(x) = ?
? = - sin(x)
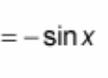
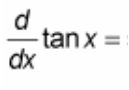
(d/dx) tan(x) = ?
? = sec²(x)
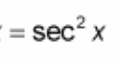
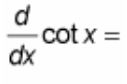
(d/dx) cot(x) = ?
? = - csc²(x)
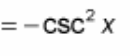
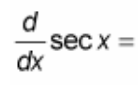
(d/dx) sec(x) = ?
? = sec(x)tan(x)
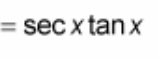
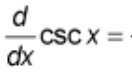
(d/dx) csc(x) = ?
? = - csc(x)cot(x)
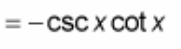
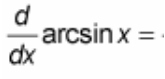
(d/dx) arcsin(x) = ?
? = 1 / √(1 - x²)
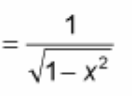
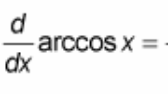
(d/dx) arccos(x) = ?
? = -1 / √(1 - x²)
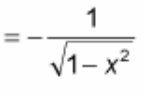

(d/dx) arctan(x) = ?
? = 1/(1 + x²)
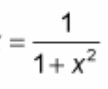

(d/dx) arccot(x) = ?
? = -1 / (1 + x²)
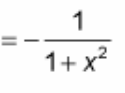

(d/dx) arcsec(x) = ?
? = 1 / [x√(x² - 1)]
![<p>? = 1 / [x√(x² - 1)]</p>](https://knowt-user-attachments.s3.amazonaws.com/d7de60e6-2027-4a6d-810b-760debc11e11.jpeg)
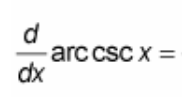
(d/dx) arccsc(x) = ?
? = -1 / [x√(x² - 1)]
![<p>? = -1 / [x√(x² - 1)]</p>](https://knowt-user-attachments.s3.amazonaws.com/4dd0776c-b005-44ad-9f63-f5d92e932d1d.jpeg)
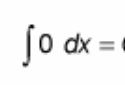
∫ 0 dx = ?
? = C
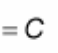
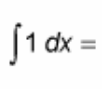
∫ 1 dx = ?
? = x + C
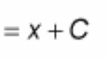
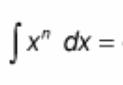
∫ x^(n) dx = ?
? = {[x^(n+1)] / [n + 1]} + C
![<p>? = {[x^(n+1)] / [n + 1]} + C</p>](https://knowt-user-attachments.s3.amazonaws.com/a77ae5eb-8048-413c-b5a2-6437a22a818e.jpeg)
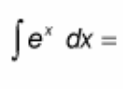
∫ e^(x) dx = ?
? = e^(x) + C
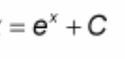
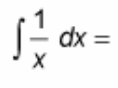
∫ (1 / x) dx = ?
? = ln|x| + C
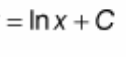
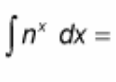
∫ n^(x) dx = ?
? = [n^(x) / ln(n)] + C
![<p>? = [n^(x) / ln(n)] + C</p>](https://knowt-user-attachments.s3.amazonaws.com/c6f78c7b-7621-4fc5-a859-d86ef10f7f66.jpeg)
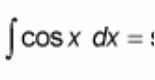
∫ cos(x) dx = ?
? = sin(x) + C
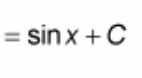
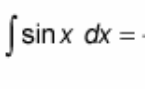
∫ sin(x) dx = ?
? = - cos(x) + C
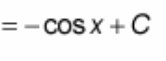
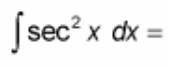
∫ sec²(x) dx = ?
? = tan(x) + C
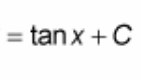
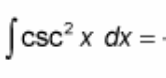
∫ csc²(x) dx = ?
? = - cot(x) + C
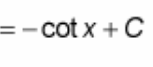
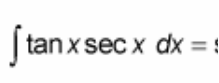
∫ tan(x)sec(x) dx = ?
? = sec(x) + C
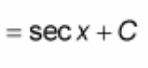
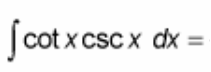
∫ cot(x)csc(x) dx = ?
? = - csc(x) + C
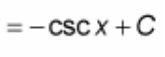
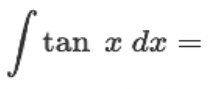
∫ tan(x) dx = ?
? = ln |sec(x)| + C
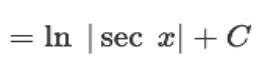
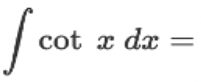
∫ cot(x) dx = ?
? = ln |sin(x)| + C
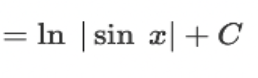
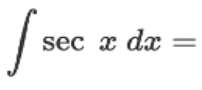
∫ sec(x) dx = ?
? = ln |sec(x) + tan(x)| +C
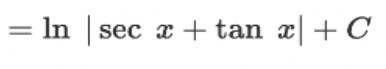
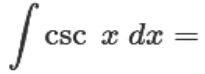
∫ csc(x) dx = ?
? = -ln |csc(x) + cot(x)| +C
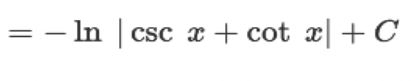
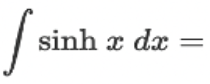
∫ sinh(x) dx = ?
? = cosh(x) + C
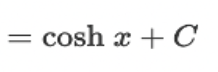
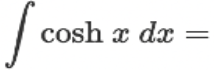
∫ cosh(x) dx = ?
? = sinh(x) + C
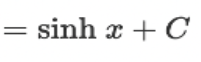
![<p>∫ [dx / √(a² - x²)] = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/e3bc9365-0806-4498-b894-3c06712f9553.jpeg)
∫ [dx / √(a² - x²)] = ?
? = sin^(-1)(x / a) + C
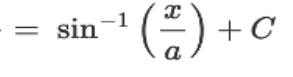
![<p>∫ [dx / (a² + x²)] = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/53486ce2-0f76-4431-b806-47c935d54da6.jpeg)
∫ [dx / (a² + x²)] = ?
? = (1 / a) * tan^(-1)(x / a) + C
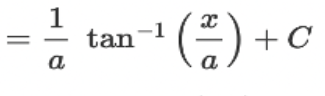
![<p>∫ [dx / x√(x² - a²)] = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/f64b9325-5fe5-4fc5-89a3-bd3b57c85275.jpeg)
∫ [dx / x√(x² - a²)] = ?
? = (1 / a) * sec^(-1)|x / a| + C
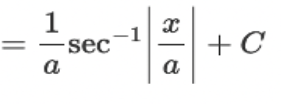
![<p>∫ [dx / √(a² + x²)] = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/cd9bf0b5-253b-44bd-84ae-91709dc73876.jpeg)
∫ [dx / √(a² + x²)] = ?
? = sinh^(-1)(x / a) + C
so long as a > 0
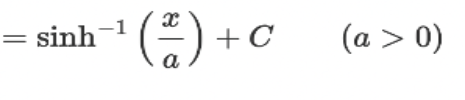
![<p>∫ [dx / √(x² - a²)] = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/396d7bc3-7f81-4fbb-998e-bb44bf30cd63.jpeg)
∫ [dx / √(x² - a²)] = ?
? = cosh^(-1)(x / a) + C
so long as x > a > 0
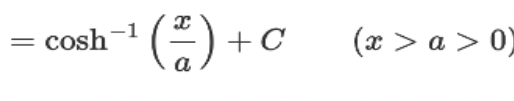
![<p>∫ [1 / √(1-x²)] dx = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/838d2743-993d-4ca1-98dc-45316e63bed3.jpeg)
∫ [1 / √(1-x²)] dx = ?
? = arcsin(x) + C
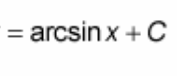
![<p>∫ [-1 / √(1-x²)] dx = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/2af10a34-344e-4bb2-ae8b-69cfa45a717b.jpeg)
∫ [-1 / √(1-x²)] dx = ?
? = arccos(x) + C
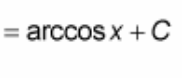
![<p>∫ [1 / (1 + x²)] dx = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/31442c05-b0c3-4d7c-b42b-485aa5853dd8.jpeg)
∫ [1 / (1 + x²)] dx = ?
? = arctan + C
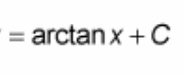
![<p>∫ [-1 / (1 + x²)] dx = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/e1cdcf8a-9f5d-43ad-87be-62bfc32c12f5.jpeg)
∫ [-1 / (1 + x²)] dx = ?
? = arccot(x) + C
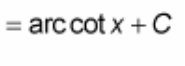
![<p>∫ 1 / [x√(x² - 1)] dx = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/2a71e488-2cae-4b65-9b8d-f2c325516cf5.jpeg)
∫ 1 / [x√(x² - 1)] dx = ?
? = arcsec(x) + C
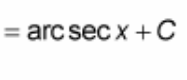
![<p>∫ -1 / [x√(x² - 1)] dx = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/09824f82-868a-4fbb-92ed-44b5c8dcd950.jpeg)
∫ -1 / [x√(x² - 1)] dx = ?
? = arccsc(x) + C
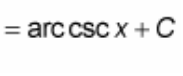
Derivative Power Rule
The power rule states that if n is any real number, then the derivative is:
Derivative Sum and Difference Rule
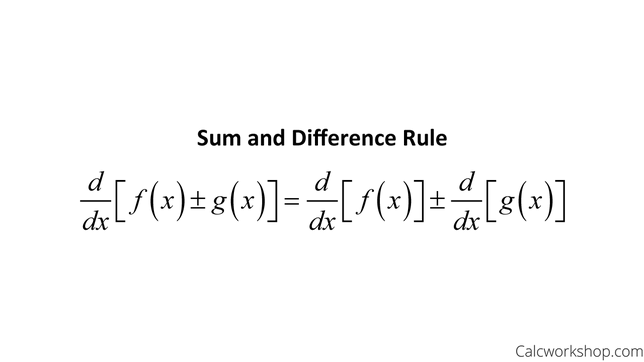
Derivative Constant Multiple Rule
The constant multiple rule states that if c is a constant and f(x) is a differentiable function, then:
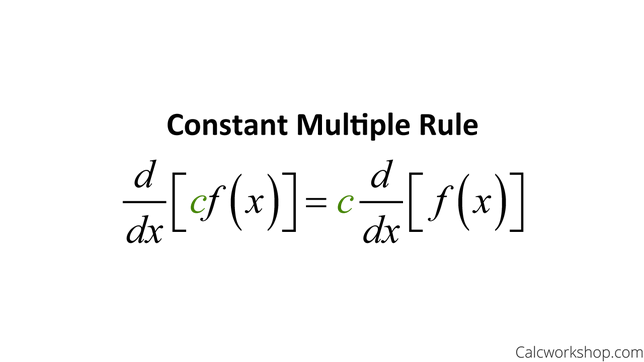
Derivative Product Rule
The product rule states that if f(x) and g(x) are both differentiable functions, then the derivative of their product also exists.
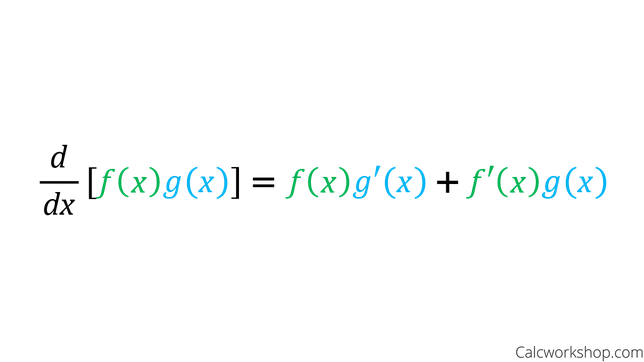
Derivative Quotient Rule
The quotient rule states that if f(x) and g(x) are both differentiable functions and g(x) does
not equal zero, then the derivative of their quotient also exists.
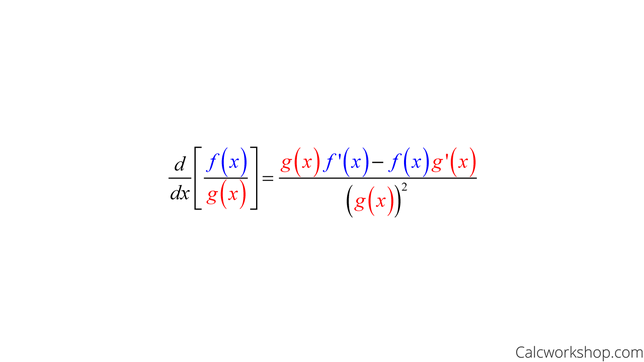
Derivative Chain Rule
The chain rule states that if f(x) and g(x) are both differentiable functions and the composite function defined as F=f(g(x)), then F is differentiable, and F’ is given by the product.
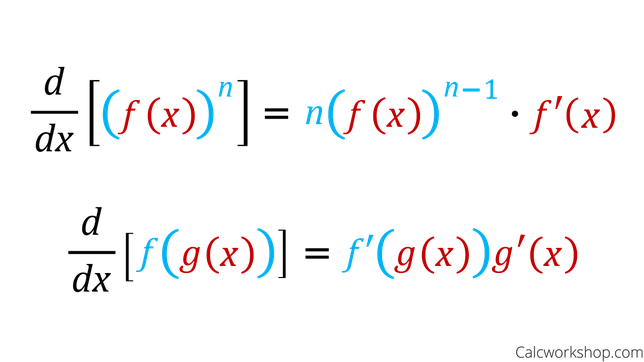
Anti-Derivative Power Rule
Now, the antiderivative rule of power of x is given by ∫xn dx = xn+1/(n + 1) + C, where n ≠ -1. Using the antiderivative power rule, we can conclude that for n = 0, we have ∫x0 dx = ∫1 dx = ∫dx = x0+1/(0+1) + C = x + C. Please do not confuse this power antiderivative rule ∫xn dx = xn+1/(n + 1) + C, where n ≠ -1 with the power rule of derivatives which is d(xn)/dx = nxn-1.
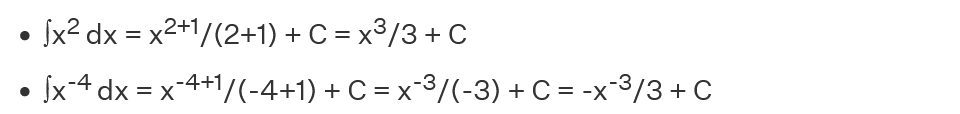
Anti-Derivative Chain Rule
The chain rule of derivatives gives us the antiderivative chain rule which is also known as the u-substitution method of antidifferentiation. The antiderivative chain rule is used if the integral is of the form ∫u'(x) f(u(x)) dx.
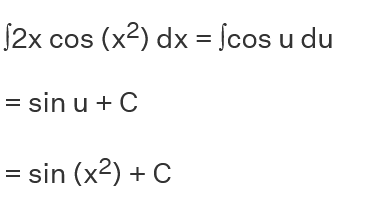
Steps to Integration by U-Substitution
Step - 1: Choose a new variable u for the given function to be reduced.
Step - 2: Determine the value of dx, of the given integral, where f(x) is integrated with respect to x.
Step - 3: Make the required substitution in the function f(x), and the new value dx.
Step - 4: Integrate the function obtained after substitution
Step - 5: Substitute back the initial variable x to obtain the final answer.
Anti-Derivative Product Rule
aka Integration by Parts Rule
The formula for the antiderivative product rule is:
∫ U dv = UV - ∫ V du.
or
∫ (first function) (second function) dx = first function ∫ (second function) dx - ∫ [ d/dx (first function) ∫ (second function dx) ] dx
Usually, the first function (u) will be selected in such a manner that the process of finding the integral of its derivative must be easy. To simplify the selection of the first function, we use the ILATE rule.
Letters of I.L.A.T.E. Rule
(I)nverse Trigonometric Functions
(L)ogarithmic Functions
(A)lgebraic Functions
(T)rigonometric Functions
(E)xponential functions
Remember the order of importance is [ IL ] A [ TE ], where the first two and last two are of equal importance
![<ul><li><p>(I)nverse Trigonometric Functions</p></li><li><p>(L)ogarithmic Functions</p></li><li><p>(A)lgebraic Functions</p></li><li><p>(T)rigonometric Functions</p></li><li><p>(E)xponential functions</p></li></ul><p>Remember the order of importance is [ IL ] A [ TE ], where the first two and last two are of equal importance</p>](https://knowt-user-attachments.s3.amazonaws.com/a18c3a06-14a6-4a69-8bf0-d63d9ccfe502.jpeg)
Steps of applying I.L.A.T.E. Rule
Identify the type of each function as Inverse trigonometric (I), Logarithmic (L), Algebraic (I), Trigonometric (T), or Exponential (E).
See which of the given functions comes first in the order of ILATE (or) LIATE and choose it as the first function.
Select the remaining function as the second function.
Then apply the integration by parts formula.

![<h2 collapsed="false">Integral Properties: Sum/Difference </h2><p>a∫b [f(x) ± g(x)] dx = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/84b1e284-1eb8-4fec-aefa-93015b9583eb.jpeg)
Integral Properties: Sum/Difference
a∫b [f(x) ± g(x)] dx = ?
? = a∫b [f(x)] dx ± a∫b [g(x)] dx
![<p>? = a∫b [f(x)] dx ± a∫b [g(x)] dx</p>](https://knowt-user-attachments.s3.amazonaws.com/f01b6f2c-9b2e-45d5-9c9e-dce90fa627c5.jpeg)
![<h2 collapsed="false">Integral Properties: Constant Multiple </h2><p>a∫b [k * f(x)] dx = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/87ef0669-77e4-4ea7-9ed5-f591dc661be8.jpeg)
Integral Properties: Constant Multiple
a∫b [k * f(x)] dx = ?
? = k * [a∫b [f(x) dx]
![<p>? = k * [a∫b [f(x) dx]</p>](https://knowt-user-attachments.s3.amazonaws.com/f635a7cd-b646-4921-8d0b-cf9a2fc9d51e.jpeg)
![<h2 collapsed="false">Integral Properties: Reverse Interval </h2><p>a∫b [f(x)] dx = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/d03364a8-f975-4d49-9e97-dd449681c4a2.jpeg)
Integral Properties: Reverse Interval
a∫b [f(x)] dx = ?
? = - [b∫a [f(x) dx]
![<p>? = - [b∫a [f(x) dx]</p>](https://knowt-user-attachments.s3.amazonaws.com/10c2ffc8-eb14-44be-a5bb-46df4c30db45.jpeg)
![<h2 collapsed="false">Integral Properties: Zero-Length Interval </h2><p>a∫a [f(x)] dx = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/e7e7ad05-f5fa-44e3-b682-821b043dae64.jpeg)
Integral Properties: Zero-Length Interval
a∫a [f(x)] dx = ?
? = 0
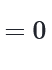
![<h2 collapsed="false">Integral Properties: Adding/Combining Intervals</h2><p>a∫b [f(x)] dx + b∫c [f(x)] dx = ?</p>](https://knowt-user-attachments.s3.amazonaws.com/c6d45a62-1023-4970-9935-becfaaa45719.jpeg)
Integral Properties: Adding/Combining Intervals
a∫b [f(x)] dx + b∫c [f(x)] dx = ?
? = a∫c [f(x)] dx
![<p>? = a∫c [f(x)] dx </p>](https://knowt-user-attachments.s3.amazonaws.com/8435ef10-196b-4773-9524-4409826247f9.jpeg)