MATH 223 Final

Vector Space Axiom 1

Commutativity: u+w=w+u

Vector Space Axiom 2

Associativity: (u+v)+w=u+(v+w)

Vector Space Axiom 3

Zero Vector: satisfies u+0=u

Vector Space Axiom 4

Additive Inverse: for all vectors in U, -u in V, where u + (-u) = 0

Vector Space Axiom 5

1 Scalar: 1u = u

Vector Space Axiom 6

Associativity for Multiplication: (ab)U=a(bU)

Vector Space Axiom 7

Distribution (scalar): a(u+w)=au+aw

Vector Space Axiom 8

Distribution (vector): (a+b)U = aU + bU

Vectorspace Properties (6)

Cancelation law, zero unique, negative vectors unique, 0 vector and scalar, negative scalars

Inverse of a complex number

z conjugate / |z|²

Special Case of Span

when S is empty, span is 0 vector

How to prove two sets equal

Show both sets are subsets of each other (every a in a is in b and every b in b is in a)

row(A)

span{r₁,r₂,….,r_m} where r_i are rows of A

Subspace

closure under addition, scalar multiplication and 0 included in vector

Important Subspaces

0, subspace of itself, polynomials of degree n or less

For mxn Matrix let S be all solutions to Ax=b : S is a subspace of Fⁿ <=>

For mxn Matrix let S be all solutions to Ax=b : b = 0 (homogenous system) <=>

What is the span of subset S

S is subset of span(S)

If S subset of W

span(S) subset of W

For W subset of vector space: span(W) =

For W subset of vector space: W =

Every Span is a Subspace

Every Subspace is a span

By proposition 9

span(s) is the smallest subset contain S. If W subspace, S in W then W contains span(s)

Linear Independent

Distinct Vectors cannot form 0 unless trivial case

A subset B subset V

a) if A dependent, B also dependent

b) if B independent, A also independent

Proving contrapositive

If a then b is the same as if not a then not b

Proof for a Basis

span of set is equal to subspace and set is independent

S independent subset, w in vectorspace, w not in S. S u {w} independent <=>

S independent subset, w in vectorspace, w not in S. w not in span(S) <=>

Basis Theorem

Set W with span(s) where s is finite has a fintie basis and all bases of W have the same size.

Finite Dimensional

Vector or subspace with a finite basis

Dimension of a vector space

size of any of the basis (or infinite dimensional)

dim(P_n(F))

n+1

Nullspace/Kernel

{u∈Fⁿ|Au=0}

General Solution to Ax=0

x= t₁x₁+t₂x₂ +….+t_nx_n where t are free variables and vs form basis of null(A)

Given subset of a finite dimensional set (dim = n)

|s|>n: S can be reduced to a basis

|s|<n: S can be extended to a basis

|s| = n, w = span(s) <=> S independent

Dimension of a subspace

dimension is less than dimension of the vectorspace it is a subspace of

dimensions are equal if and only if sets are equal

col(a)

span of the columns of A

Basis for row(A)

Non-zero rows of R (after row reduction)

Basis for col(A)

Columns of A that correspond to leading entries in original matrix (before row reduction)

Intersection of two subspaces

Also a subspace

Union of two subspaces

Usually NOT a subspace, but their span IS

Sum of two subspaces

{u+w| u ∈ U, w∈W}

u+w

= span(U u W) where u and w are both subspaces of u+w

Direct Sum

Every vector in Vectorspace has a unique decomposition in the form v = u+w (hint: the intersection of u and w should be 0)

Dimension of U+W

dim(u+w) = dim(u) + dim(v) - dim( u ∩ w)

Lagrange Polynomial

l_i(x) = ((x-a₀)/(a_i-a₀))*((x-a₁)/(a_i-a₁))*…..*(x-a_n)/(a_i-a_n) (FOR ALL EXCEPT a_i-a_i

Lagrange Interpolation

f(x) = (n)∑(i=0) (b_i*l_i(x))

Linear transformation

1. T(u₁+u₂)=T(u₁)+T(u₂)

2. T(cU) = cT(U)

Properties of Linear Transformations

1. T(0) = 0

2. see image

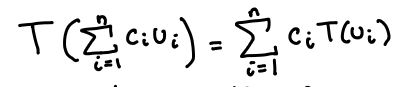
Zero Transformation

all vectors go to 0

Identity Transformation

All vectors go to themselves

kernel/nullspace Transformations

{u in U } T (u) = 0 } (subset AND subspace of U)

image/range Transformations

{ v in V | there exists u in U such that v = T(u) } (subset AND subspace of V)

rank(T)

dim(im(T))

nullity(T)

dim(ker(T)) (aka number of free variables)

U= span(a),What does T(a) do

Then T(a) spans im(T) (But is not necessarily a basis)

Injective (one-to-one)

No two vectors map to the same result OR if they do they are the same vector

Surjective (onto)

Every vector maps to a resulting vector in codomain

Bijective

Both injective and surjective

finite not injective domains

x > y

finite not surjective domains

x < y

Domains equal

if it satisfies one, it satisfies the other as well

Invertibility if

also bijective

How to check if T injective

nullity = 0

How to check if T surjective

rank(T) = dim(v)

Isomorphism

Linear and bijective transformation

Coordinate vector [v]_b

Vector where elements correspond to coefficients of linear combination of vectors in basis b.

Transformation between vectorspaces

Exactly one T: V→W such that T(v_i)=w_i

Function that computes the coordinates in a vector space to coordinate vectors

This function is an isomorphism (allows us to do computations and then revert back)

Composition of Two Linear Functions

Is also linear

Composition of two isomorphic Functions

is also isomorphism

Inverse of an isomorphic function

is also isomorphic

Vectorspaces with finite dimensions equal to eachother

are isomorphic between eachother

For T: U→ V: [T]_a^b

Computes transformation in alpha coordinates and outputs them as beta coordinates (alpha is basis of U, beta is basis of V)

Inverse Tranformation Matrix

Take Inverse of the Transformation Matrix

T: U → V, S: U → W both linear, composition matrix [SoT]

[SoT]_a^y = [S]_b^y[T]_a^b

Similar Matrices A, B

There is an invertible Q such that Q^-1AQ= B

Transformation matrix is similar to another matrix

There is some basis such that the matrix is equal to the transformation matrix in that basis.

L(V,W) vectorspace over F

Define addition as linearity and scalar multiplication as linearity

For L(V, W) with dim V = n, dim W = m, The linear transformation from L(V, W) to the matrix space is defined by the transformation matrix taking a coordinates and outputting b coordinates and is isomorphic which means

Every linear transformation from V to W can be uniquely represented by an m×n matrix. Every m×n matrix corresponds to a unique linear transformation from V to W.

Inner Product: Linearity in First Component

<u+v, w> = <u,w> + <v,w> & <cU,V> = c<U,V>

Inner Product: Conjugate Symmetry

<v, u> = (conjugate: <u, v>) (does nothing in R)

Inner Product: Positive Definite

for u ≠ 0, <u,u> > 0

Satisfies Inner Product

linearity in first component, conjugate symmetry and positive definite

Conjugate Linearity in Second Component

<u, v+w> = <u, v> + <u, w> & <u,cv> = (conjugate c)<u,v>

Standard Inner Product on Fⁿ

Dot product: <u, v> = ∑a(conjugate b)

Standard Inner Product on Polynomials

Choose some interval and define f and g in P(R) such that inner product is integral of f*g evaluated on the interval

Conjugate of a matrix

Every element is conjugated

Adjoint of A

A* = (conjugate A, transposed) = (A transpose, conjugate) (this means A* = A^T for real numbers)

Frobenius inner product

tr(AB*)

Norm/Length

||U|| = √<u,u>

||cU||

|c|||U||

Cauchy Schwarz Inequality

|<u,v>| ≤ ||u||||v||

If ||u||||v|| equal to absolute value of inner product

vectors must be scalar multiples of eachother

Triangle Inequality

||u+v|| <= ||u|| + ||v||

Angle

cos θ = <u,v> / ||u||||v||

Orthogonal Vectors

Dot product is 0

Orthogonal Set

all vectors in a set are orthogonal to eachother

Orthonormal Set

Norm of all vectors are 1 and orthogonal set

Orthogonal Basis

basis where all vectors are orthogonal to eachother

Fact about orthogonal set

all orthogonal sets are linearly independent

Fourier Coefficients of U relative to a = {v….v_n}

<u, v_i>/<v_i,v_i>