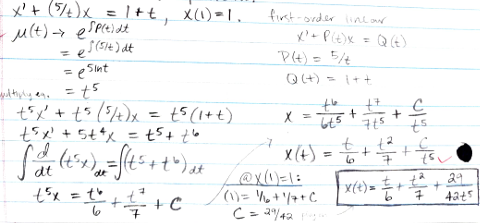Differential Equations Test #1

Sections 1.1-1.5

Linearity: Dependent variable “y” and its derivatives (dy/dx, d²y/dx², etc.)

Linear

Linearity: y², y³, sin(y), etc.)

Non-linear

Homogeneity: Dependent variable “y” and its derivatives are linear only.

Ex. dy/dx + 3y =0

d²y/dx² + 4(dy/dx) +3y = 0

Homogenous

Homogeneity: Dependent variable “y” and its derivatives are non-linear only.

Ex. a_n^x(dⁿy/dxⁿ) + a… = f(x)

Non-homogenous

A differential equation involving partial derivatives with respect to more than one independent variable.

Partial differential equation, PDE

A differential equation involving only ordinary derivatives with respect to a single independent variable.

Ordinary differential equation, ODE

Models that often yield an equation that contains some derivatives of an unknown function.

Differential equation

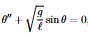
Determine the order and linearity of the following DE.

Second-order nonlinear

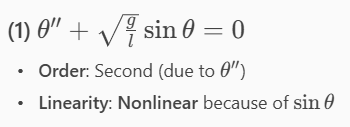
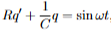
Determine the order and linearity of the following DE.

First-order linear

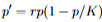
Determine the order and linearity of the following DE.

First-order nonlinear

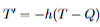
Determine the order and linearity of the following DE.

First-order linear

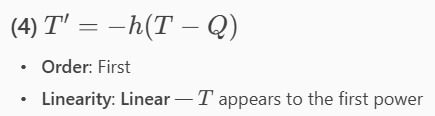
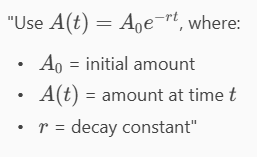
Radioactive Decay: Four grams of a sample of a radioisotope decay to 0.8 grams in 3 years.

(a) What is the decay constant r?

(b) What is the half-life, or the time when only half of the sample remains?

Hint: Recall the relationship b/w half-life and decay constant … T_1/2 = ln(2)/r

r=0.5365, t=1.29

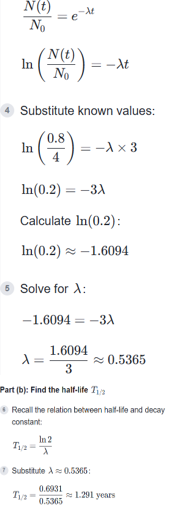
Draw the direction field and nullclines of x′ = −tx + x2 = x(x − t).

Hint: rewrite DE, set x’ =0, analyze direction at various points, and sketch t,x values.

Solve the IVP x′′ = t+2 with x(0)=1 and x′(0)=0.

Hint: Integrate to find x’(t), apply condition, integrate to find x(t), and apply initial condition.

x(t) = (t³/6)+t²+1

Solve the IVP x′ = t/x with x(2) = 1.

Hint: This is a separable DE, integrate both sides, and apply condition.

x(t) = sqrt(t²-3)

Solve the IVP x′ + (x/t) = 1 with x(1) = 3.

x(t) = (1/2)t + (5/2)/t

Solve x′ + 2x = sin(t).

(2/5)sin(t) - (1/5)cos(t) + Ce^-2t

Find all equilibrium points and determine their stabilities for dy/dx = (1-e^2y)(y−1)²(y−2).

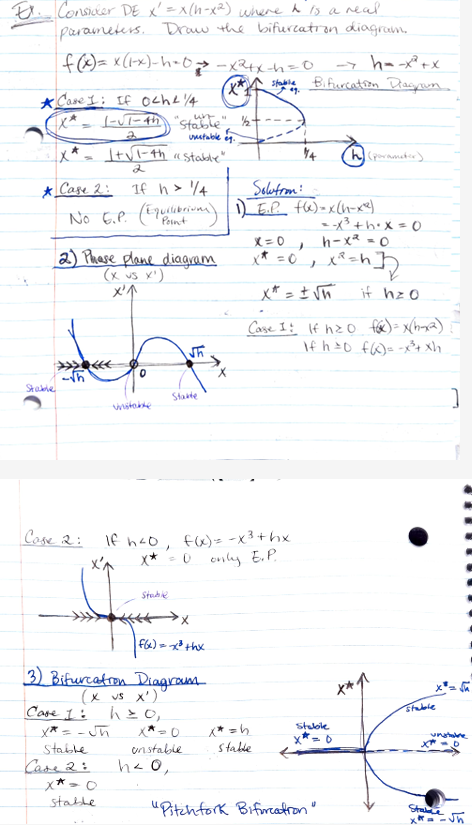
Consider DE x′ = x(h − x²) where h is a real parameters. Draw the bifurcation diagram.

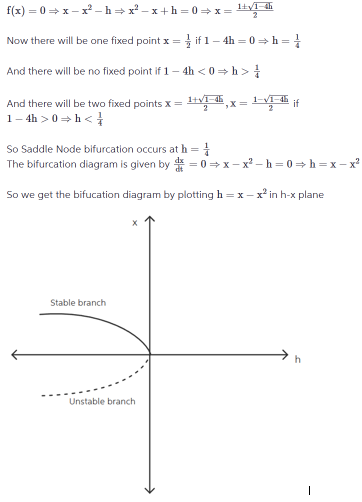
Draw the bifurcation diagram of x′ = x(1−x) − h.

Which of the following functions is a solution to the DE x’ = -x²: 

a. x(t)= 1/t

b. x(t)= 2/t

c. x(t)= 1/(t-2)

Hint: Compute derivatives, compute -x(t)², and compare sides.

a, c

Find a solution x=x(t) of the equation x’+2x = t²+4t+7 in the form of a quadratic function of t, that is, of the form x(t)= at²+bt+c, which are to be determined.

Hint: Compute x’(t), sub in x’(t) and x(t) values, expand & simplify, and find a/b/c.

x(t)= (1/2)t² + (3/2)t + (11/4)

Find values of m for which x(t)= t^m is a solution to t²x’’- 6x = 0.

Hint: Complete derivative, plug in values, and solve quadratic equation.

-3, 2

Find the values of λ for which x(t)= e^λt is a solution of the differential equation 2x’’-5x’-3x=0.

Hint: Complete derivatives, plug in values, and solve quadratic equation.

3, -1/2

In deep water, the intensity of light I=I(x) at a depth x meters below the water surface is modeled by the equation I’=-1.4I. At what depth is the light intensity 1% that at the surface?

Hint: Solve the DE, integrate, and find the depth.

3.29 meters

0, 4

Draw several isoclines of the DE x’= x²+t², and from your plots, determine approximately the graphs of the solution curves.

Draw the nullclines for the equation x’= 1-x². Graph the isoclines, or the locus of points in the plane where the slope field is equal to -3 and +3.

1, -1

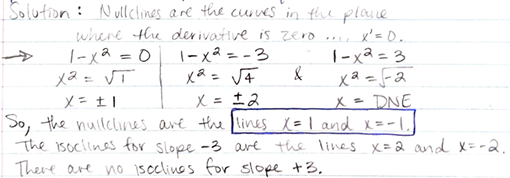
Find the general solution to the DE x’= tcos(t²). Find the particular solution satisfying the initial condition x(0)=1, and plot the solution on the interval -5 ≤ t ≤ 5.

Hint: Integrate, assign u values, and plug into general solution.

x(t)= (1/2)sin(t²)+C

x(t)= (1/2)sin(t²)+1

Find a function x(t) that satisfies the initial value problem x’’= -3sqrt(t), x(1)=0, and x’(1)=2.

Hint: Integrate, integrate again, and apply conditions.

x(t)= (-4/5)t^5/2 + 4t - (11/5)

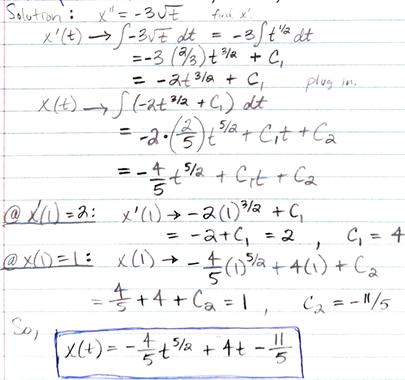
Use the method of separation of variables to find the general solution to the following differential equations:

a. y’= 1+y²

Hint: rewrite, separate variables, and integrate.

b. x’= ax+b,   where a,b > 0

Hint: rewrite, integrate, and solve for x.

c. Q’= Q/(4+Q²)

Hint: Separate variables and integrate.

a. y= tan(t+C)

b. x(t)= Ce^at- (b/a)

c. 4ln|Q| + (1/2)Q² = t+C

Solve y’= r(a-y), where r and a are constants.

Hint: separate variables, integrate, and solve for y.

y(t)= a - Ce^-rt

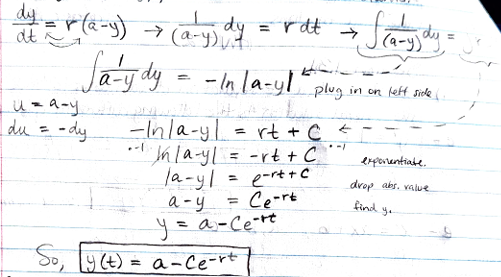
Solve the IVP and find the interval of existence.

dy/dt= 1/(2y+1), y(0)=1

Hint: separate variables, integrate, apply initial conditions, solve for y, and arrive at the interval of existence.

y(t)= (-1± sqrt(4t+9))/2

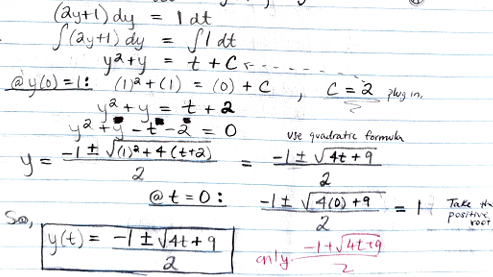
Solve x’= x(4+x) subject to the initial condition x(0)=1.

Hint: rewrite, separate variables, use partial fractions, integrate, solve for x, and apply initial condition.

x(t)= 4Ce^4t/1-Ce^4t

x(t)= 4e^4t/5-e^4t

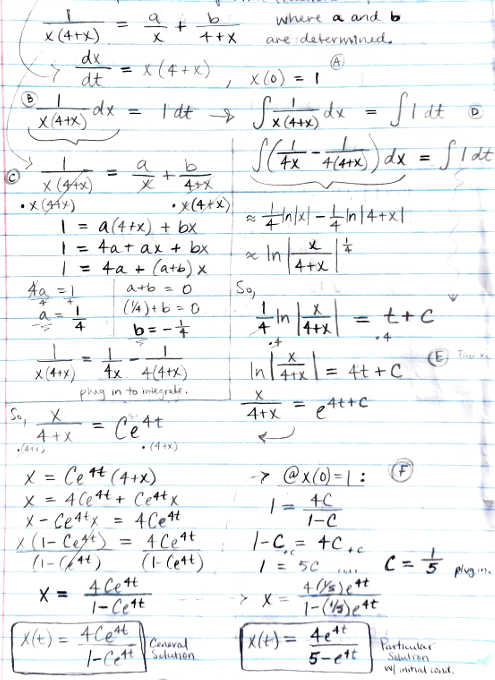
A small turkey at room temperature, 70°F, is placed in an oven at 350°F. If h=0.42 per hour is the heat loss coefficient for turkey meat, how long should you cook the turkey so that it is uniformly 200°F? Comment on validity of assumptions.

Hint: Newton’s law of cooling, separate variables, integrate, apply initial condition, and solve for time.

1.49 hours

The body of a murder victim was discovered at 11am. The medical examiner arrived at 11:30 a.m. and found the temperature of the body was 94.6°F. The room temperature was 70°F. One hour later, in the same room, he took the body temperature again and found that it was 93.4°F. Estimate the time of death.

8:30am

Classify the first-order equations as linear or nonlinear.

a. 7t²x’ = 3x-2t

b. xx’ = 1-tx

c. (x’)²+tx = sqrt(t+1)

linear, nonlinear, nonlinear

Solve the IVP:

x’+(5/t)x = 1+t, x(1)=1

x(t)= (t/6) + (t²/7) + (29/42t⁵)