T-tests

The T-test is used to

compare 2 means

For one sample compared to a population use

One sample t-test

One sample t-test

Compare the blood pressure of one group to a theoretical or published value

For two sample groups use

Unpaired t-test

Paired t-test

Unpaired t-test

comparing two independent, but similar groups

aka Student’s t-test

Compare the blood pressure of two groups of similar individuals (adult men’s bp vs. adult women’s bp)

Paired t-test

comparing the a group before an intervention to the same group after an intervention

Compare the blood pressure of a group before and then after climbing ten flights of stairs

T-test Assumptions

1.Normal/Gaussian distribution

2.Randomly sampled

3.Equal variances (see below)

4 Data measured on interval or ratio scale ^

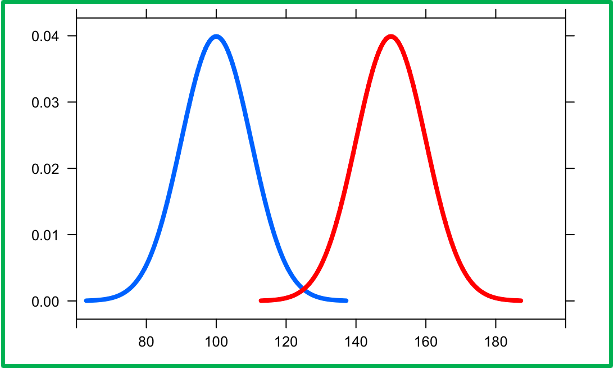
Normal Distribution with equal variances

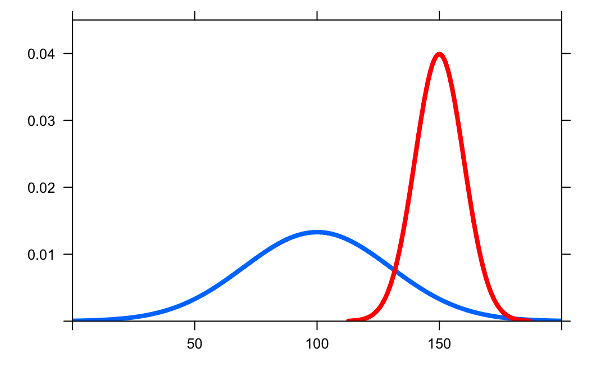
Normal Distribution with different variances

Comparing Means

•Comparing the average and how widely spread it is

•Statistical significance for comparing means is based on the relationship between mean and the variance

effect size

•difference between group means indicating a degree of separation between them

Variance measures tell us how variable scores are

within each group

One-Tailed Test

•A directional hypothesis might call for a one-tailed test

•In order to use a one-tailed test, there must be a specific reason why you would only expect a difference in one direction

•The entire rejection (critical) region (5% in this case) is on one side of the distribution

One tailed tests are used when there is a ___ hypothesis

directional

Two-Tailed Test 2 possible outcomes

If there is a possibility that the difference could be in either direction, use two-tailed test, even if your hypothesis is directional

2 tailed tests are __ conservative than one tailed

More

For 2 tailed tests, the rejection (critical) region (5% in this case) is X__ between both tails of the distribution

split. 2.5% probability a result will fall in either critical region

unpaired t tests need

1.Two normally distributed but independent populations

2.Two sample means

3.Two sample standard deviations

4.Both sample sizes (n)

5.Table of critical t-values or a stats program

A t-test is significant if

The p-value is less than 0.05 (alpha)

and

The absolute value of the t-statistic is greater than the critical value (always use in absolute values, take away neg signs)