ap calc ab exam
1/78
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
79 Terms
derivative
slope of the graph at any particular point
trapezoid formula
A=(a/2+b+c+d+e/2)Δx
vertical asymptotes
occur where the denominator approaches 0 and the numerator does not
horizontal asymptotes
found by comparing the degree of the numerator and the degree of the denominator (or the lead coefficients)
non-horizontal asymptotes
found by doing long division
LIMIT RULES
LIMIT RULES
limit of a sum is equal to the sum of the limits
\lim_{x\rightarrow a}\left(f\left(x\right)+g\left(x\right)\right)=\lim_{x\rightarrow a}f\left(x\right)+\lim_{x\rightarrow a}g\left(x\right)
limit of a constant times a function equals the constant times the limit of the function
\lim_{x\rightarrow a}\left(c\cdot f\left(x\right)\right)=c\cdot\lim_{x\rightarrow a}\left(f\left(x\right)\right)
the limit of a product equals the product of the limits
\lim_{x\rightarrow a}\left(f\left(x\right)\cdot g\left(x\right)\right)=\lim_{x\rightarrow a}\left(f\left(x\right)\right)\cdot\lim_{x\to a}\left(g\left(x\right)\right)
the limit of a quotient equals the quotient of the limits
\lim_{x\to a}\frac{f\left(x\right)}{g\left(x\right)}=\frac{\lim_{x\to a}\left(f\left(x\right)\right)}{\lim_{x\to a}\left(g\left(x\right)\right)}
the limit of a quotient DNE if the denominator is zero while the numerator is not zero
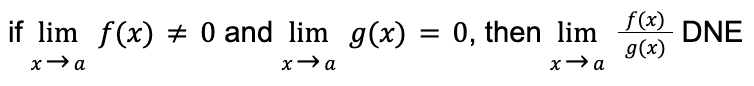
the value of a limit as x➡a is the same as the value of the polynomial at x=a
\lim_{x\to a}p\left(x\right)=p\left(a\right)
cusp
a point at which the function is continuous but the derivative of the function is discontinuous
intermediate value theorem
if f is continuous over [a,b] and y is a number between f(a) and f(b), then there is some number c in the interval [a,b] such that f(c)=y
difference quotient
\frac{f\left(x\right)-f\left(c\right)}{x-c}
calculating a derivative
take the limit of the difference quotient
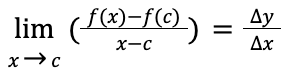
mathematical definition of a derivative
\lim_{\Delta x\rightarrow0}\frac{f\left(x+\Delta x\right)-f\left(x\right)}{\Delta x}
derivative of a power function
if f(x)=xn then f'(x)= nxn-1
derivative of a sum
the sum of the derivatives (same as limits rule)
derivative of constant times a function
\frac{d}{\differentialD x}kf=kf^{\prime}
derivative of a constant
0
linear approximation
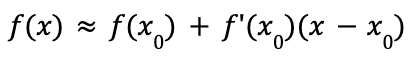
derivative chain rule
derivative of the outer function with respect to the inner times the derivative of the inner function
derivative product rule
first times the derivative of the second plus second times the derivative of the first: uv'+u'v
quotient rule
low d high - high d low over low times low
derivative of sin(x)
cos x
derivative of cos(x)
-sin x
derivative of tan(x)
(sec x)(sec x)
derivative of csc(x)
-csc x cot x
derivative of sec(x)
sec x tan x
derivative of cot(x)
-csc² x
rate of change practical consequence
the slope of f at any point (x,y) is the reciprocal of the slope of f' at the corresponding point (y,x)
extreme value theorem
if f(x) is continuous on [a,b], then f(x) has both an absolute maximum and minimum on [a,b]
rolle's theorem
between 2 zeros of a function, there is a place where the slope is zero
requirements
1. a function is differentiable on the open interval (a,b)
2. the function is continuous at x=a and x=b
3. f(a)=f(b)
mean value theorem
at some point in the interval [a,b] there is a place where the slope of the curve equals the slope of the secant line
if f is rising...
f' is positive
if f is rising at an increasing rate...
the value of f' gets larger
if f' has a positive slope
f'' has a positive value
if f is concave up
f' is increasing, and f'' is positive
average velocity
Δx/Δt
instantaneous velocity
dx/dt
speed
how fast something is moving (absolute value of velocity)
velocity
how fast something is moving and in what direction
constant of integration
"+ c"
definite integral
the area under a graph
integral multiplication rule
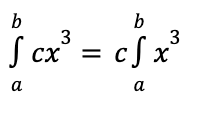
integral power rule
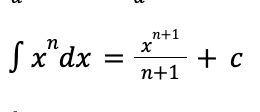
the integral of the sum of functions...
is equal to the sum of their integrals
fundamental theorem of calculus
\int_{a}^{b}\!f^{\prime}x\,dx=f\left(b\right)-f\left(a\right)
integrals from a higher to lower number
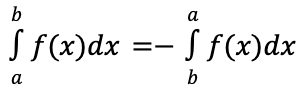
the sum of two adjacent areas
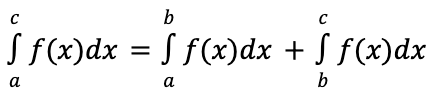
even function
symmetrical about the y-axis
integral properties of even function
upper and lower limit are equal and opposite. definite integral includes the same area on the left of the axis as it does on the right
odd function
symmetrical about the origin
integral properties of odd function
upper and lower limit are equal and opposite. definite integral includes the same area on one side above the axis as it does on the other side belwo the axis
integrand
expression between integral and "dx"
average value
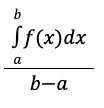
derivative of ln(x)
1/x
integral of ln(x)
x ln x - x + c
when differentiating b^x
multiply by ln b
when integrating b^x
divide by ln b
logarithmic differentiation
take the logarithm of both sides
use the properties of logarithms to change the exponent to multiplication
differentiate both sides with respect to x. don’t forget that the chain rule applies
∫sin(x) dx
-cos x + c
∫cos(x) dx
sin x + c
∫tan(x) dx
-ln |cos x| + c = ln |sec x| + c
∫cot(x) dx
- ln |csc x| + c = ln |sin x| + c
∫sec(x) dx
ln |sec x + tan x| + c
∫csc(x) dx
ln |csc x - cot x| + c = - ln |csc x + cot x| + c
l'hospital's rule
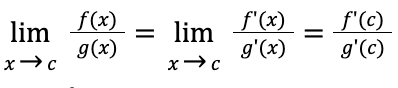
volume of a paraboloid
dV = (circumference)(dA)
plane slicing a paraboloid
r2 is some function of x. h is “dx”
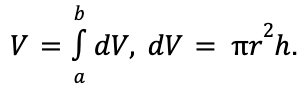
cylindrical shells
dV=2\pi x\left(h-y\right)\differentialD x or vice versa
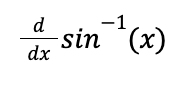
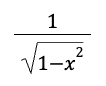
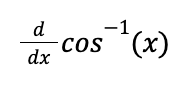
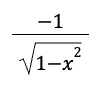
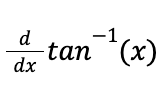
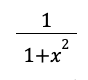
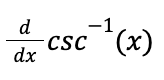
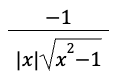
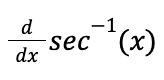
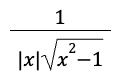
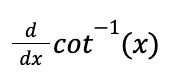
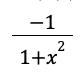
riemann sum formula
A method for approximating the total area under a curve using finite sums of rectangle areas.