phy D3 motion in magnetic fields

motor effect

• when a current-carrying wire is placed in a magnetic field, the magnetic interaction between the conventional current and magnetic field results in a force.

• F = BIL sin theta

  • sin theta is between B and I → max force at 90, no force at 0 (parallel)

  • units of B is tesla

tesla

the magnetic flux density of 1 tesla will cause a wire of length 1m carrying current of 1A that is perpendicular to the field to experience a force of 1N

magnetic field due to current carrying wire

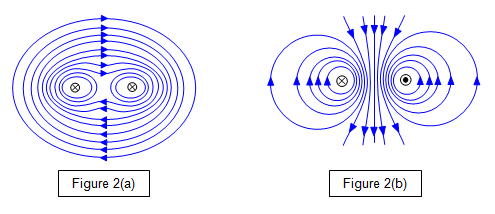
magnetic field due to two parallel wires

two wires will attract if same direction, repel if opposite

parallel current-carrying conductors

the current in each wire produces a magnetic field, the other wire is in the field so it experiences a force.

force per unit length calculated using Ampere’s force law: F/L

direction of magnetic field at any point is the tangent to the circular field.

• magnetic field is out of paper

• even though current rotates, angle between B and I is still perpendicular → sin theta same, magnitude of F same

charges in magnetic fields on a microscopic level

• each electron in the wire experiences force as it travels through magnetic field → note electron flow is opposite to conventional current

• sum of forces causes total force on wire F = BIL

• if per electron, F=Bqv

motion of charged particle in magnetic field

• F=qvBsintheta, if theta (angle between B and I) = 90, undergoes circular motion

  • magnitude of v unchanged but direction changes by FLHR

  • F provides centripetal force, work done = 0 since v is perpendicular to F at all times

  • magnetic force = centripetal force → r = mv sintheta/qB

• if charged particle moves through magnetic field at an angle, experiences helical motion

  • perpendicular component vsintheta causes circular motion

  • parallel component vcostheta is uniform

motion of charged particle in crossed electric/magnetic fields

• if Fb and Fe balanced, Bqv = qE → v=E/B

  • mag into paper + pos charge to the right → Fb up

  • Fe down because positive charge in uniform electric field (parallel plates)

• constant velocity + direction if balanced

motion of particle in uniform electric field

• projectile motion → parabolic path (similar to kinematics when gravity)

• F not perpendicular to v! just downwards all the time

condition for charged particle to experience force in a magnetic field

velocity of charged particle must have a component perpendicular to the direction of the magnetic field

change in velocity of charged placed in magnetic field

ZERO. force perpendicular to velocity, so no increase in velocity!!! acceleration just changes direction!!!

factors affecting potential energy

• distance increase, potential energy increase

• potential energy of an object decreases as it moves naturally in a force field