CHAPTER 3: Probability and Probability Distributions

• a quantitative measure of uncertainty

• a number that expresses the strength of our belief in the occurrence of an uncertain event

PROBABILITY

any process that allows researchers to obtain observations. It is any process that can be repeated under basically same conditions and yields well defined outcomes.

Random experiment

the set of all possible outcomes of a random experiment

Sample space (S)

• Elements of the sample space are called ___

• the number of sample points is denoted by __

• sample points

• n(S)

A subset of the sample space is called ___

event

Three Types of Probability

1. Classical Approach

2. Relative Frequency Approach

3. Subjective Probability

Based on the idea that certain occurrences are equally likely, that is, we assume that in a given experiment, all the sample points in the sample space have equal chances of occurring

Classical Approach

Also called a priori probability, which means we can state the answer in advance without performing the experiment

Classical Approach

An experiment is conducted or observed in large number of times that an event actually occurs, that is, probabilities are determined based on experimental approach

Relative Frequency Approach

This law states that “as a procedure is repeated again and again, the relative frequency probability of an event tends to approach the actual probability”

Law of Large Numbers

a variable that has a single numerical value (determined by chance) for each outcome of a random experiment

random variable

Random Variable 2 Types

• Discrete Random Variable

• Continuous Random Variable

has either a finite number of values or a countable number of values

Discrete Random Variable

has infinitely many values which can be associated with measurements

Continuous Random Variable

the listing of all possible value that a random variable can take on together with their corresponding probabilities.

Probability distribution

The mean of a random variable X is also termed as the expected value of X, written as ___

E(𝑋)

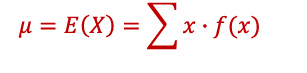
The variance of a random variable, written as ___

V(𝑋)

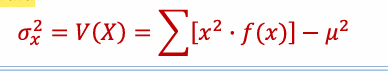
Probability Distribution

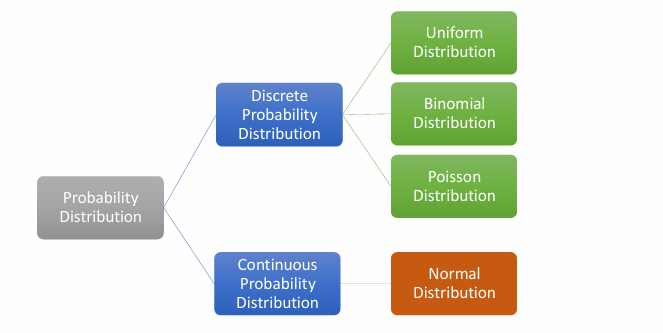
Discrete Probability Distributions Types

• Uniform Distribution

• Binomial Distribution

• Poisson Distribution

outcomes with equal probabilities

Uniform Distribution

two possible outcomes

Binomial Distribution

counts or discrete outcomes

Poisson Distribution

• Simplest of all the discrete probability distributions

• “Rectangular distribution”

• Random variable X assumes the values 𝑎1,𝑎2,…,𝑎𝑁 with equal probabilities

Uniform Distribution

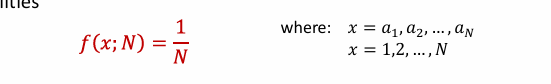
Deals with random variables with only two possible outcomes

Binomial Distribution

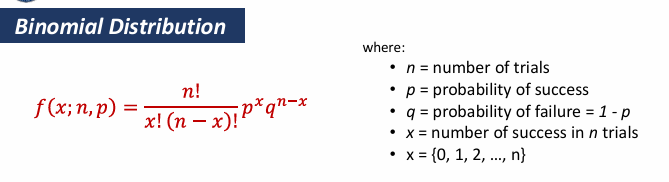
• Deals with random variables that involve counts in an interval

• Applies to occurrences of some event over a specified interval

• Used for describing behavior of rare events (with small probabilities)

Poisson Distribution