AP calculus AB formulas

Definition of Limits

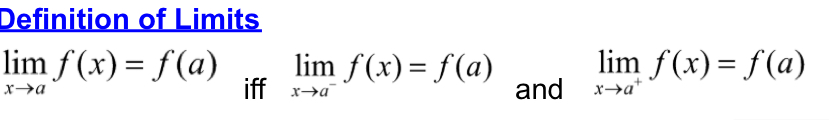
Limit laws

sum law, difference law, constant multiple law, product law, quotient law, power law, and root law

Sum Law

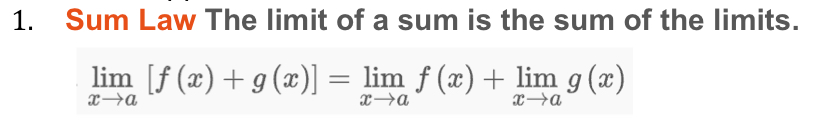
Difference Law

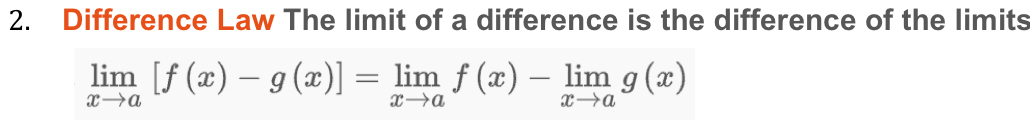
Constant Multiple Law

Product Law

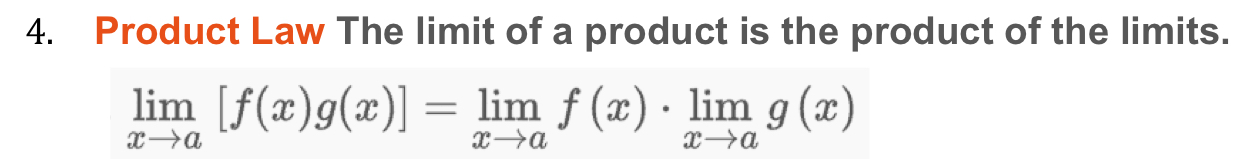
Quotient Law

Power Law

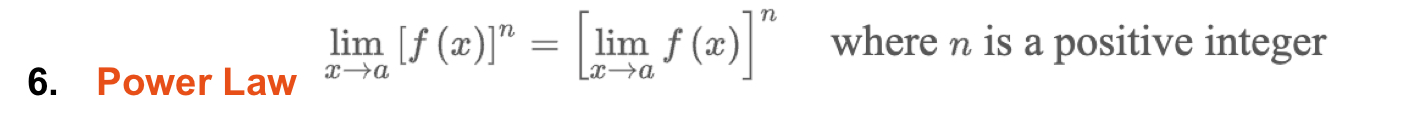
Root Law

Continuity

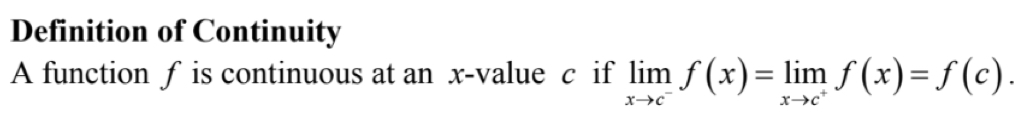
Types of Discontinuity

Types of discontinuity include removable, jump, and infinite discontinuity.

Horizontal Asymptotes

Vertical Asympotes

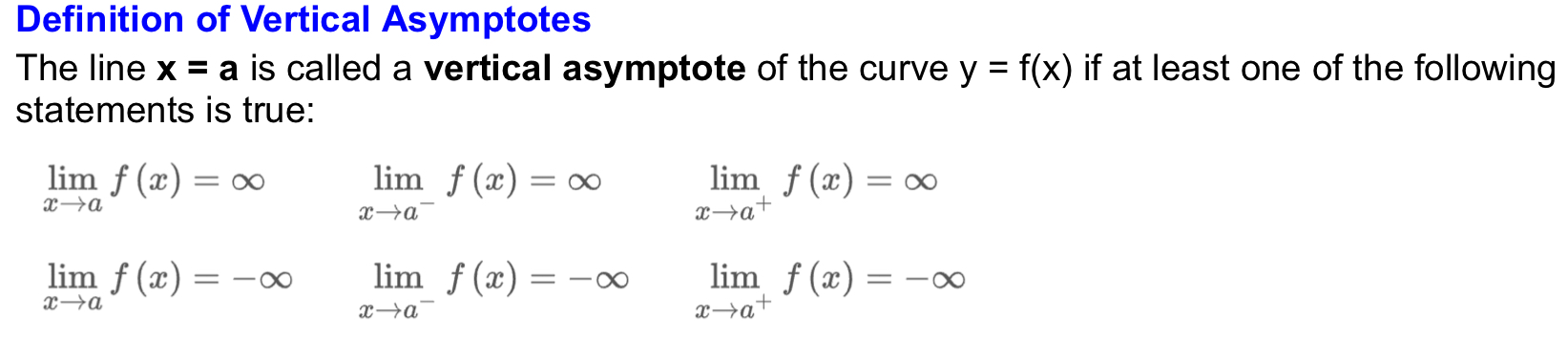
Special Trig Limits

Trig Identities

Tangent line

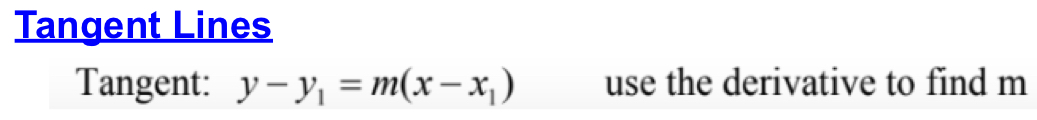
Average Rate of Change (AROC)

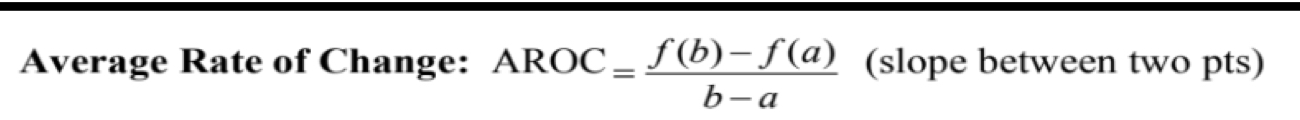
Instant Rate of Change (IROC)

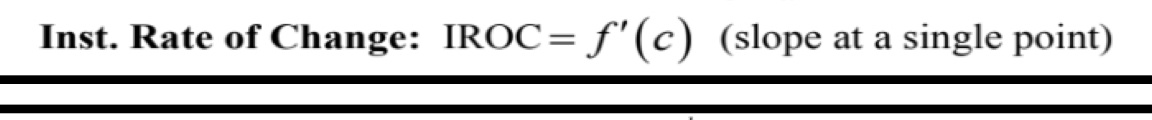
Average Value of a Function

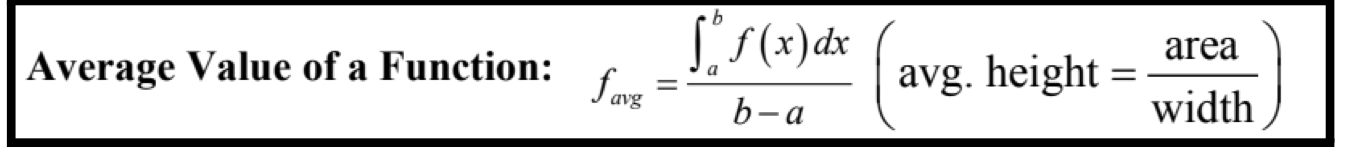
Intermediate Value Theorem (IVT)

Extreme Value Theorem (EVT)

Squeeze Theorem

Mean Value Theorem (MVT)

Mean Value Theorem (MVT) There is a number c in (a,b) such that

5' (c) = 5(b) -5(a)

(for f continuous on [a, b] and differentiable on (a, b))

b-a

Informally:

The Mean Value Theorem states that given the right

a

conditions of continuity and differentiability, there will be at least one tangent line parallel to the secant line.

In still other words: The instantaneous rate of change (slope of tangent) will equal the average rate of change (slope of secant) at least once.

Definition on Derivative

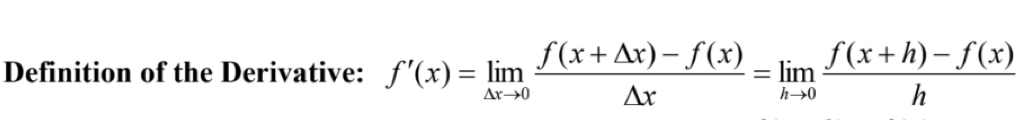
Derivative at a single point

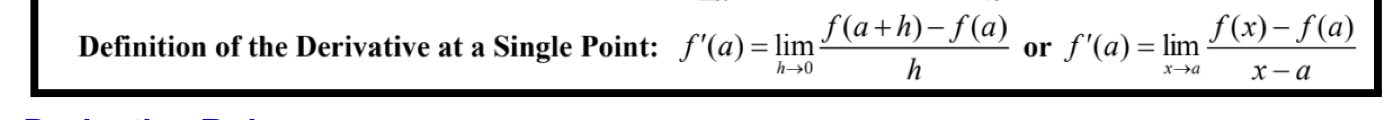
Derivative Rules

Power Rule, Log Rule, Exponential Rule, Trig Rule, Inverse Trig Rule

Power rule

Log rule 1

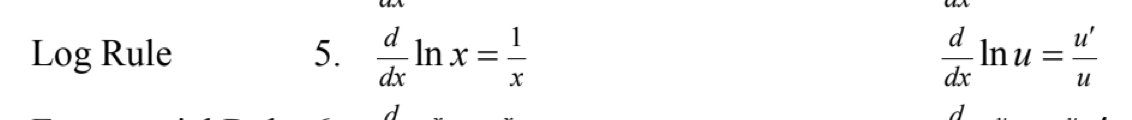
Exponential Rule 1

Trig Rule 1

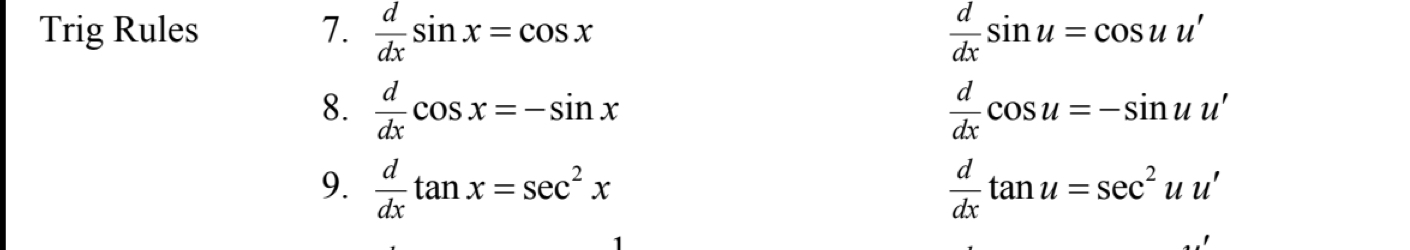
Inverse Trig Rule

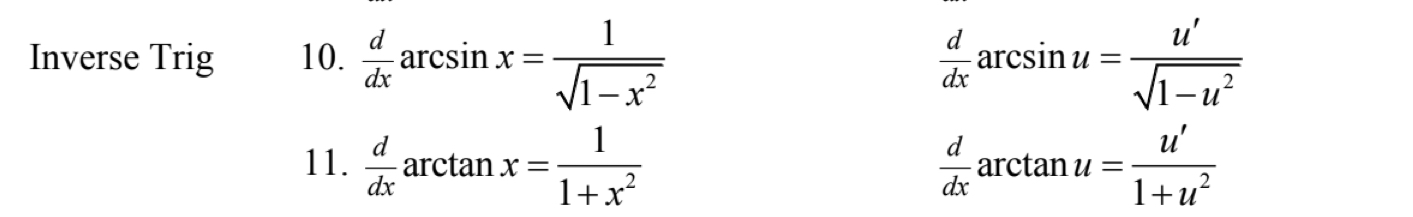
Exponential Rule 2

Log Rule 2

Trig Rule 2

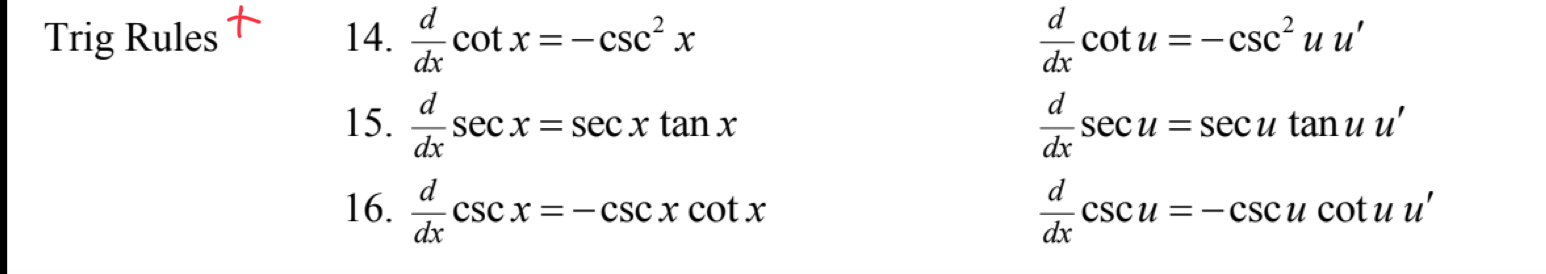
Product Rule

Quotient Rule

Chain Rule

Implicit Differentiate this : x² + y² = 36

A technique used to differentiate equations that define y implicitly in terms of x, treating y as a function of x and applying the chain rule appropriately.

Derivative of Inverse Function

First Derivative Test

Second Derivative test

Position velocity and acceleration (Der & Int)

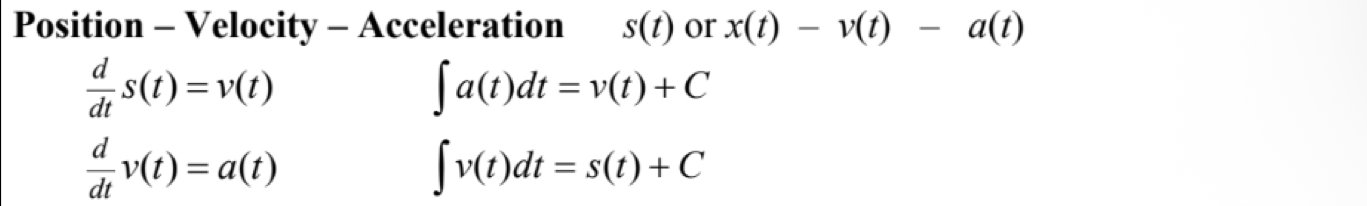
Velocity rules + speed

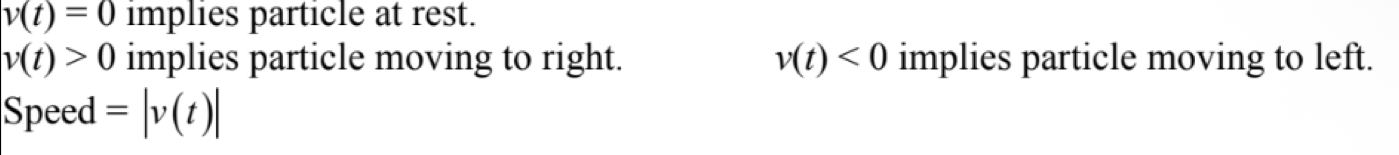
Displacement & total distance

L’Hospital’s Rule

Left Riemann Sum

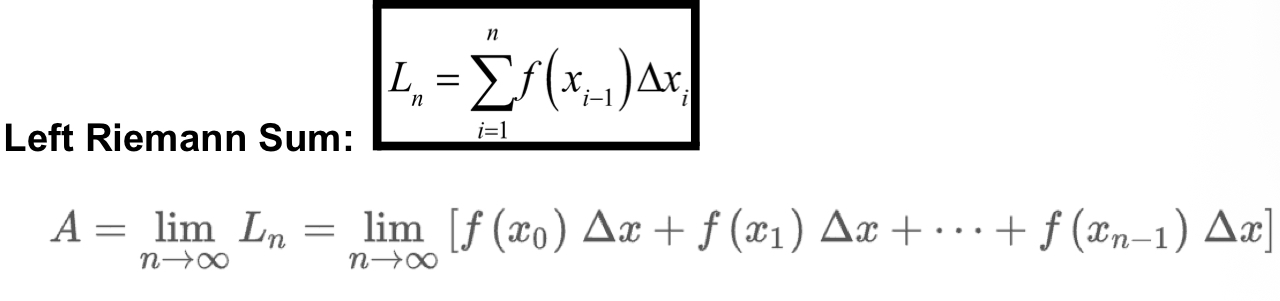
Right Riemann Sum

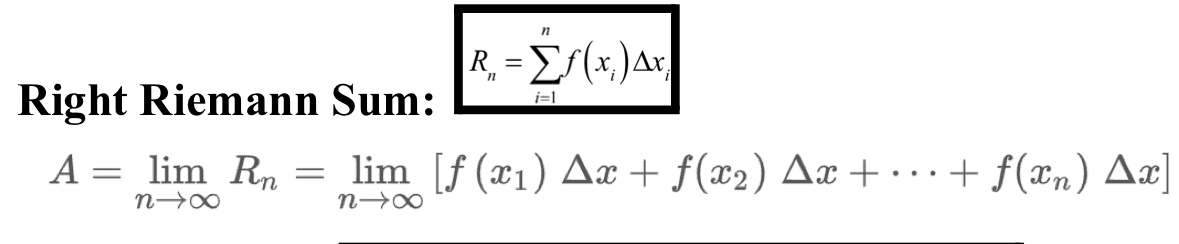
Midpoint Riemann Sum

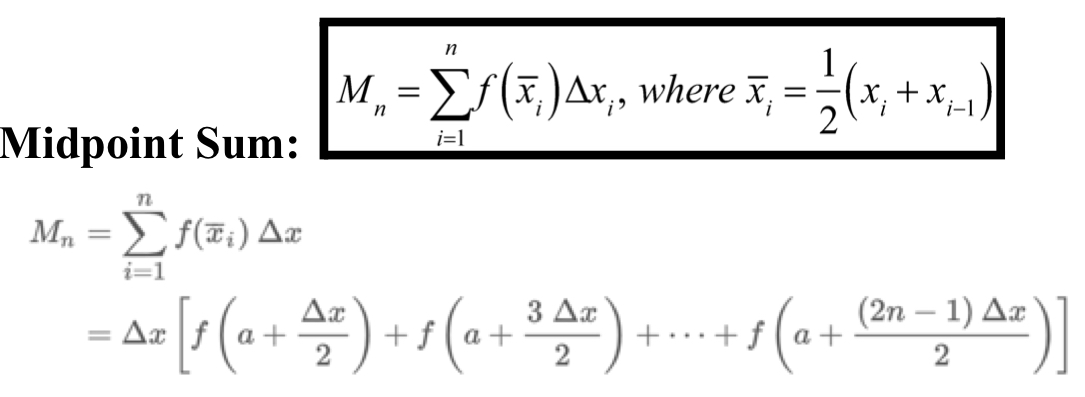
trapezoidal Riemann Sum

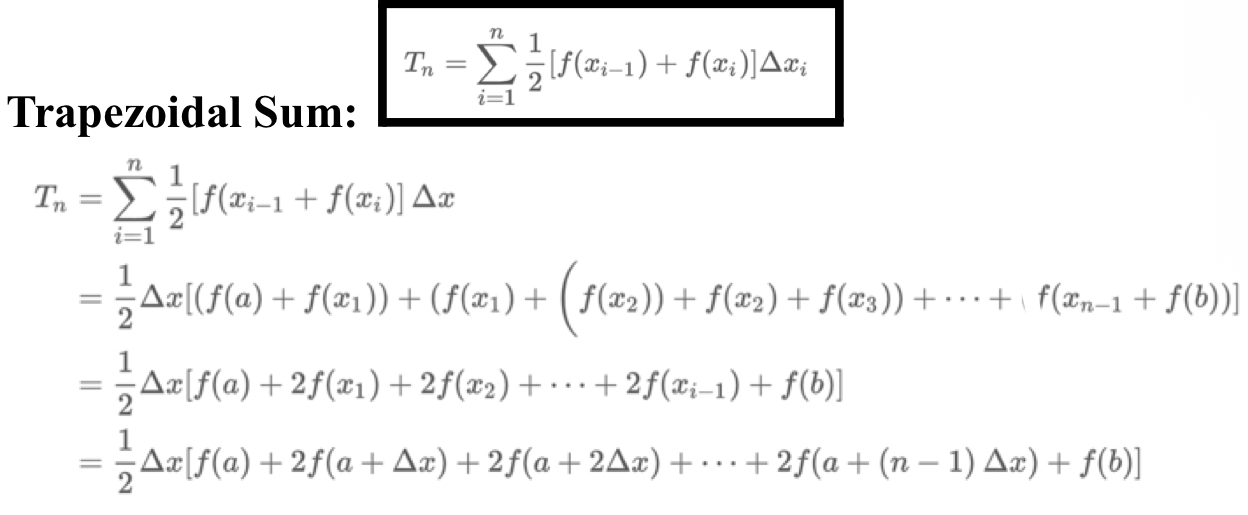
Lower Sums

Rectangles that lie under the graph

Upper sum

Rectangle that extend above the graph

Integral to Limit

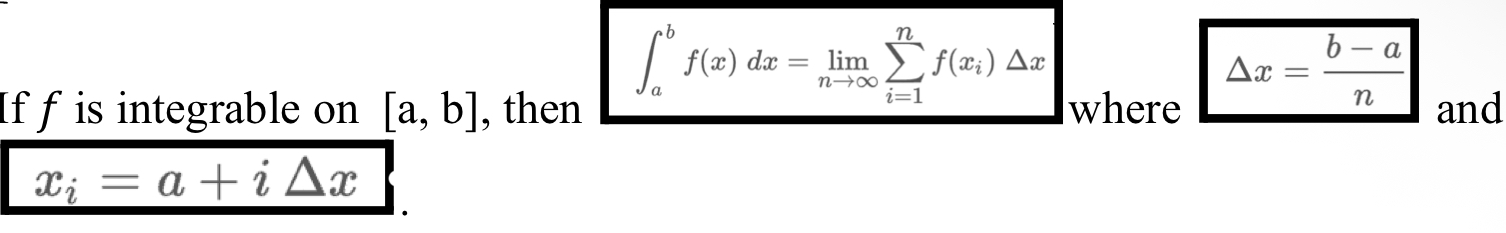
Tan Line Approximation

Over/Under approximation

Two Types of Areas Between Curves

(Top-Bottom) & (Right-Left)

(Top-Bottom)

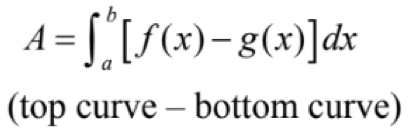
(Right-Left)

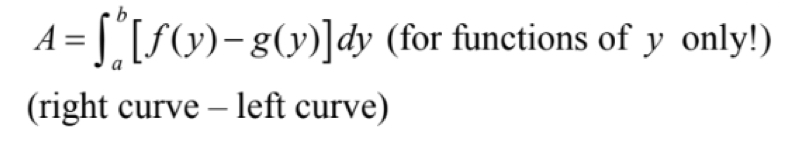
3 Volumes of a Solid

Disc Washer, and Known Cross Sections

Disc

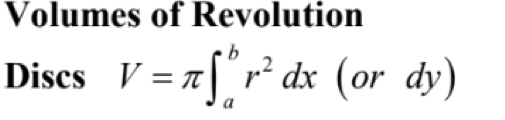
Washer

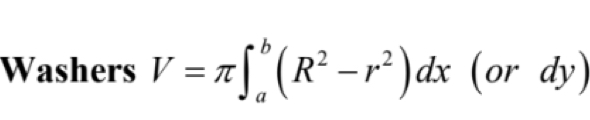
Known Cross Section

Substitution Rule

Even

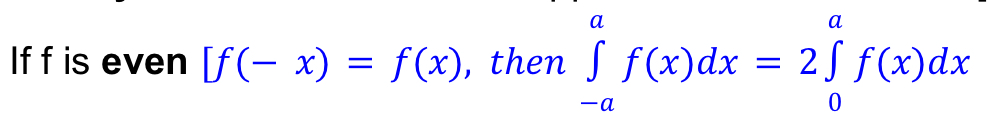
odd

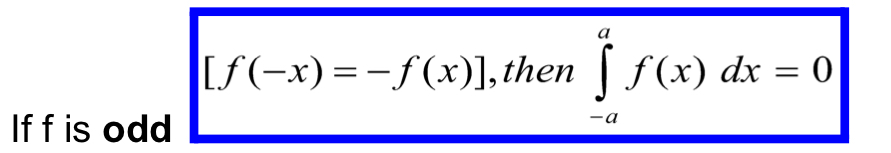
Integration Rules

Power, Log, Expo, Trig, Inverse Trig

Int Power Rule

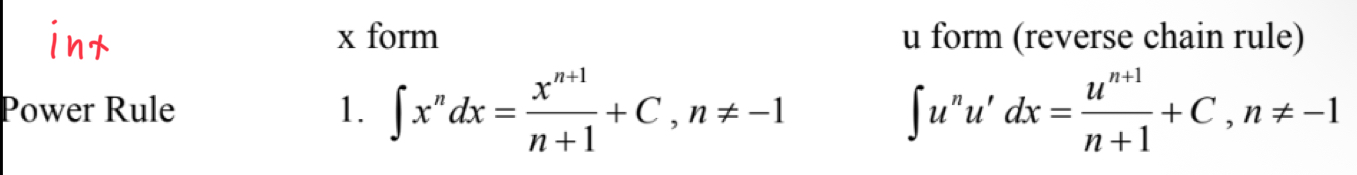
Int Log Rule

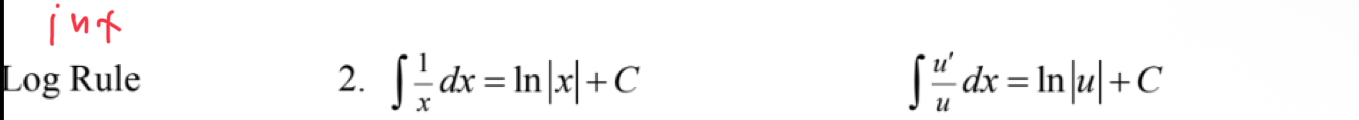
Int Expo Rule 1

Int Trig Rule 1

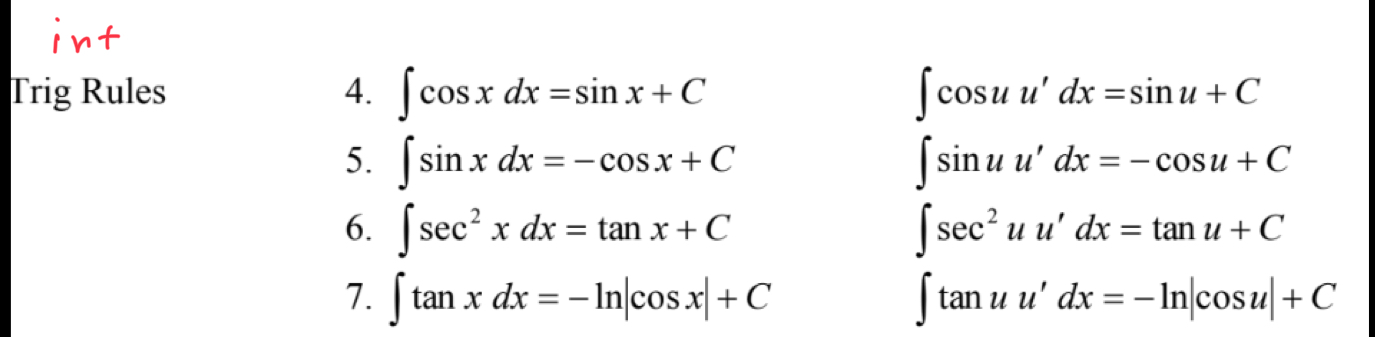
Int Inverse Trig Rule

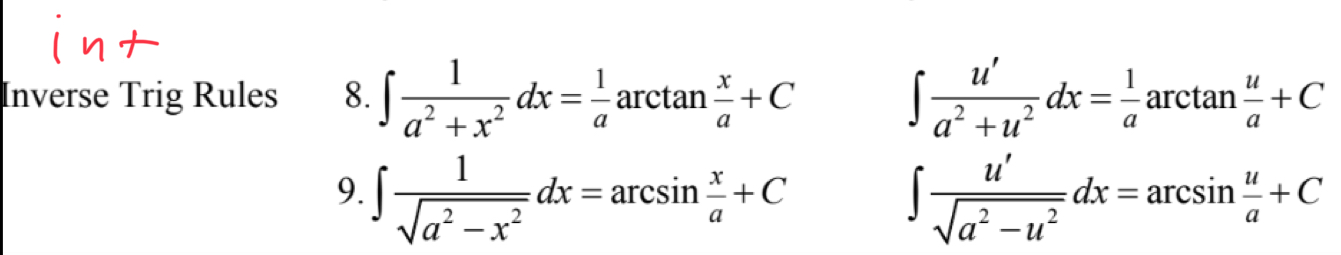
Int Trig rule 2

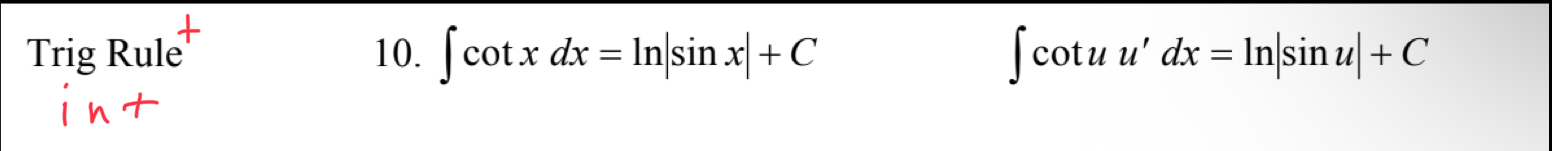
Int Expo Rule 2

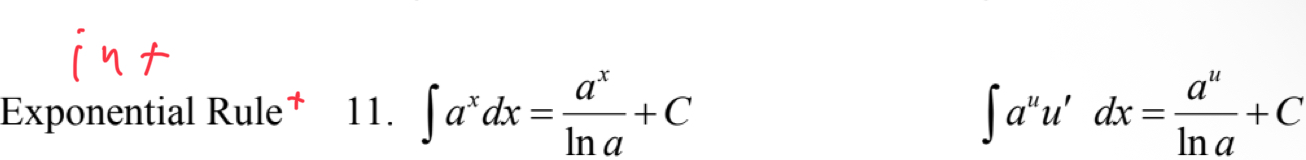
Int Trig Rule 3

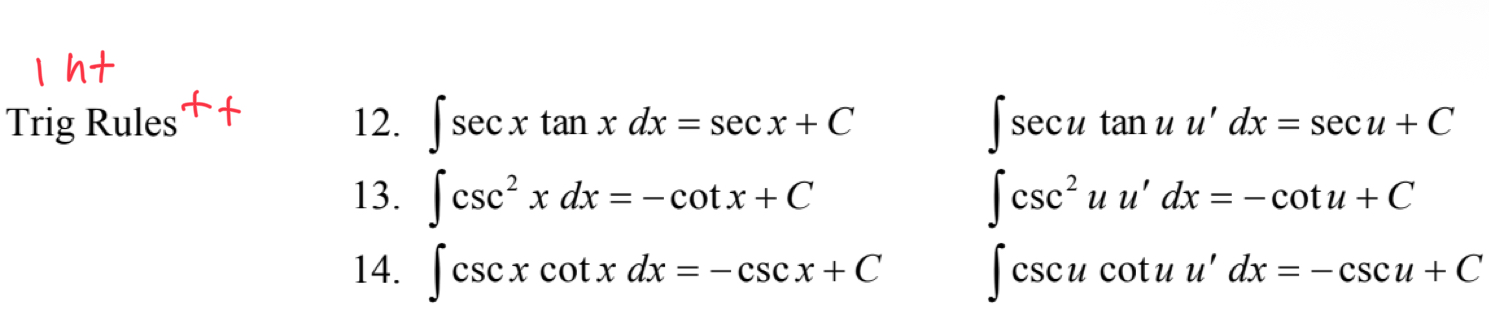
Special Integration Rule

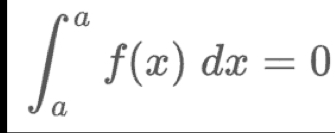
Fundamental Theorem of Calculus

Start plus Accumulation

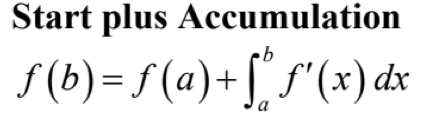
Slope or Direction Fields

1. If the segment along each vertical line have the same slope, the differential equation does not depend on y

2. If the segment along each horizontal line have the same slope, the differential equation does not depend on x

3. If the segments have positive slope, then there are likely no negatives in the expression from the derivative

4. If the slopes become larger as x increases, then y’ varies directly with x. Similarly for y

5. Otherwise, the derivative is inversely related to one or both variables

separate variables and integrate

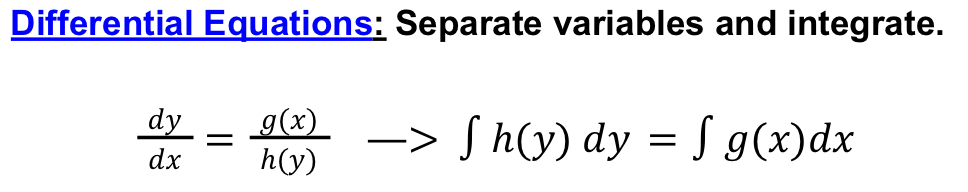
What does it mean when you are asked to optimize a function.

You find the abs min or max y evaluating the function at critical points and endpoints in the given interval.

Volume of a cylinder

V = πr²h

Volume of a cone

V = 1/3 * (πr²h)

Volume of a sphere

V = 4/3 * πr³

Volume of a Pyramid

V = 1/3 (L* w * h)

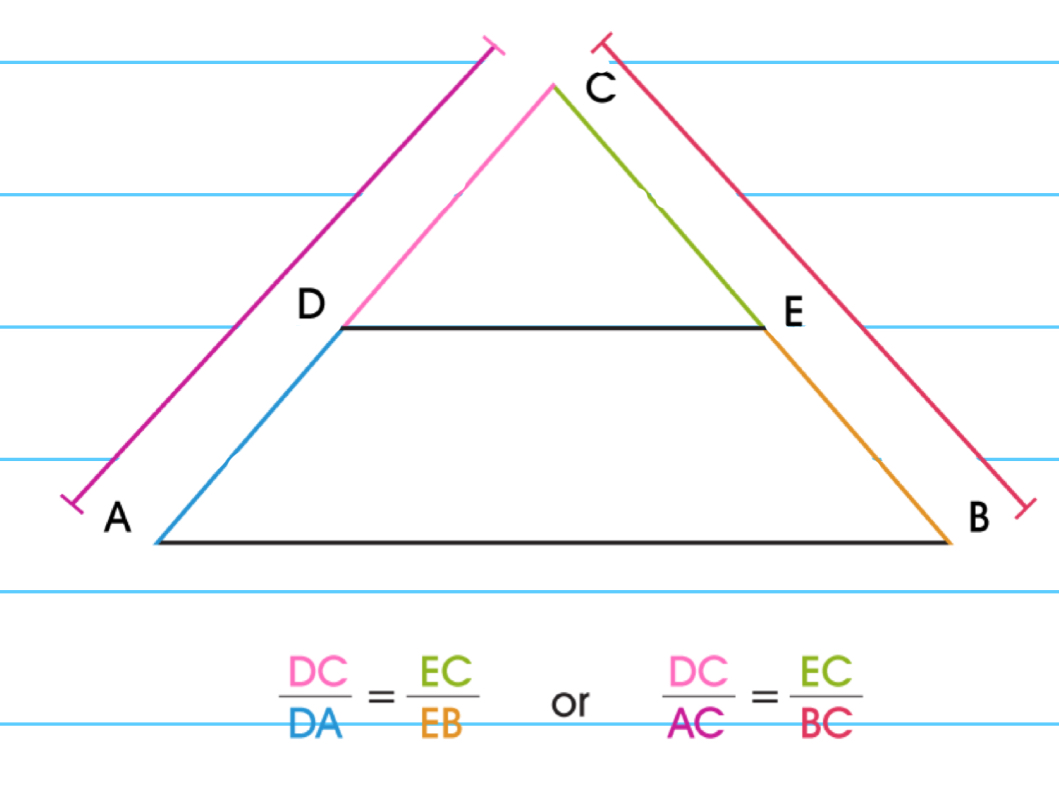
Similar triangle theorem

States that if two triangles have proportional corresponding sides, then they are similar and their corresponding angles are equal.