phys studying
0.0(0)
0.0(0)
Card Sorting
1/114
There's no tags or description
Looks like no tags are added yet.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
115 Terms
1
New cards
What is r21 and what is its magnitude r21?
\

2
New cards
What is the force vector F21 from m2 on m1?
F21 = G(6j-8k)kg^2/m^2
3
New cards
What is the force vector F12 from m1 on m2?
F12 = -F21 = G(-6j+8k)kg^2/m^2
4
New cards
What is the force vector on m1, Fnet1, due to m2 and m3?
Fnet1 = G(20i+6j-8k)
5
New cards
Calculate the net force on the 10 kg mass in the center of the \n equally spaced circle of sixteen 5 kg masses shown. The circle of masses is in the x-y plane and has a radius of 2 m.
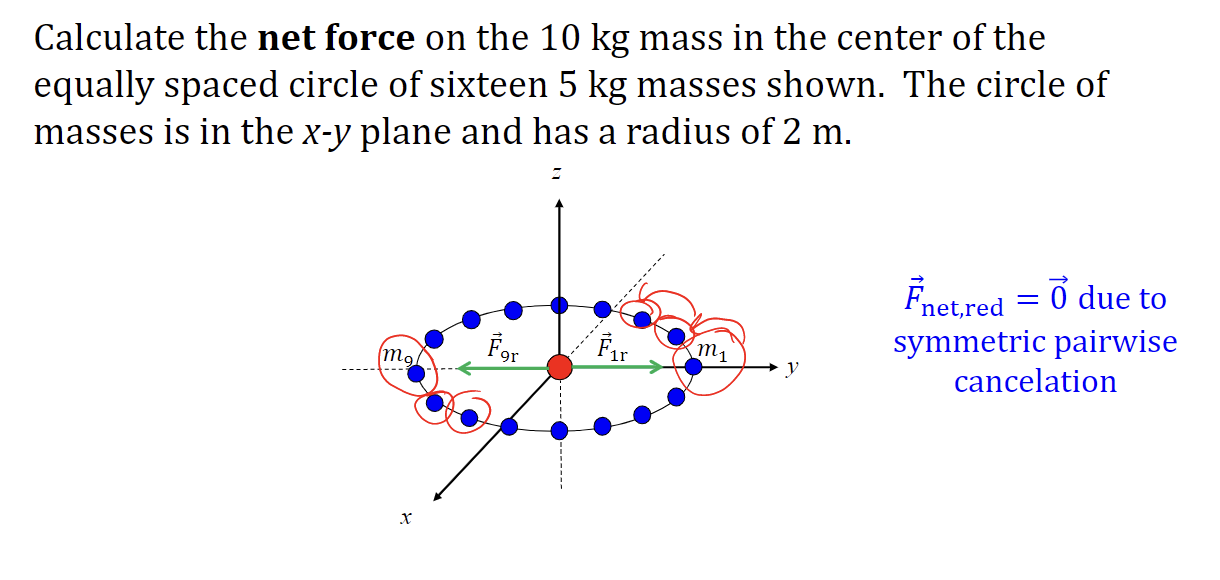
6
New cards
Is the net force on the 10 kg mass above the center of the equally spaced circle of sixteen 5 kg masses shown still zero?
No
7
New cards
The 2-D object shown below has mass density which varies as 𝜎 𝑥 = 𝜆𝑜(𝑎 − 𝑥). Which is the correct and most useful expression for 𝑑𝑚?
dm = 𝜆𝑜( 𝑎 − 𝑥 )𝑏/𝑎 𝑥𝑑𝑥
8
New cards
The 2-D object shown below is broken up into infinitesimal rectangles as shown. Which is the correct expression for 𝑑𝐼 about the y-axis?
𝑑𝐼 = 𝑑𝑚 𝑥^2
9
New cards
A particle b moves along the x-axis subject to a single conservative force that varies as Ԧ𝐹ab = (−𝐴 + 𝐵𝑥 + 𝐶𝑥^2) 𝑖, where 𝐴 = 1 N, 𝐵 = 1 N/m and 𝐶 = 1 N/m^2, and object a remains at rest. If b is released at 𝑥 = −1 m with 2 J of kinetic energy, determine its subsequent motion
It could move right or left at first, who knows...it’s a little spicy, but eventually it will move off to the right
10
New cards
A particle b moves along the x-axis subject to a single conservative force that varies as Ԧ𝐹ab = (−𝐴 + 𝐵𝑥 + 𝐶𝑥2) Ƹ𝑖, where 𝐴 = 1 N, 𝐵 = 1 N/m and 𝐶 = 1 N/m2, and object a remains at rest. If b is released at 𝑥 = 0 m with 1 J of kinetic energy, determine its kinetic energy when it reaches the point shown.
sys = a + b
𝑊tot = 0 → 𝐸sys,i = 𝐸sys,f
𝐾i + 𝑈i = 𝐾f + 𝑈f
𝐾i = 1 J, 𝑈i = 0 J → 𝐸sys = 1 J
1 J = 𝐾f + (−1 J)
𝐾f = 2 J
𝑊tot = 0 → 𝐸sys,i = 𝐸sys,f
𝐾i + 𝑈i = 𝐾f + 𝑈f
𝐾i = 1 J, 𝑈i = 0 J → 𝐸sys = 1 J
1 J = 𝐾f + (−1 J)
𝐾f = 2 J
11
New cards
Particle b starts from rest at point (i) and moves in the potential shown. Where will it have the largest speed and where will it have the largest magnitude of acceleration?
𝑣max at (ii) , 𝑎max at (i)
12
New cards
1\. They allow us to determine the total energy of a system, which is a useful physical quantity.
2\. They allow us to qualitatively describe the motion.
3\. They allow us to identify and characterize equilibrium positions.
4\. They allow us to do quantitative calculations that would otherwise be pretty hard
2\. They allow us to qualitatively describe the motion.
3\. They allow us to identify and characterize equilibrium positions.
4\. They allow us to do quantitative calculations that would otherwise be pretty hard
F,T,T,T
13
New cards
If Ԧ𝑣 is constant, the particle’s angular momentum at Position 1 (with respect to the point shown) is
the same as the particle’s angular momentum at Position 2.
14
New cards
Two objects of mass 50 kg move along parallel paths separated by 3m. Both objects have equal speeds of 2.0 m/s. What is the magnitude of the total angular momentum of the two-object system about a point that is in the middle of them?
300 kg\*m^2/s
15
New cards
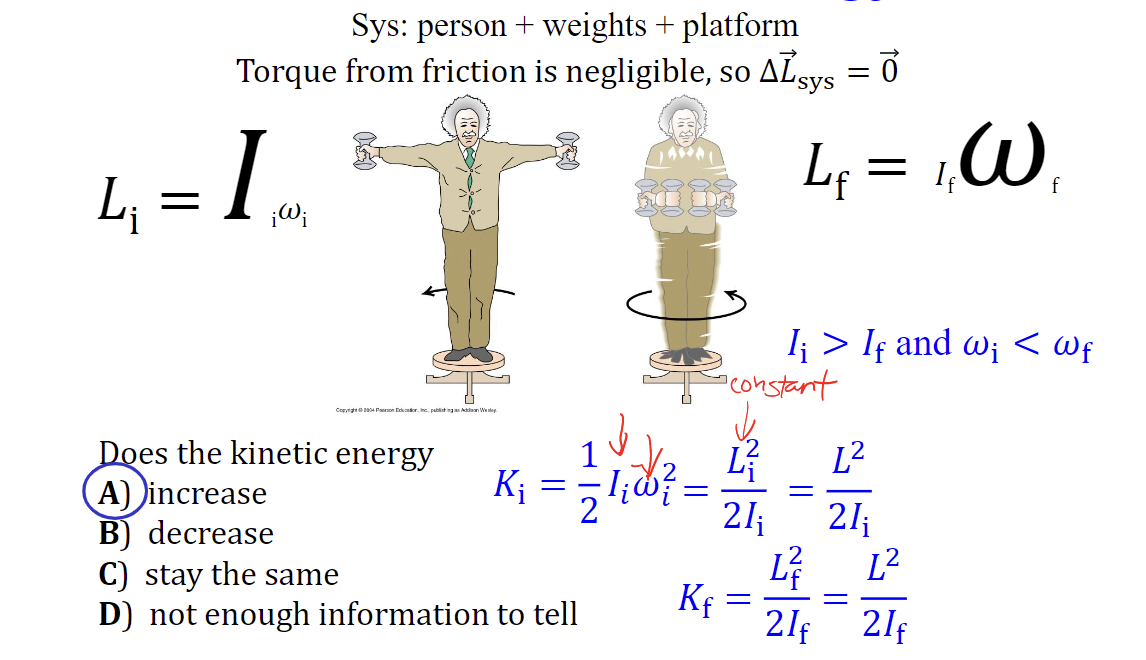
increase
16
New cards
If I stand on the platform with the wheel spinning clockwise (from above) and then flip the wheel over, what will happen?
I will rotate clockwise
17
New cards
A cue ball and an eight ball are on a pool table. The cue ball hits the eight ball and the two balls leave the collision as shown. If the initial time is just before the collision between the two balls, and the final time is just after, what is true about the eight ball’s linear momentum during this collision?
It is NOT constant
18
New cards
An elastic collision is one where the kinetic energy is (approximately) the same before and after the collision. Classify the following collisions as approximately elastic collision (EC) or an inelastic collision (IC) : \n 1. Two billiard balls colliding \n 2. A satellite “slingshot” around a planet \n 3. A car crash \n 4. An object “exploding” into three fragments
EC,EC,IC,IC
19
New cards
Elastic Collisions: (objects do not deform, microscopic, noncontact and idealized scenarios)
Kinetic energy IS constant
20
New cards
Inelastic Collisions: (objects typically deform, most macroscopic collisions)
Kinetic energy is NOT constant
21
New cards
Two objects of equal mass collide as shown. If 𝑣1i = 3 m/s, 𝑣2i = 4 m/s and 𝑣1f = 5 m/s, is the collision elastic?
Yes
22
New cards
A bowling ball and a golf ball are both purely translating with the same (nonzero) momentum. Which has the larger kinetic energy?
The golf ball
23
New cards
A bowling ball and a golf ball are both purely translating with the same initial (nonzero) momentum. If you exert the same constant force on each (in the opposite direction of the motion), which takes more time to stop?
It takes the same time
24
New cards
A bowling ball and a golf ball are both purely translating with the same initial (nonzero) momentum. If you exert the same constant force on each (in the opposite direction of the motion), which travels further before stopping?
The golf ball
25
New cards
A normal bullet and a rubber bullet of the same mass are fired at log. Both hit the log with the same initial momentum. The normal bullet lodges itself inside the log, while the rubber bullet bounces off. If the time interval for stopping the normal bullet and reversing the rubber bullet are the same, which one is more likely to knock over the log? Hint: Which one corresponds to a greater average force?
The rubber bullet
26
New cards
A platform (p) moves upwards as shown. Initially two objects on it are connected by a compressed spring and then released. The final configuration is just when the spring reaches it uncompressed length. The block (b) slides with kinetic friction and the cylinder (c) rolls without slipping. WEb gives rise to a
Negative work done on the system
27
New cards
A platform (p) moves upwards as shown. Initially two objects on it are connected by a compressed spring and then released. The final configuration is just when the spring reaches it uncompressed length. The block (b) slides with kinetic friction and the cylinder (c) rolls without slipping. Fsp,bc gives rise to a
Negative change in PE
28
New cards
A platform (p) moves upwards as shown. Initially two objects on it are connected by a compressed spring and then released. The final configuration is just when the spring reaches it uncompressed length. The block (b) slides with kinetic friction and the cylinder (c) rolls without slipping. fk,pb gives rise to a
None of these
29
New cards
If 𝑚R >> 𝑚Y, which of the terms is approximately zero?
More than one (A&C)
30
New cards
If both objects start at rest and have equal mass, do the two integrals cancel for the combined isolated system?
No
31
New cards
A constant force 𝐹YC is applied to two identical cylinders that start from rest and (1) rotates about a fixed, low-friction axle, and (2) rolls without slipping on a horizontal surface. After one full revolution, which cylinder has the larger change in (total) kinetic energy?
The change in the total KE is the same
32
New cards
A 5-kg book slides across a table with an initial kinetic energy of 10 J. If kinetic friction between the table and the book (μk = 0.204) causes the book to stop after 1 m, how much work does the kinetic friction force do on the book?
Unable to be determined
33
New cards
The values for energies/work depend on the choice of “observer”.
Both external and internal forces can do work.
The total energy of a system is always constant.
Energy is a conserved quantity.
Both external and internal forces can do work.
The total energy of a system is always constant.
Energy is a conserved quantity.
T,F,F,T
34
New cards
A baby is doing push-ups on a level floor. He has a 7-kg mass and pushes his body from 5 cm above the floor to 20 cm above the floor. The work done on the baby by the normal force of the floor on the baby is:
equal to zero
35
New cards
What is the work done by gravity on the block?
mb\*g(sin(theta))d
36
New cards
What is the work done by the normal force on the block?
WNRb = 0
37
New cards
What is the final speed of the block?
𝑣f =sqrt( 2𝑔 (sin 𝜃) 𝑑)
38
New cards
A solid spherical ball starts from rest and rolls without slipping down an inclined plane. Which direction is the friction force on the ball?
up the plane
39
New cards
You are going to race two hoops down an incline plane. Hoop 1 is larger and heavier than Hoop 2, with 𝑅1 = 2𝑅2 and 𝑚1 = 2𝑚2. Which one reaches the bottom first?
They tie
40
New cards
If the double-radius cylinder rolls without slipping on the table under the applied force shown, which way will its COM accelerate? Note that G = ground.
To the left
41
New cards
A large cylinder (r = r2) is welded to two smaller cylinders (r = r1) that act as an axle. If the small cylinders roll without slipping on the metal rods (R) under the applied force shown, which way will the large cylinder’s COM accelerate?
To the right
42
New cards
Starting from rest, if the cylinder rolls without slipping on the table under the applied force shown, which way will its center of mass (COM) accelerate?
It can’t roll without slipping!
43
New cards
If a physical pulley (p) is rotating about an axle with negligible friction with the angular acceleration shown, what must be true about the tension forces?
𝑇1p > 𝑇2p
44
New cards
For which axis would there be the fewest nonzero torques on the system of the pickaxe?
A (the one in space to the left)

45
New cards
You want to find the force of static friction from the floor on the pickaxe in the fastest way possible. That is, with the fewest number of equations (N2L in x, y, and for rotation). What is the fewest number of equations you could use? Assume you know the mass of the pickaxe and all relevant distances.
1
46
New cards
A block of mass mb hangs from a cable that is attached to the end of a uniform strut of length L and mass ms. The strut is pinned at one end and also joined to the ground by a rope attached a distance d from the pin as shown. Find the tension in the rope between the ground to the strut.
𝑇gs =(𝐿𝑔 sin 𝜙 (1/2 𝑚s + 𝑚b))/(𝑑 sin 𝜃)
47
New cards
A block with mass mb hangs from a string that is wrapped around a physical pulley with radius Rp and moment of inertia Ip. The pulley can rotate about an axle (a) with negligible friction
Less than mb\*g
48
New cards

A beam rests on the ground and is stabilized by two taut ropes attached as shown. Note that the angles are the same
τ1b = τ2b
49
New cards
In general when an extended object rotates, which type of acceleration is the same for each small piece of which it is made?
None of these
50
New cards
How do the moments of inertia of the sledgehammer about the indicated axes of rotation compare?
I1 < I2 < I3
51
New cards
Which is true?
A)For a given force there is one \n possible torque. \n B) If the net force on a system is \n zero, then the net torque is zero. \n C) If the net torque on a system is \n zero, then the net force is zero. \n D) If the torque is zero, then the \n associated force is zero. \n E) None of the above
A)For a given force there is one \n possible torque. \n B) If the net force on a system is \n zero, then the net torque is zero. \n C) If the net torque on a system is \n zero, then the net force is zero. \n D) If the torque is zero, then the \n associated force is zero. \n E) None of the above
None of the above
52
New cards
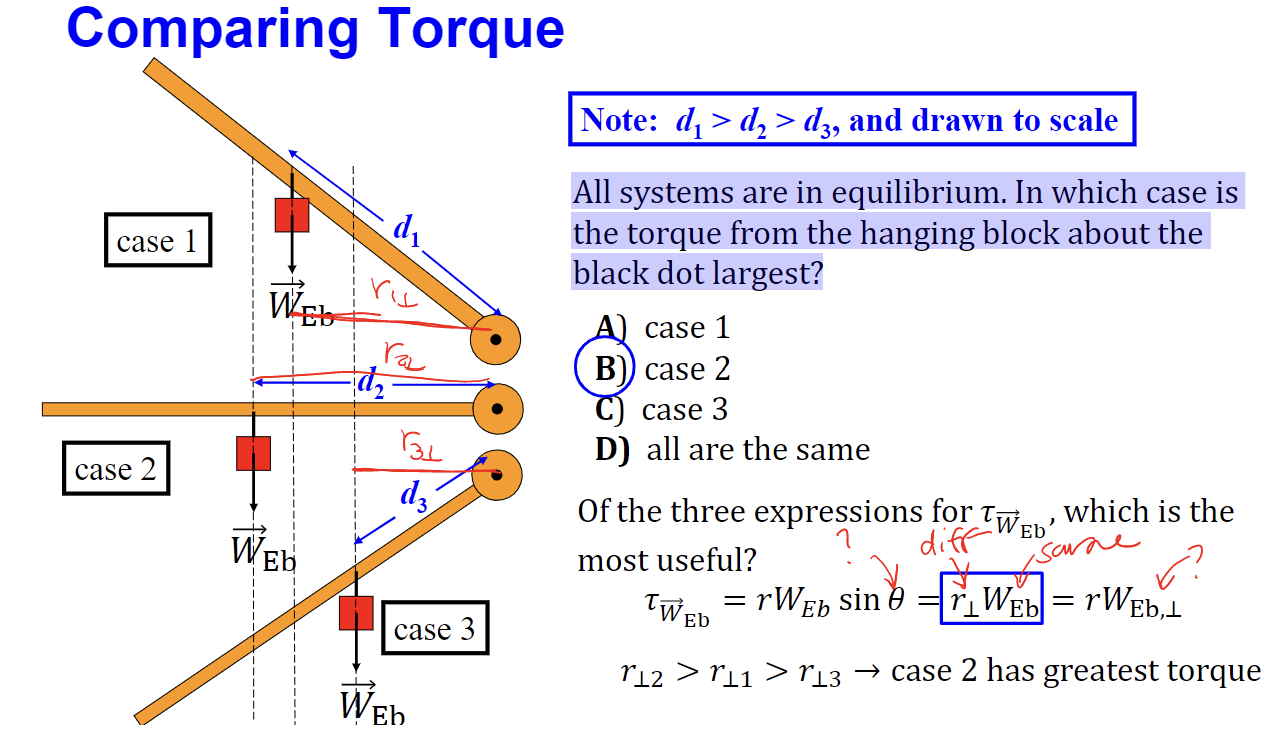
All systems are in equilibrium. In which case is the torque from the hanging block about the black dot largest?
case 2
53
New cards
Block (B) is at rest on the inclined plane (P). This implies that σ𝑗 Ԧ𝜏𝑗𝐵 = 0 about any axis. Which EFBD below has the normal force in the correct location?

54
New cards
Determine the direction of 𝑉1 × 𝑉2 and 𝑉2 × 𝑉1
\-z, +z
55
New cards
What do you get when you perform the following operations in \n a right-handed coordinate system:
i and -j
56
New cards
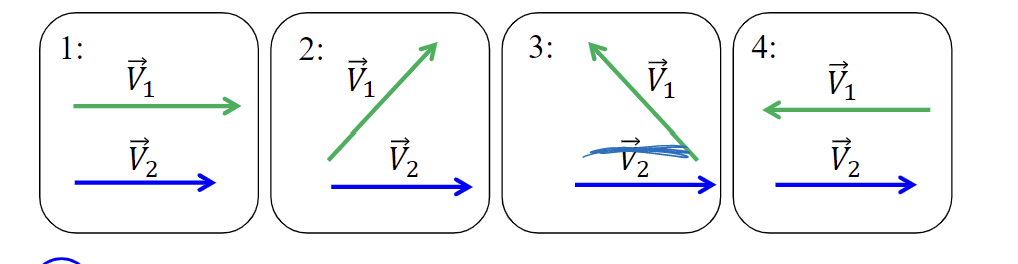
Rank the following dot products of 𝑉1 ∙ 𝑉2 from most positive to most negative. (Note that the magnitudes of 𝑉1 and 𝑉2 do not change.)
1>2>3>4
57
New cards
Which of the following mathematical statements don’t make sense?
𝑉1 + (𝑉2∙ 𝑉3)
58
New cards
A book (b) is sitting on the ground, and you pick it up and put it on a table as shown. For this process, calculate the following (called a line integral):
−𝑚b𝑔(𝑦f − 𝑦i)
59
New cards
Four masses are each acted upon by a net external force SFx that depends on the position x of the mass according to the graphs below. Which one will NOT oscillate?
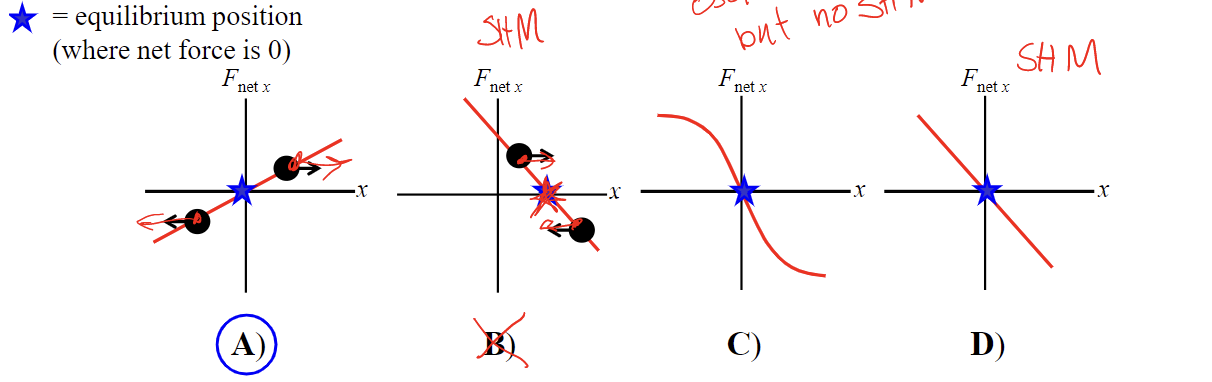
60
New cards
An ideal bouncy ball bounces off an ideally rigid surface so that it always reaches the same height on each bounce. Is the ball undergoing SHM?
No
61
New cards
A block attached to a spring undergoes SHM. The graph shows the velocity of the mass as a function of time. Which of the following expressions is equal to the amplitude of the position of the block?
𝑣max/𝜔
62
New cards
A block is hanging at rest from a vertical spring. Use a coordinate system with the y-axis pointing vertically up, the mass is in mechanical equilibrium at y = 0. You pull the mass down from the equilibrium position and give it an initial velocity down at t = 0. Select the set of graphs that could represent y(t), vy(t), and ay(t) for the block.
y = iii; vy = i; ay = iv
63
New cards
Blaster is attached to two fixed walls by springs and slides with negligible friction on the table. Both springs remain stretched throughout the motion and have different spring constants. What is the angular frequency of oscillation of Blaster?
𝜔 = sqrt((𝑘1+𝑘2) /(𝑚B))
64
New cards
If the red object is moving clockwise around the circular path at constant speed, what directions are the centripetal and tangential components of its acceleration at the position shown?
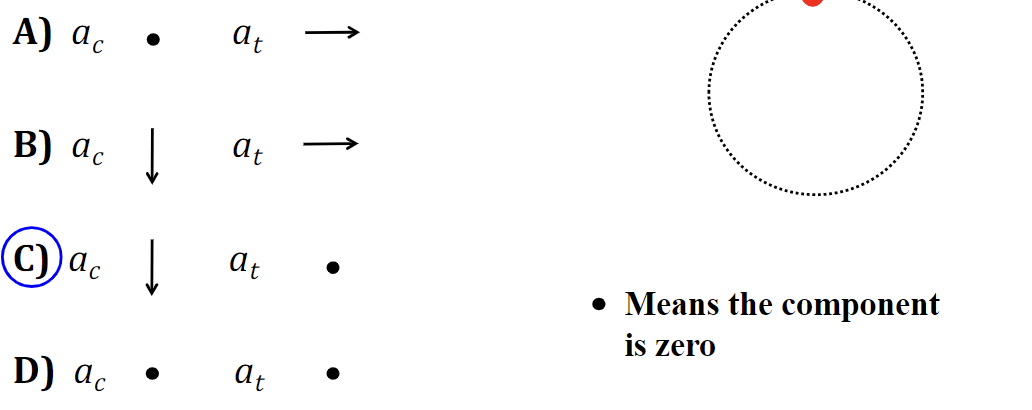
65
New cards
You roll a bowling ball across a floor. How do you have to continuously tap it to get it to move in a circle at constant speed?
Perpendicular to the direction it’s rolling
66
New cards
Which of FBDs below is most accurate for a wagon with ideal wheels (negligible friction) and Blaster rolling through the bottom of a dip?
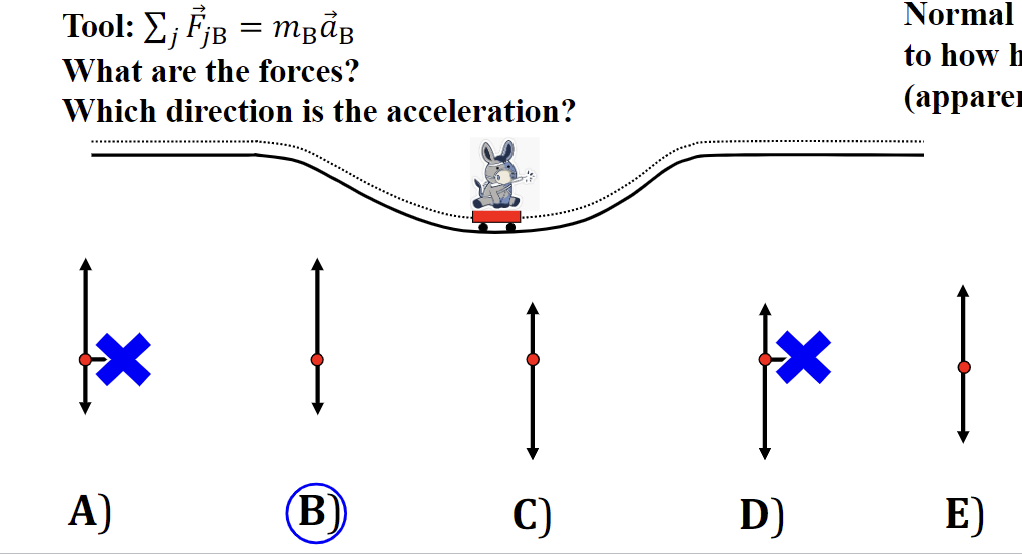
67
New cards
A motorcyclist is rounding a flat curve at a constant speed 𝑣. She is more likely to slip if she rides along the
inside edge of the curve
68
New cards
In what direction does the static friction force 𝑓s,BC from the block on the cart point?
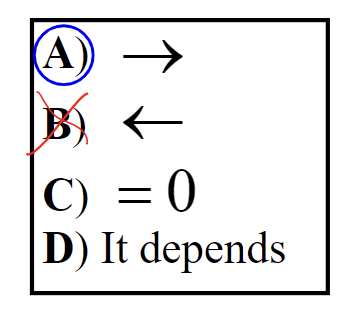
69
New cards
How does the magnitude of the static friction force fs,CB between the cart and the block relate to FYB, the magnitude of your pushing force? Again, the block does not slip across the cart
fs,CB < FYB
70
New cards
Suppose you were given the previous problem and provided with the following possible solutions. Determine which one could be correct
𝑇2B = ((2𝑇1B − (𝑚B𝑔)/ (sin 𝜃)) cos 𝜃)/𝑚B
71
New cards
Suppose you were given the problem on the previous slide and provided with the following possible solutions for TTB. Which one could be correct?
𝑇TB = 𝑚B𝑔/ cos 𝜃
72
New cards
The importance of Newton’s first law is best indicated in which statement?
Newton’s first law helps indicate when we are allowed to use Newton’s second law
73
New cards
You pull on a block as shown, but the block does not slip. If the magnitude FYb of your force is unchanged, but the angle q is increased, how does the magnitude of the friction force from the table on the block change?
It decreases
74
New cards
The kinetic friction force on an object always \n opposes the motion of the object
False
75
New cards
Static friction cannot cause objects to accelerate.
False
76
New cards
An object can be pushed by an external force with magnitude larger than UsNab and not slip
True
77
New cards
Blaster (“B”) is sitting in a cage (“C”). The cage is sitting on a table and is at rest. The Newton’s 3rd Law pair to the normal force of the cage on Blaster is
the normal force of Blaster on the cage
78
New cards
Blaster is sitting in a cage. The cage is sitting on a table and is at rest. The magnitude of the normal force from the cage on Blaster is the same as the magnitude of Blaster's weight because
of Newton’s 2nd law
79
New cards
Blaster, with a mass of 200 kg, is now sitting in a cage in an \n elevator that is going down and slowing down, with an \n acceleration of magnitude 2.0 m/s2. Find the magnitude and \n direction of the force from Blaster on the cage.
𝑁BC = −2362 N 𝑗
80
New cards
Blaster, with a mass of 200 kg, is now sitting in a cage in an elevator that is going down and slowing down. In which direction is Blaster accelerating relative to 1) Blaster in the cage and 2) a person standing on the ground?
0, up
81
New cards
A car undergoes an acceleration 𝑎𝑥 𝑡 from 𝑡1 to 𝑡2. Given 𝑣𝑥 𝑡1 and 𝑥 𝑡1 , what is the correct expression for 𝑥 𝑡2 ?
\

82
New cards
Given the velocity graph shown, which is true about 𝑣av 𝑥, 𝑎av 𝑥, and Δ𝑥 from 𝑡 = 𝑡i to 𝑡 = 𝑡f?
𝑣av 𝑥 < 0 𝑎av 𝑥 > 0 Δ𝑥 < 0
83
New cards
A car makes one lap around a track at constant speed 𝑣𝑜 in a time T. Over the time it takes to go one lap, how do the magnitude of its average velocity and average speed compare?
magnitude of average velocity < average speed
84
New cards
Two bullets start at the same height. One is fired horizontally from a gun, and the other is dropped from rest. Which hits the ground first?
Neither
85
New cards
Four identical baseballs are thrown across a baseball field with the same initial speed, but they are tossed at different launch angles 𝜃. Air resistance is negligible along each trajectory. Rank the paths according to the time the baseball is in the air.
D < C < B < A
86
New cards
What effect will taking a step closer to the window have on the balloon’s impact speed (𝑣f ) at the house?
It depends
87
New cards
Which of the following physical quantities could not be described by a vector?
Mass
88
New cards
For the vectors shown which of the following is true about 𝑉3 = 𝑉1+𝑉2?
None of the above are correct
89
New cards
For the vectors shown which of the following is true about 𝑉3 = 𝑉1+𝑉2?
𝑉3 < 𝑉1+𝑉2
90
New cards
For the vectors shown which of the following is true about 𝑉4 = 𝑉1 − 𝑉2?
𝑉4𝑥 > 0; 𝑉4𝑦> 0
91
New cards
For the vectors shown which of the following is true about 𝑉5 = −𝑉1+𝑉2?
𝑉5 = 7 sqrt(2)
92
New cards
What does the speed tell you about the motion of an object?
How fast it is going
93
New cards
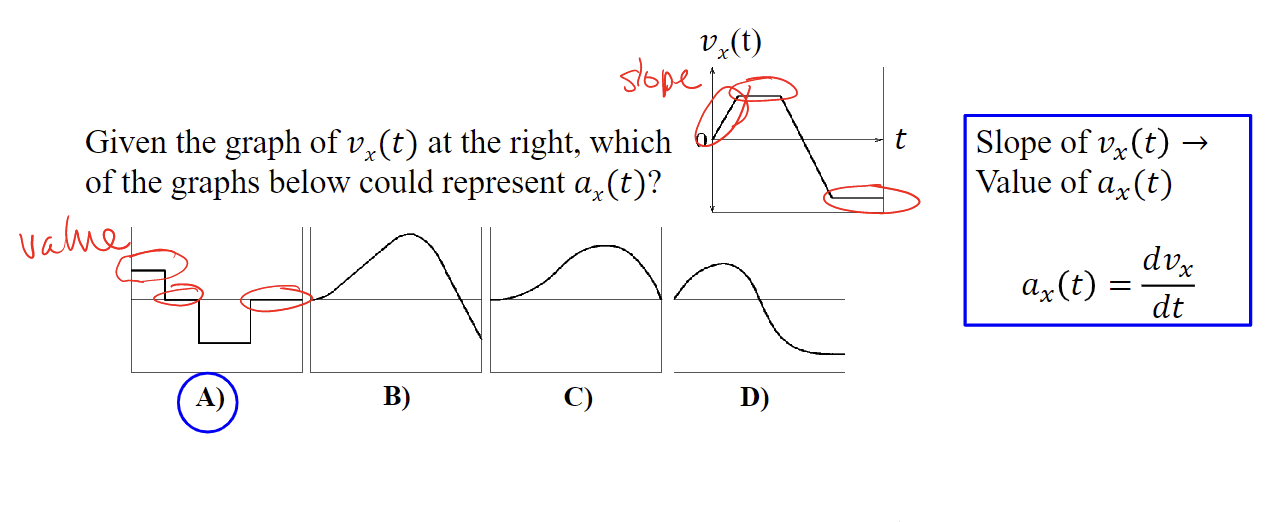
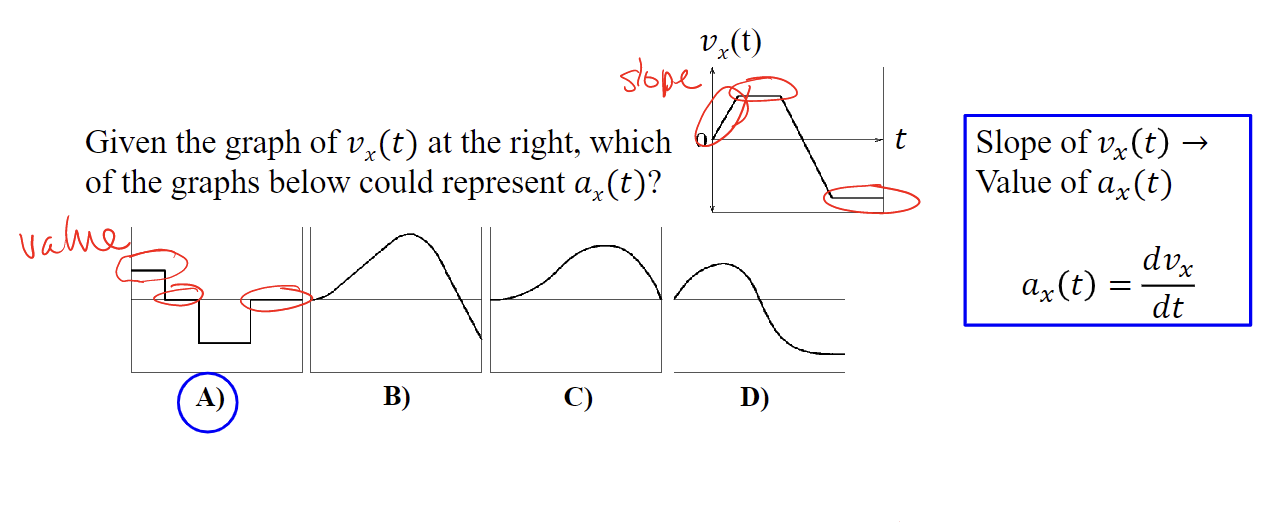
94
New cards
Given the graph of 𝑣𝑥(𝑡) at the right, during which segments is the object speeding up?
1, 4
95
New cards
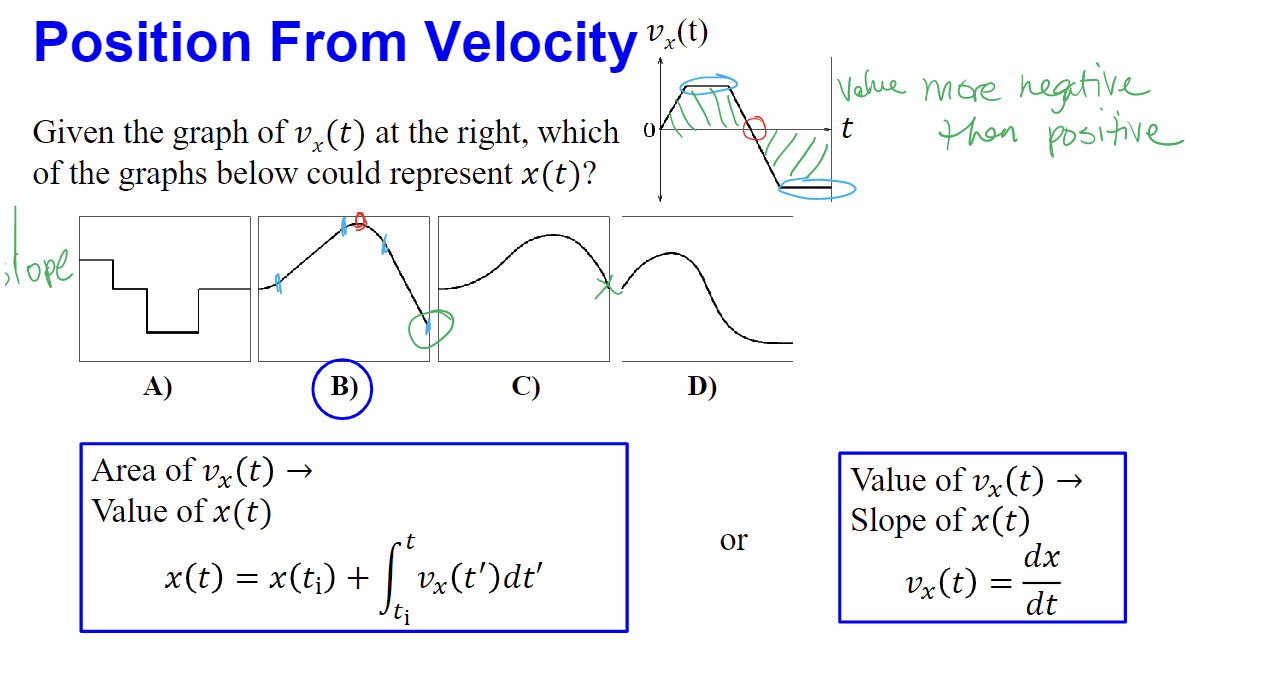
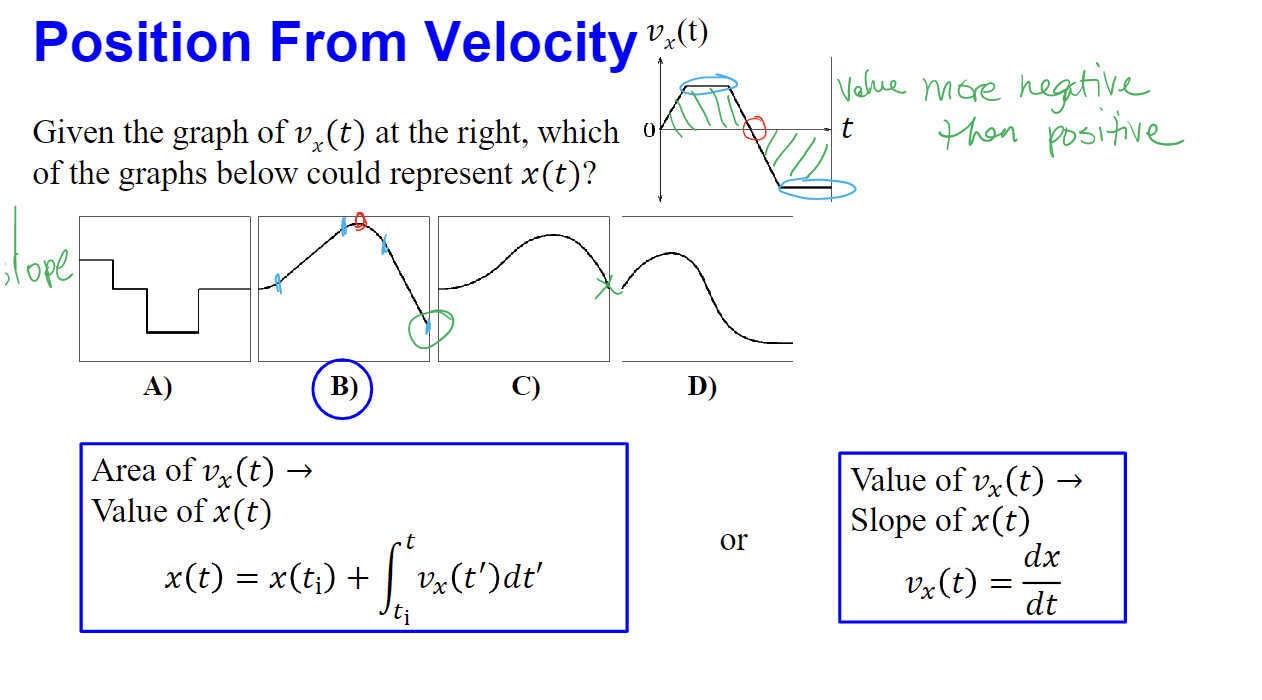
96
New cards
In an experiment to determine the viscosity of some oil, a ball is dropped into the oil. The position of the ball is given by the formula 𝑦(𝑡) = 𝐴 + 𝐵𝑡 + 𝐶𝑒−𝐷𝑡, where 𝑦 is given in meters, and 𝑡 is the time in seconds. At 𝑡 = 0, 𝑦(0) = 0.07 m, the 𝑦-component of the velocity is zero and the 𝑦-component of the acceleration is 0.03 m/s2. As 𝑡 approaches infinity, the 𝑦-component of the velocity approaches 𝑣(∞) = 0.45 m/s. What is the value of 𝐵?
0\.45 m/s
97
New cards
A motorcyclist starts at rest at 𝑡 = 0 and then moves along a straight line. Her acceleration is 𝑎𝑥(𝑡) = 𝐴 − 𝐵𝑡 until time 𝑡1. After the time 𝑡1, the acceleration drops to 0, and she continues at a constant velocity until time 𝑡2. What is 𝑣𝑥(𝑡2), that is, her x component of velocity at time 𝑡2?
𝐴𝑡1 − 1/2 𝐵𝑡1^2
98
New cards
The velocity as a function of time for an asteroid in the asteroid belt is given by: 𝑣 (𝑡) = 𝐴𝑡𝑖̂ + 𝐵𝑡2𝑗̂ Where 𝐴 and 𝐵 are constants. If 𝑡i = 0 is the initial time and 𝑡f is the final time, what is the magnitude of the average acceleration of the asteroid over this time period?
√(𝐴)^2 + (𝐵𝑡f)^2
99
New cards
When “pinching” a rock while rock climbing (like we discussed in Studio), which of the following statements are true?
I. Being able to squeeze the rock harder increases the force of static friction between your hand and the rock.
II. Being able to squeeze the rock harder increases the maximum force that static friction can have between your hand and the rock.
I. Being able to squeeze the rock harder increases the force of static friction between your hand and the rock.
II. Being able to squeeze the rock harder increases the maximum force that static friction can have between your hand and the rock.
I is false, II is true
100
New cards
Block 1 (with 𝑚1 = 2.0 kg) sits on top of Block 2 (with 𝑚2 = 8.0 kg) under the influence of a force of magnitude 17 N applied horizontally to Block 1 as shown. The coefficient of static friction between the two blocks is 0.50 and friction between Block 2 and the floor is negligible. Does the upper block slip with respect to the lower block and why?
Yes, because 𝑓s,12 > 𝑓s,12 max