ai part 2

minimum remaining values heuristic

choose successor with the fewest legal values, selects successor states that are more likely to result in failure

degree heuristic

choose successor involved with the largest number of constraints on other potential successors

least constraining value

given a variable, assign the value that makes the fewest choices of variables for neighbouring candidates.

variables vs values (example: states and colour)

Variable

An unknown that must be assigned a value.

Value

A possible option from the domain that can be assigned to a variable.

WA, NT, SA

Variables

These are the regions that need a color assigned.

{Red, Green, Blue}

Values

These are the possible colors you can assign to each variable (region).

If the task is to schedule classes into time slots

variables = classes. and domain = available time slots or rooms

Explain why it is a good heuristic to choose the variable that is most

constrained but the value that is least constraining in a CSP search.

The search tree for solutions grows exponentially, but most branches are invalid combi-

nations of assignments.

• The Minimum Remaining Values (MRV) heuristic chooses the variable most likely to

cause a failure - if search fails early, backtrack and prune the search space. If the current

partial solution cannot be expanded into a complete solution, is it better to know earlier

instead of wasting time searching exponentially many dead-ends.

• Because we need to find a single solution, we want to be generous and select the value

that allows the most future assignments to avoid conflict. This makes it more likely the

search will find a complete solution.

• This asymmetry makes it better to use MRV to prune exponentially growing search space

by choosing least-promising successors first, but increase the probability of success for

all successors via the least constraining value heuristic.

what is forward checking

Keep track of remaining legal values for unassigned variables

Terminate search when any variable has no legal values

what is a tree structured CSP

A tree-structured CSP has no loops in the constraint graph

explain ac-3 on a tree structured csp and give

A tree-structured CSP has no loops in the constraint graph. We first choose an arbitrary

node to serve as the root, convert all undirected edges to directed edges pointing away

from the root, and then topologically sort the resulting directed acyclic graph using the

methods you learnt in Week 3.

• Make the resulting graph directed arc-consistent by performing a backward pass from

the tail to the root, enforcing arc consistency for all arcs Parent(Xi) →Xi. This will

prune the domain of the variables in the constraint graph. Throw a failure value if this

is not possible.

• Now start at the root, and perform a forward assignment using standard backtracking.

• Checking consistency requires O(D2) operations (pairwise comparison), and no arc must

be considered more than once in the absence of backtracking, for a worst-case runtime

of O(ED^2)

P (H|X, Y )

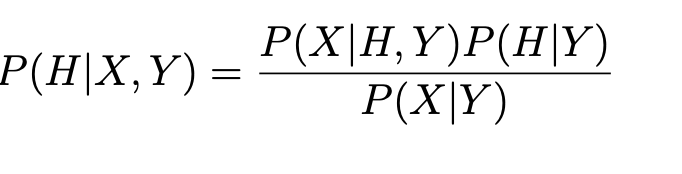
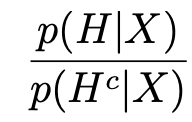
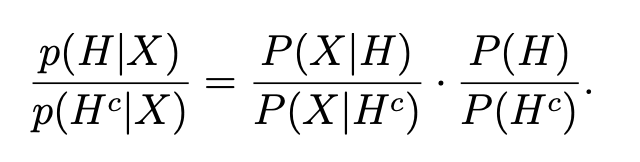
how to get posterior probability from posterior ratio

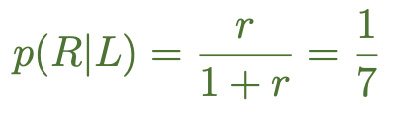
P (X|e)

P (H|X, Y )

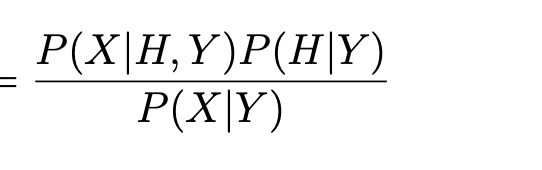
what is P(B,E) and what is P(X∣e)

P(B,E) is joint probability, P(X∣e) is conditional probability

how to find if two nodes are indepdent

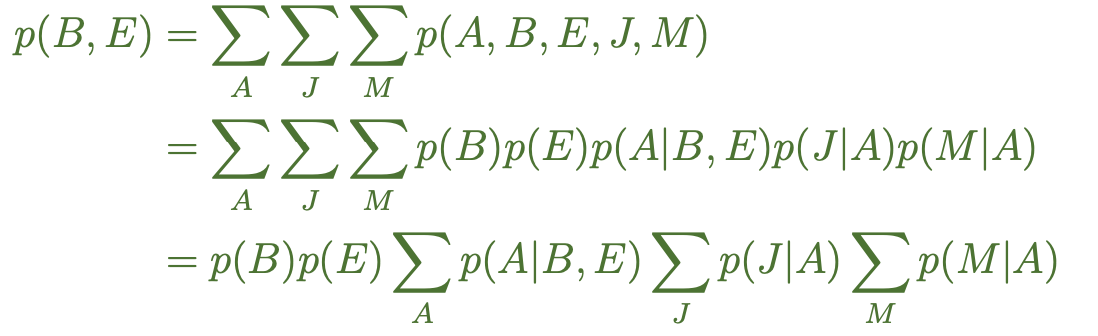
what is Expected Utility

Expected Utility of an action is the sum of the utilities of all possible outcomes, weighted

by their probabilities.

A Decision Network

is a directed acyclic graph (DAG) with chance nodes, decision nodes, and

utility nodes. The edges represent the dependencies between the nodes, similar to a Bayesian

network. The chance nodes represent the uncertain variables that affect the outcome of the decision.

The decision nodes represent the decisions that can be made, each with a set of possible actions.

The utility node represents the utility of the outcome based on the values of the chance nodes and

the decision nodes

do bayes nets have to be DAGs

yes

what is joint distribution

If you have two variables, say:

• AAA: whether it's raining (True or False)

• BBB: whether the ground is wet (True or False)

Then the joint distribution is:

P(A,B)P(A, B)P(A,B)

This gives the probabilities for every possible combination of values for AAA and BBB:

A	B	P(A, B)
True	True	0.3
True	False	0.1
False	True	0.4
False	False	0.2

shapes for decision networks

• Chance nodes (ovals): represent uncertainty

• Decision nodes (rectangles): represent choices

• Utility nodes (diamonds): represent preferences

p(H|xt+1)