Thermal physics

Internal energy definition

sum of the randomly distributed kinetic energies and potential energy of the particles in a body.

Key definitions

Particles have random kinetic energy due to random vibrations.

An object has potential energy stored in the bonds between particles.

In an object, the particles have a range of different energies.

Heat

the flow of energy from a higher temperature region to a lower temperature region.

Internal energy of one object decreases

Internal energy of other object(e.g.surroundings) increases

Temperature

The measure of the average random KE of the particles within an object.

How can the internal energy of a system change?

When energy is transferred to it by heating and when work is don't on it.

AND vice versa

Specific Heat Capacity

The heat required to raise the temperature of 1kg of an object by 1°C, without changing state.

ΔQ = mcΔθ

Δθ = change in temperature

c = specific heat capacity

m = mass of the object

q = energy required to increase temp by Δθ Celsius/kelvin

Δθ can be Celsius or kelvin

How to go from kelvin to Celsius

0 kelvin = -273 degrees Celsius

-273

Equilibrium Method

Used when one object is added to another object of different temperature, and there's a different resulting temperature.

Hot object - Temp decreases - (Initial - Final) = Δθ

Cold object - Temp increases - (Final - Initial) = Δθ

use SHC of hot = SHC of cold

SHC rate equations

P = (m/t) x cθ

P = mc x (θ/t)

P = power

m = mass

c = SHC

t = time (seconds)

θ = temp

Heating curve

Where there's a gradient = energy supplied to random KE of particles

where gradient = 0, energy used to break bonds

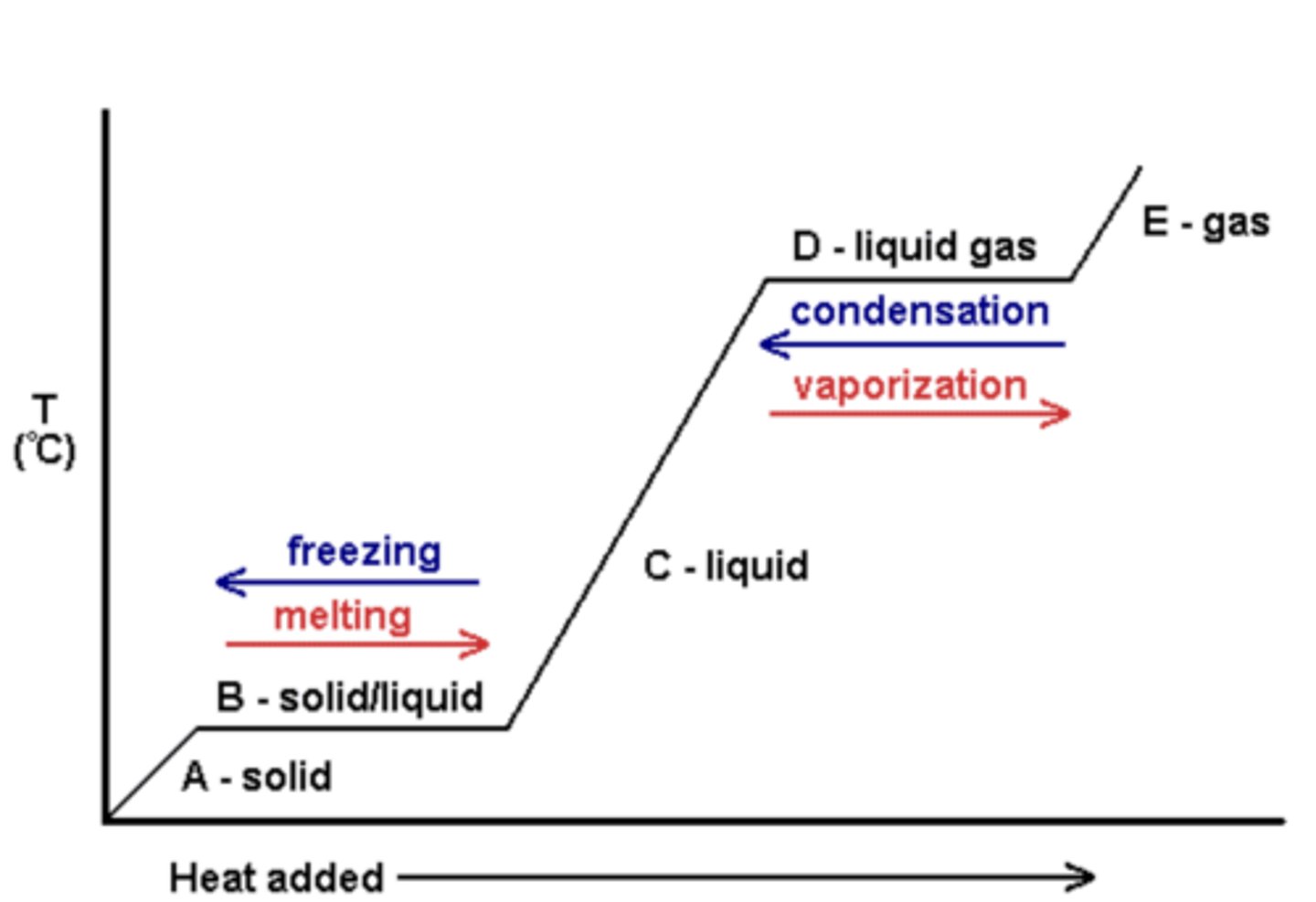
Heating curve NTK

ΔQ = mcΔθ

1/mc = Q/θ, 1/mc = gradient

gradient inversely proportional to SHC.

So if part of graph is steeper, SHC must be less.

For area of vaporisation or melting- energy is used to break bonds.

if one part is longer, the energy to boil/mass is greater

Latent Heat Experiment

Set up two funnels both with 50g of crushed ice.

Beakers underneath both.

put an immersion heater in one and turn it on(will know energy supplied).

measure mass of water in each beaker.

One is a control beaker - how much ice melts due to temperature of the room.

One is due to immersion heater and room.

(ih + r) - (r) = melted ice due to immersion heater

q = Δm x Latent heat

latent heat = energy supplied/mass of water(melted due to immersion heater)

Precautions taken for Latent Heat Experiment

ice crushed into small pieces + immersion heater fully submerged = all of heater is in contact with the ice. Any of the heater not in contact with ice, will heat air, energy dissipated to surroundings.

Using the control set up - finds mass of ice melted due to room temperature.

Latent Heat Formula

Energy = Δm x Latent heat

If a question is asked about how much energy to melt ... from ...

If temp isn't at melting/boiling point.

using SHC formula , Q=mcΔT until melting point

THEN use latent heat formula to find energy needed to melt it.

Latent Heat Definition

The energy required to melt 1kg of a substance, without raising its temperature.

Units for latent heat and specific heat capacity

latent heat = Joules/Kg

Specific heat capacity = Joules/kg(C/K)

SHC and Latent Heat of Ice and Water

SHC of Ice = 2030

SHC of Water = 4200

Latent heat of ice-water = 334000

Assumptions of Kinetic Theory

All collisions are elastic

there is a large number of particles

motions of particles is random

classical laws of physics apply

particles are identical

volume of gas > volume of particles

time of collisions < time between collisions

no external forces on the particles(except gravity)

no intermolecular forces except during collisions.

How to find rms

Square all the values, divide it by the number of values, and then square root that number

Derivation of kinetic theory formula

velocity of particle before colliding with wall = c

velocity of particle after colliding with wall = -c

change in momentum = -2mc

t = 2l /c

force = (-2mc(x)²)/l

p(x) = F/A = F/l² = mc(x)² / l³ = mc(x)²/V - for one particle

for N number of particles = m(c(x)² ..... + c(Nx)²)/V

c(rms,x) = √(c(x)² ..... + c(Nx)²)/N

Nc²(rms,x) = (c(x)² ..... + c(Nx)²)

P(Nx) = (m/v) x N x c²(rms,x)

if motion is radom, magnitude of particles in x,y,z are reoughly the same

c² = c(x)² + c(y)² + c(z)²

c² = 3c(x)²

c²(rms) = 3c(rms,x)²

c²(rms)/3 = c(rms,x)²

P(Nx) = (m/v) x N x c²(rms) x (1/3)

Kinetic theory formula variables

p = pressure

v = volume

N = number of particles

m = mass of a particle

Nm/v = density

c²(rms) - to find speed, you square root it.

Fixed amount of gas, temperature is constant, volume decreases

discuss how the pressure changes

SA of gas reduces, so with the same force pressure will increase, P=F/A

The distance travelled between collisions is reduced , so there are more frequent collisions.

Temp is constant so velocity and force each particle exerts during each collision is constant.

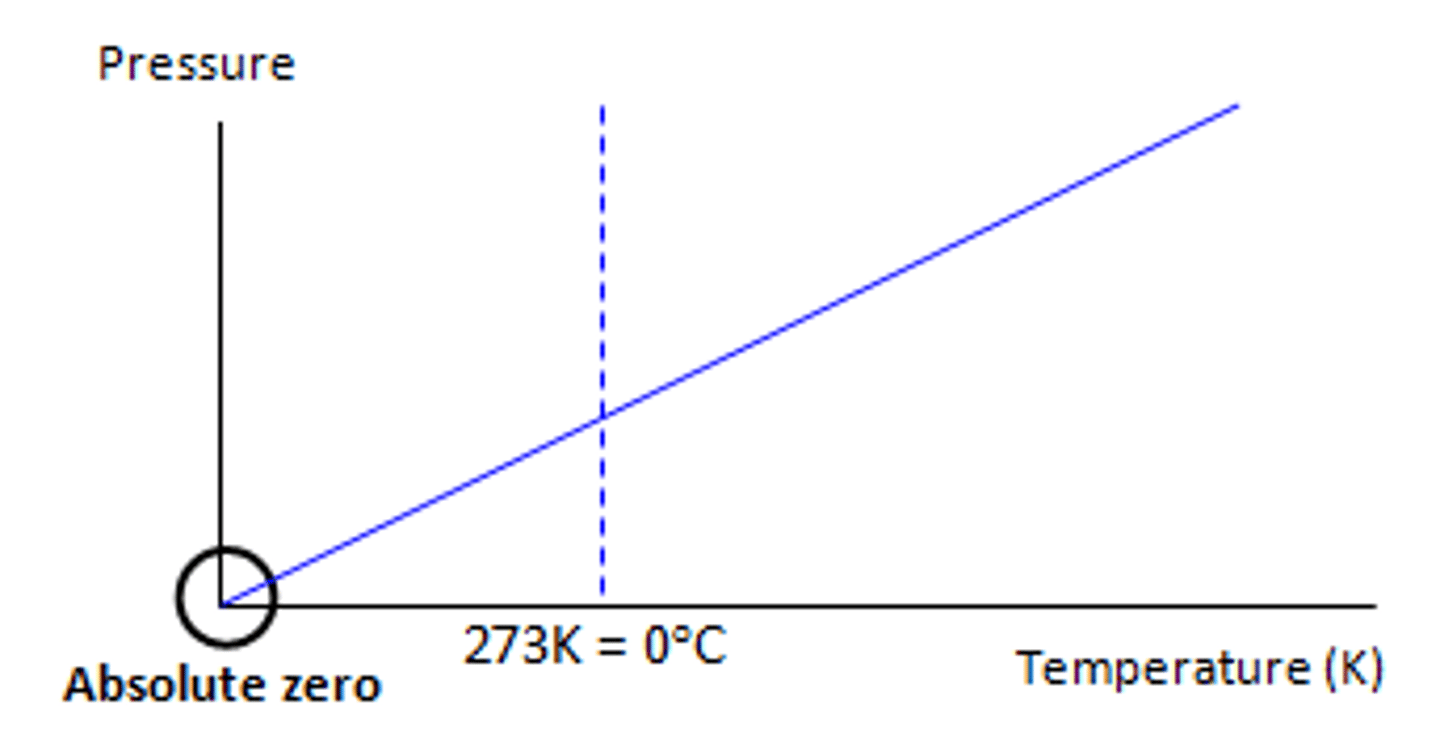
Absolute Temperature

Temperature is a measure of the average kinetic energy of the particles.

At absolute zero, particles would have no kinetic energy, and stop moving and therefore not exert a pressure.

Absolute temperature scale starts at zero.

Example would be Kelvin.

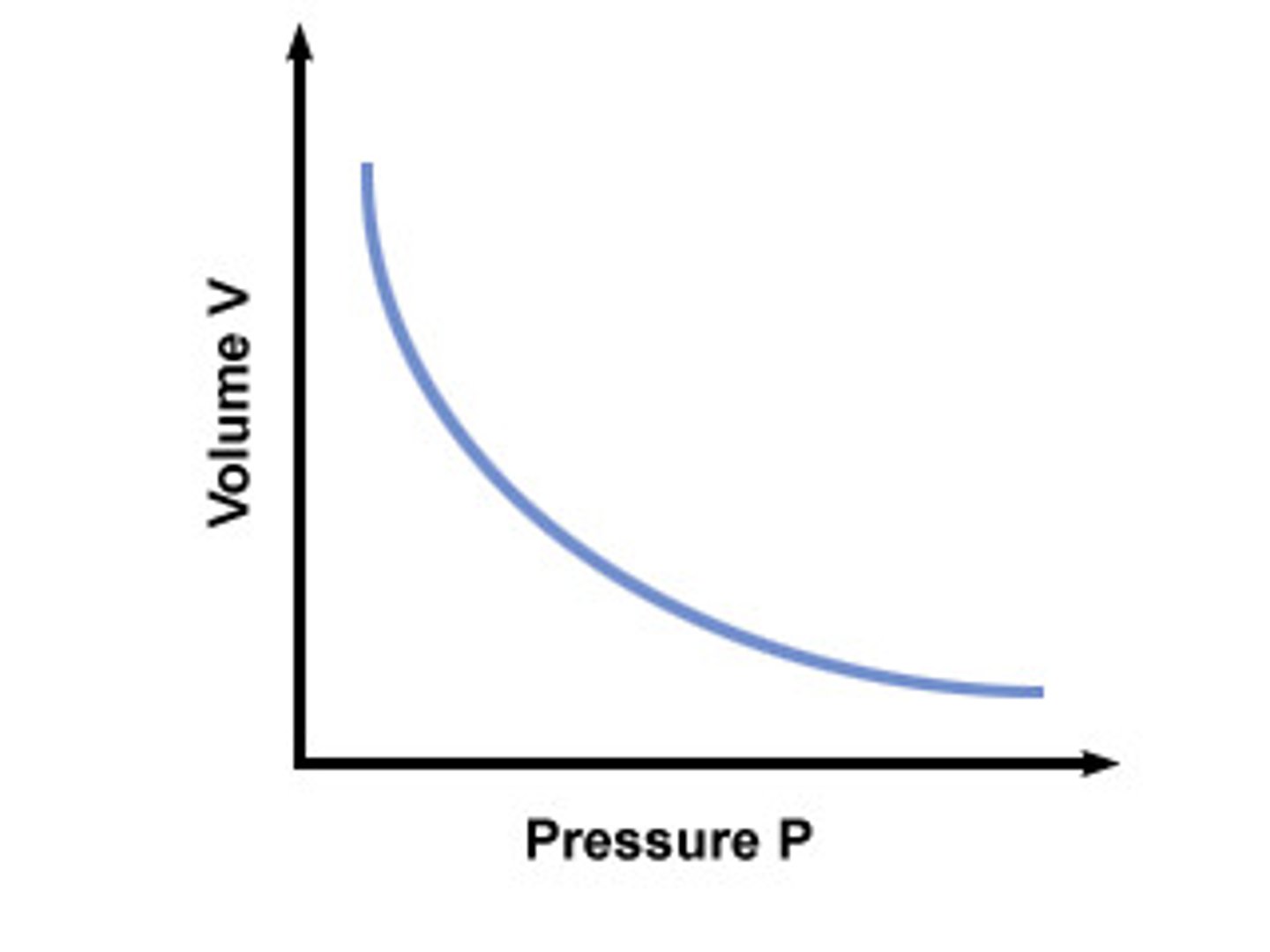
Boyles Law

For a fixed mass of gas at constant temperature, the pressure is inversely proportional to the volume.

Pressure Law

For a fixed mass of gas at constant volume the pressure is directly proportional to the absolute temperature.

Charles Law

For a fixed mass of gas at a constant pressure the volume is directly proportional to the absolute temperature.

Combining gas laws

PV/T = constant

P1V1/T1 = P2V2/T2

How to plot graph of variables that are inversely proportional?

One axis - 1/ first variable

Other axis - 2nd variable

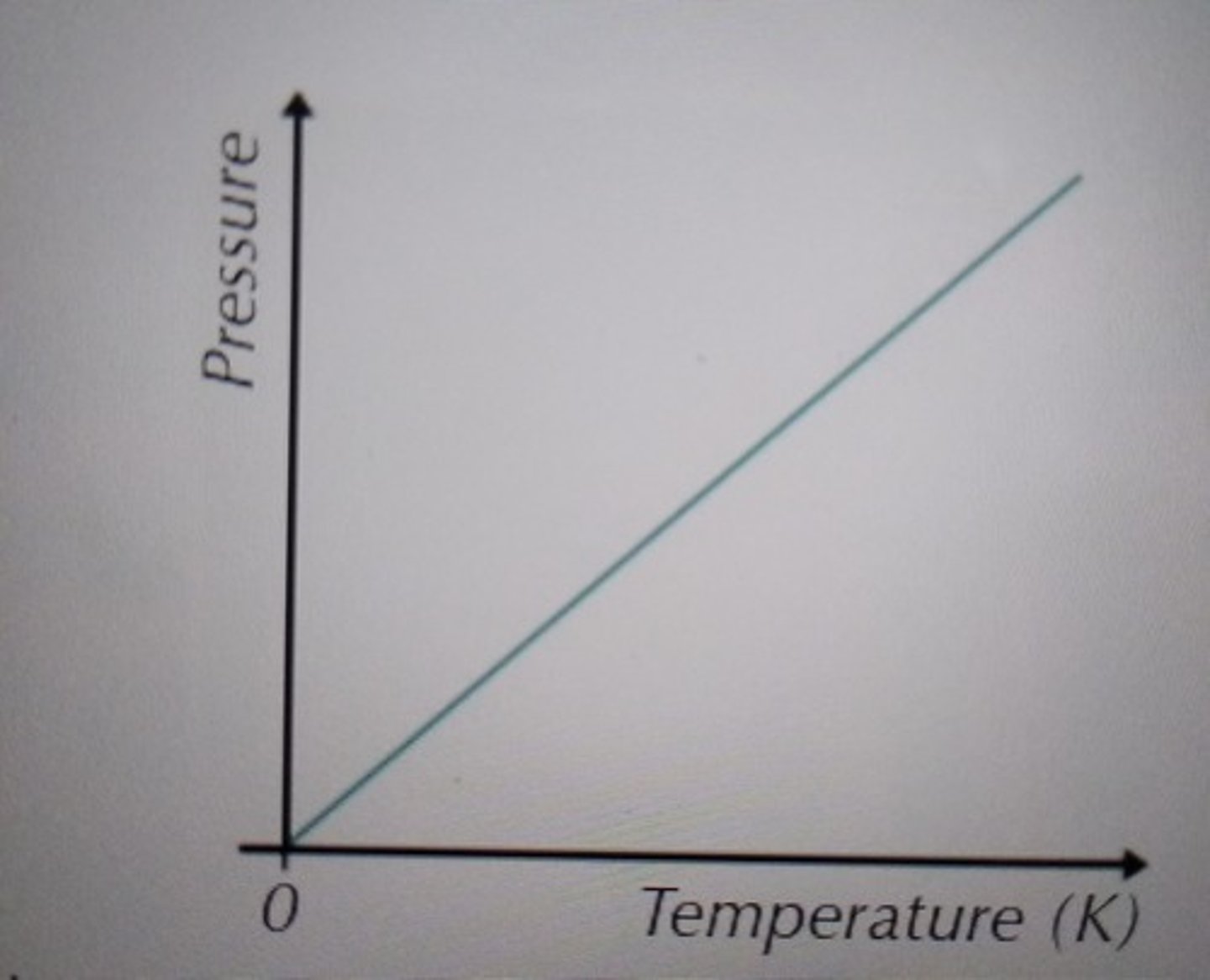
Pressure against absolute temperature (graph)

Pressure against temp in Celsius (graph)

Formulas for ideal gas laws

All equations in Kelvin.

PV = NkT , N = number of particles, k = 1.38 x 10^-23

PV = nRT, n = number of moles, R = 8.31

Equations to do with moles

N = number of particles, n= number of moles, NA = Avogadro's constant, m = mass , Mr = molar mass

N = n/NA

mass of substance = Mr x NA

mass of one particle = Mr / NA

How to find answer to do with change in mass or volume of a system?

have to use

PV = NkT or PV = nRT , use second one as easier numbers

cant use pv/t formula as density changes with change in mass or volume

find mass of new system

subtract mass of old system

thats increase in mass.

How to answer question with two flasks connected. finding mass or volume

Pressure of both is the same.

either equate the equations

or divide one by the other

how to find pressure after of connected vessel

for first flask find pressure after it occupies the entire volume of bath flasks.

then repeat for second flash.

add them together.

average molecular KE formula

1.5kT = 0.5 x m x c^2 rms

m - mass of one particle/molecule

when temp is doubled

you double the kelvin, not celsius

for complicated questions when stuck

find equation for both scenarios and then divide.

1 other formula

k = R x Na(Avogadro's constant)

increase temp...

ke and velocity of particles increase, force exerted increases

frequency of collisions increase due to increased speed,

root mean squared speed

mean squared speed

rms - √c^rms - m/s

ms - c^2rms -m^2/s^2

What's the difference between seatbelt and airbag?

same force

smaller area

higher pressure on parts of body

Total Kinetic energy

Average KE of one particles X number of particles

Ideal Gas

Molecules have negligible volume.

collisions are elastic.

Work done formula

W=PAd

W=P x change in Volume

PV graphs

Work done is area under the graph

Work is only done when volume changes

Work done on or by gas

On gas - compression and energy into gas.

By gas - Expansion and energy away from gas.

negative work done is work done by the gas.

Internal energy formula

ΔU = Q + W

Q - heat supplied to the gas. (Negative means heat is removed from the gas).

W is work done on the gas. (Negative means work done by the gas).

PV graph NTKs

Higher on graph = Higher Temperature

At fixed position and higher temp --- straight line up to T2.

Free to move and heated - Straight line across to T2.

For a fixed piston, that is heated will the gain of thermal energy be the same for a piston that is free to move?

ΔU = Q + W

For fixed piston : Is fixed so doesn't expand so no work is done. So ΔU = Q, which is heat supplied.

For a free piston: is free to move so will expand, when expands work is done by the gas, work done is negative.

ΔU = Q - W

So gain in thermal energy is larger for a fixed piston.

Draw on Graph

Temp from T2-T1 at constant pressure

Temp rise at constant volume

Straight Line across

Straight line up

Why does pressure decrease when there's less particles?

Pressure is due to collisions with walls.

Fewer particles, frequency of collisions with walls decreases.

But because temp is constant, velocity of particles and force exerted remains the same.

so total force exerted reduces.