Precalculus Review Quiz Review

What do you do when you don’t know how to factor something at all?

Check for a common factor to factor out

Sum of cubes factoring pattern

(x+y)(x²-xy+y²) → unfactorable trinomial

Difference of cubes factoring pattern

(x-y)(x²+xy+y²) → unfactorable trinomial

point slope format

y-y1=m(x-x1)

what is a normal line

perpendicular lines

logbase 4 of 8

you can just rewrite as an exponential equation, then rewrite using the same base, then solve

how to solve a problem with logs if the number wont go into that log

break into parts that can and cant. Then solve

what if you have 2 different exponents set equal to each other that use different bases?

use normal log on them and then take the exponents out as coefficients. Then simplify from there (at one point, x will have to be factored out of the equation)

If I have 47% decay over 7 years for a $61,000 car, how do I find the exponential function?

use total % depreciation to find percent reamining. Use this equal to the price times 1-x to the power of years.

how to find an exponential equation with the graphs

asymptote is k, then use points to find a and b (if need to find c, use the shift of point of (0,1) to find it

how do i switch ranges from [-1,4] to [0,4]?

First, set up system: -x+y=0; 4k+h=4. Solve system.

pi/6

sqrt(3)/2, 1/2

pi/4

sqrt(2)/2, sqrt(2)/2

pi/3

1/2, sqrt(3)/2

What to do when given a trig ratio and you need to solve for the others?

Use identities to find the ones you don’t know

range of arc functions

arcsin [-pi/2, pi/2]; arccos [0,pi]; arctan (-pi/2, pi/2), arccsc same without y=0, arcsec same without pi/2 or pi, arccot (0, pi)

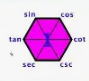
what does the trig magic hexagon look like? What can you find off of it?

quotient (go around, the next 2 are the N and D), product (the ones to the L and R are the factors), cofunction (sum of 2 angles to 90; go across horizontally), and pythagorean (use the triforce; go clockwise)

double angle identities for sin and tan

sin 2x=2sinxcosx, tan 2x = 2tanx/1-tan²x

double angle identities for cos

cos 2x =

• cos²x-sin²x

• 1-sin²

• 2cos²x-1

sum identities

• sin (x+y) = sinxcosy+cosxsiny

• cos (x+y) = cosxcosy-sinxsiny

• tan (x+y) = tanx+tan y/1-tanxtany

half angle

• sin x/2 = ± sqrt(1-cosx)/2

• cos x/2 = ± sqrt(1+cosx)/2

• tan x/2 = csc x + cot x