3.12.3 Special relativity

Michelson-Morley interferometer experiment

• Semi-silvered glass block (beam splitter) splits the beam of monochromatic light into two beams.

• The plane glass block (compensating plate) ensures that both beams pass through the same thickness of glass and air

• Beams travel at right angles, to mirrors , and return to/combine at telescope with a path difference

• Observer sees interference pattern from two beams

• Apparatus rotated 90 degrees and pattern observed

Expected result of Michelson-Morley interferometer

• Scientists used to believe in absolute motion, which is the idea that everything moves relative to the ether, which they believed was a substance which permeated the entire universe.

• Michelson and Morley believed that the speed of the light travelling parallel to the motion of the Earth would be affected, while the speed of light travelling perpendicular to the motion of the Earth would be left unaffected.

• So it was also believed the light moving parallel to the Earth’s motion will take longer to travel, therefore rotating the apparatus by 90° would cause a shift in the interference pattern as path length/speed of light is different depending on orientation relative to motion of apparatus so ether exists/absolute motion of Earth detected

Actual result of Michelson-Morley interferometer

No shift in pattern

Significance of actual result of Michelson-Morley interferometer

• No evidence of ether.

• The speed of light is invariant in free space, meaning that the speed of light is independent of the motion of the source or the observer.

Inertial frame of reference

• Inertial frames of reference are those which move at a constant velocity relative to each other, therefore a frame that is accelerating or rotating cannot be an inertial frame of reference.

• Einstein’s theory of special relativity only applies to inertial frames of reference.

2 postulates of Einstein’s theory of special relativity

• Physical laws have the same form in all inertial frames

• The speed of light in free space is invariant.

Time dilation

Time dilation is a consequence of special relativity, meaning it only occurs in inertial frames and causes time to run at different speeds depending on the motion of an observer.

Frame of reference of a stationary observer

The stationary observer’s frame of reference is stationary relative to the frame of reference where an event is occurring.

External observer

The frame of reference to an external observer is in motion.

Proper time t₀

• The amount of time passed experienced by the stationary observer (moving object).

• The proper time will always be shorter than the time measured by an external observer.

What does t represent in the special relativity equation for time dilation

Time measured by an external observer

State the measurements made and the observation that provides evidence for relativistic time dilation from muon decay.

• Number of muons passing through detector per second measured at top of mountain/in upper atmosphere.

• Number of muons passing through detector per second measured on ground.

• Measurements show far fewer muons decay than expected in time taken (in observer’s frame of reference) for muons to travel from upper atmosphere to ground as the clock in muons frame of reference runs slower than observer so half-life appears longer

Calculations made from muon decay which provides evidence for time dilation.

• Time taken for muons to move between detectors (t) can be calculated by distance/speed of light/muon.

• Divide this time by half life is the number of expected half lives in this time.

• The expected count rate will be initial count multiplied by 0.5^{(number of expected half lives)}.

• This is different from the observed count rate.

• The proper time can be calculated from the time dilation equation.

• Dividing this by the half life gives the calculated number of half lives in this time.

• The calculated count rate will be initial count multiplied by 0.5^{(calculated number of half lives)}.

• This gives a value close to the observed value providing evidence of time dilation.

Length contraction

Length contraction is a consequence of special relativity, meaning it only occurs in inertial frames and causes the length of objects moving at high speeds to appear shorter to an external observer

Proper length l₀

Length as measured by an observer who is at rest relative to the object.

Calculations made from muon decay which provides evidence for length contraction

• length (l) as it appears to the muons can be calculated from the length contraction equation.

• Dividing this length by the speed of muon/speed of light gives the time taken to travel this distance.

• Dividing this time by the half life of a muon gives the calculated number of half lives that occur in this time.

• The calculated count rate will be initial count multiplied by 0.5^{(calculated number of half lives)} this gives a value very close to the observed value.

Relationship between mass and energy

• In the theory of special relativity Einstein proved that mass and energy are interchangeable and can be related by the following equation:

• E=mc².

• Where E is energy, m is mass and c is the speed of light in a vacuum.

• Transferring energy to an object will cause its mass to increase, while transferring energy away from an object will cause its mass to decrease

• Because of this, the faster an object travels, the more massive it becomes.

Rest mass  m₀

• An object's proper mass (that is, its mass measured by an observer at rest relative to the object) is also called its rest mass, m₀

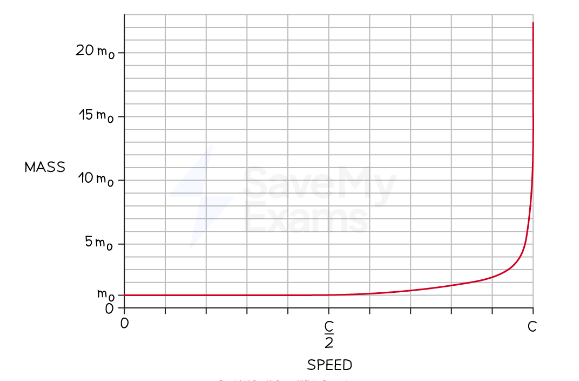
Relativistic mass

• An observer in an inertial reference frame moving at speed v  relative to the object measures the object's mass as m, which is given by m=m₀/√(1-(v²/c²)) or m=γm₀

How does relativistic mass vary with speed

• Because γ > 1, when an object is moving relative to your frame of reference, you measure its mass as larger than it's rest mass.

• As an object's speed nears the speed of light, it's mass gets larger and larger

• Very close to the speed of light, an object's mass tends towards an infinite mass.

Relitivistic energy

• E=mc².

• m=γm₀

• E=γm₀c²

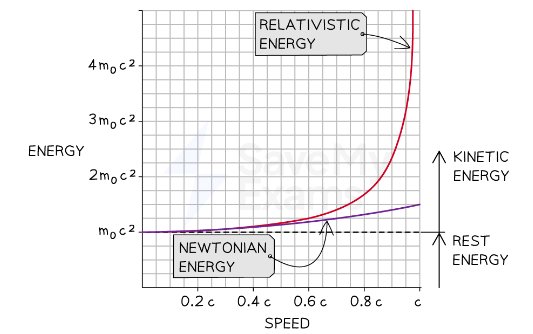
How does kinetic energy vary with speed

• E_k=0.5mv² does not apply for relativistic speeds over 0.1c because the mass of the object changes significantly

• We know that an object in motion relative to an observer has energy E = (γm₀)c² and its rest energy is E₀ = m₀c²

  • The kinetic store is the energy store associated with motion

  • If an object in motion has a total energy E which is greater than its rest mass E₀, the additional energy must be in the kinetic store

• E_k=mc²-m₀c²

• Where:

  • E_k is energy in the kinetic store

  • m is relativistic mass

  • m₀ is the object's rest mass

  • c is the speed of light

Bertozzis experiment

• Bertozzi’s experiment provides experimental evidence for the increase in mass of an object with speed.

• It involved:

  • A particle accelerator which could emit electrons at varying kinetic energies

  • Two detectors A and B connected to an oscilloscope

  • Aluminium plate connected to a temperature sensor:

• The electrons were released in pulses, and the time taken for them to travel between A and B could be calculated using the oscilloscope by measuring the distance between peaks on the display (and multiplying by the time base).

• Next, the distance between A and B is measured and the speed of the electrons was calculated.

• The electrons are directed at the aluminium target and when they collide with it, their kinetic energy is transferred to the target in the form of heat.

• The change in temperature of the target is measured using the temperature sensor, meaning the kinetic energy of the electrons could be directly measured.

• Kinetic energy of one electron=mcΔθ/n where m is the mass of the target, c is its specific heat capacity, Δθ is the change in temperature and n is the number of electrons in that pulse.

Significance of Bertozzis results

When Bertozzi plotted his results as a graph of kinetic energy against speed, he found that his values were very close to those predicted by Einstein’s theory of special relativity, meaning that his experiment provided evidence to support it.