Complex numbers (W3 mostly)

University of York, stage 1, semester 1, foundations and calculus. Complex numbers (week 3-5) basics.

how is a complex number (z) expressed in polar form?

z = a + bi = r(cosθ+ isinθ) = re^iθ

^{where r =|z|}

express a complex number in standard form.

What is the real and imaginary part?

z = a + bi

Re(z) = a, Im(z) = b

What is |z|?

Modulus of a complex number

sqrt(a² + b²)

What is z̄?

Complex conjugate of z. Where z = a +bi, z̄ = a  - bi

How do we divide complex numbers?

multiply by the complex conjugate of the denominator (like surds)

if z = a + bi and w = c = di then:

z/w = z/w * w̄

Proposition 2.8 (must prove all)

Properties of the complex conjugate and modulus

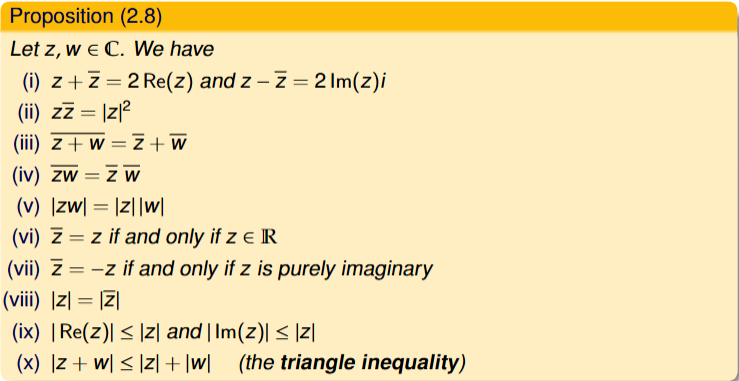
What are polar coordinates? 

(r,θ) where r is the distance from the origin to a point, and θ is the angle between x-axis and line from origin to a point. θ is anti-clockwise and in radians. 

What is the principal argument?

Let z = a + bi be a complex number

Principal argument θ of z is the unique value of θ ∈ ℝ such that

a = |z|cosθ, b = |z|sinθ and θ∈(−π,π]

Multiplication rule for complex numbers in polar form

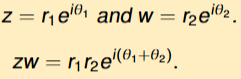
How to find the square root of a complex number? (standard)

w² = z so w = sqrt(z)

w = c + di

Solve (c + di)² = (a + bi) for c and d.

How to find the square root of a complex number? (polar) 

if z = re^iθ and w = se^iφ

Solve w² = z

s² e^i2φ = re^iθ has two solutions:

w₁= √r  e^i(θ/2) and w_z = √r * e^{i(θ/2 + π)} = -w₁

principal square root formula? Polar form

√r * e^i(θ/2)
Where θ is the principal argument of z.

What is the multiplicative inverse of a complex number?

Every complex number has a multiplicative inverse.

z^-1 := 1/z

z * z^-1 = 1

(to divide one number by another, you can multiply one number by the multiplicative inverse of another number)

What is De Moivre’s theorem? (2.15)

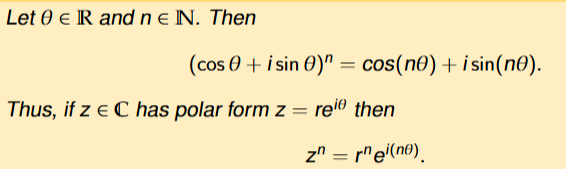
What is the binomial theorem?

What is the expression for the multiplicative inverse of a complex number in polar form?

z^-1 = 1/r * e^-iθ