W8L2: Dissociation of Water, Weak Acids and Bases, the Henderson–Hasselbalch Equation, and Buffers

Autoionization of Water

• A small fraction of water molecules dissociate spontaneously into hydrogen and hydroxide ions.

This reaction is reversible:

2 H2O ⇋. H3O+ + OH− or H2O ⇋. H+ + OH−

• At 25°C, only about 1 in 10⁷ molecules ionizes, but this equilibrium is essential for defining pH.

• Both ions are always present, even in pure water.

The Ion Product of Water

• Water is amphoteric—that is, water behaves as both an acid and a base. The full equation representing the dissociation of water can be written as follows.

• The equilibrium constant for water has a value of 1 × 10−14 at 25 °C. This means that only 1 in every 550 000 000 (1 in 5.5 × 108) molecules of water dissociates into ions.

• The equilibrium reaction lies almost totally to the left: the back reaction predominates hugely over the forward reaction. So we see that water is a very weak acid (and consequently a very strong base).

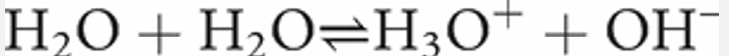
The concentration of acids: the pH scale

• pH Definition: pH measures the concentration of hydronium ions (H3O⁺) in a solution, indicating its acidity or basicity.

• Formula: pH= −log10[H3O⁺], where [H3O] is in mol L⁻¹.

• Scale Range: Typically 0–14 — low pH = acidic, high pH = basic, pH 7 = neutral.

• Purpose: Converts wide [H3O⁺] ranges (10⁻¹⁴ M to 10 M) into a simple, comparable numerical scale.

The Ion Product of Water (Kw)

Autoionization of Water: H₂O(l) ⇌ H⁺(aq) + OH⁻(aq)

Definition of Kw: Kw = [H⁺][OH⁻]

• At 25°C, Kw = 1.0 × 10⁻¹⁴

• In pure water, [H⁺] = [OH⁻]

• [H⁺] = [OH⁻] = Kw = 1.0 × 10⁻⁷ M

• pH = 7 → Water is neutral at 25°C

The concentration of acids: the pH scale

• Strong acids and bases dissociate completely in water, producing all available ions.

• An example of a strong acid is HCl

• Concentration of HCl in solution = Concentration of H+ ions

• Example of Strong base is NaOH

• Concentration of NaOH in solution = Concentration of OH- ions

Calculating pH of Strong Acids and Bases: Consider 0.1M HCl

HCl is a strong acid, meaning it dissociates completely in water: "HCl"→"H⁺"+"Cl⁻"

Thus, the concentration of hydrogen ions ["H⁺" ] is equal to the acid concentration.

["H⁺" ]=0.1" M"

Calculating pH of Strong Acids and Bases: Consider 0.1M NaOH

NaOH is a strong base, meaning it dissociates completely in water:

At 25 °C, the ion product of water is:

• 𝐾_𝑤=["H⁺" ]["OH⁻" ]=1.0×10^(−14)

Rearrange to find ["H⁺" ]:

• ["H⁺" ]=𝐾_𝑤/["OH⁻" ]

Calculate pH

"pH"=−𝑙𝑜𝑔10["H⁺" ]

"pH"=−𝑙𝑜𝑔10(1.0×10^(−13) )

log10(10^(−13) )=−13

"pH"=−(−13)=13

Importance of pH in Biological Systems

• Many enzymes are active only within narrow pH ranges.

• Even small pH changes can alter protein folding, function, and metabolic activity.

• Blood pH is tightly controlled between 7.35 and 7.45; deviation can be fatal.

• Biological fluids rely on buffer systems to maintain stability.

• Many biological molecules function as acids and bases because they can reversibly lose or gain protons (H+ ions) in a solution. This behavior is fundamental to life and is central to several key biological processes.

Weak acids and bases

• A weak acid or weak base only partially ionize in water.

• Weak Acid. 𝐻𝐴"  "⇌"  " 𝐻^++𝐴^−

• Weak Base. B + H2​O ⇌ BH+ + OH−

• The double arrow (⇌) indicates an equilibrium between undissociated acid (HA) and its ions.

Measure pH of weak acids and bases

• Acid Dissociation Constant (𝐾_𝑎)

• 𝐾_𝑎 ​ measures how much an acid dissociates into H⁺ and its conjugate base.

• mA large 𝐾_𝑎value means a stronger acid and greater proton donation.

• Small 𝐾_𝑎values indicate weak acids that ionize minimally.

• The 𝐾_𝑎 value is temperature-dependent and characteristic of each acid.

Acid Dissociation Constant Ka

The acid dissociation constant is exactly equivalent to the equilibrium constant. It merely tells us that we are specifically considering a reaction that represents the dissociation of an acid.

Relationship Between Ka and pKa

The strength of a weak acid can be expressed in two ways:

• Using the acid dissociation constant (Ka)

• Using its logarithmic form, pKa

Mathematical Relationship:

• pKa = −log₁₀(Ka)

• Ka = 10^(−pKa)

Interpretation:

• Small pKa → large Ka → strong acid

• Large pKa → small Ka → weak acid

Example:

For ethanoic acid, Ka = 1.8 × 10⁻⁵

pKa = −log(1.8 × 10⁻⁵) = 4.74

Thus, ethanoic acid has a pKa of 4.74, consistent with its weak acidity.

Linking weak acid strength and pH: using the Henderson–Hasselbalch equation

• A very important equation connects the Ka of a weak acid, the pH of a solution, and concentrations of the acid and its conjugate base.

• The relationship has widespread use in the biosciences, especially when it is necessary to control pH for optimum reaction conditions.

• The relationship is known as the Henderson–Hasselbalch equation, which we can write as:

• The variation in extent of dissociation of an acid with pH. Notice how the pKa is the pH at which the acid is 50% dissociated.

• When an amino acid such as aspartic acid (shown here) is exposed to a physiological pH of around 7.4—higher than its pKa value of 3.9—its side chain is highly dissociated such that the dissociation reaction lies heavily to the right. Consequently, at pH 7.4, this side chain carries a negative charge.

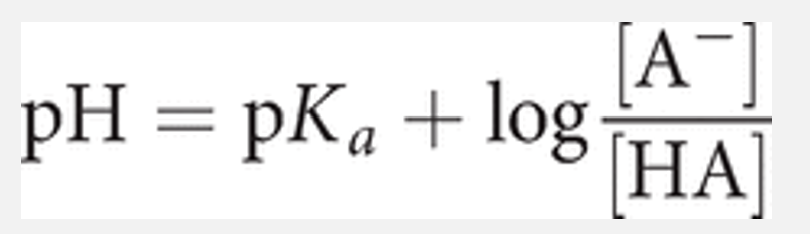
Biological Weak Acids and Bases

• Carbonic acid (H₂CO₃) plays a major role in blood buffering.

• Phosphoric acid (H₃PO₄) forms the phosphate buffer system inside cells.

• Amino acids contain both acidic (–COOH) and basic (–NH₂) groups.

• These weak acids/bases stabilize biological pH and mediate enzyme catalysis.

What is a Buffer Solution

A buffer is a solution that resists significant changes in pH when small amounts of acid or base are added.

It typically contains one of the following pairs:

• A weak acid and its conjugate base (e.g., CH₃COOH / CH₃COO Na)

• A weak base and its conjugate acid (e.g., NH₃ / NH₄ Cl)

Both components must be present in comparable concentrations.

The weak acid neutralizes added base (OH⁻), and the conjugate base neutralizes added acid (H⁺).

When acid (H⁺) is added: the conjugate base reacts with H⁺ to form the weak acid → minimal change in [H⁺].

A⁻ + H⁺ → HA

When base (OH⁻) is added: the weak acid donates a proton to neutralize OH⁻ → minimal change in pH.

HA + OH⁻ → A⁻ + H₂O

Pure water cannot resist pH changes — even small additions of strong acid or base cause large shifts in [H⁺].

Buffers prevent such drastic pH swings, which is essential for biological systems (e.g., blood pH ≈ 7.4).