LESSON 4: Scores and Standard Normal Distribution

Normal Distribution

also known as the “bell curve”, is the most important and most widely used distribution in statistics

Normal Distribution

It is also called the “Gaussian curve” of Gaussian distribution after the mathematician Karl Friedrich Gauss

Standard Normal Distribution

A _ has a mean of zero and a standard deviation of 1

Features of Normal Distributions

1. Normal Distributions are symmetric around their mean. 

2. The mean, median, and mode of a normal distribution are equal.

3. The area under the normal curve is equal to 1.0.

4. Normal Distributions are denser in the center and less dense in the tails.

5. Normal distributions are defined by two parameters, the mean ( μ) and the standard deviation (σ)

6. 68% of the area of a normal distribution is within one standard deviation of the mean.

7. Approximately 95% of the area of a normal distribution is within two standard deviations of the mean.

True

True or False

Normal Distributions are symmetric around their mean. 

True

True or False

The mean, median, and mode of a normal distribution are equal.

True

True or False

The area under the normal curve is equal to 1.0.

True

True or False

Normal Distributions are denser in the center and less dense in the tails.

True

True or False

Normal distributions are defined by two parameters, the mean ( μ) and the standard deviation (σ)

True

True or False

68% of the area of a normal distribution is within one standard deviation of the mean.

True

True or False

Approximately 95% of the area of a normal distribution is within two standard deviations of the mean.

Kurtosis

refers to the degree to which the distribution of data is flat or peaked

Mesokurtic

 considered to be closest to normal

Leptokurtic

peaked distribution

Platykurtic

flat

z-SCORE

a standardized version of a raw score (x) that gives information about the relative location of that score within its distribution

True

True or False

Raw score means nothing and z-scores are golden

For Population (z-Score)

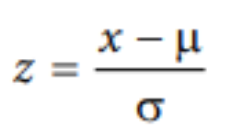
For Sample (z-Score)

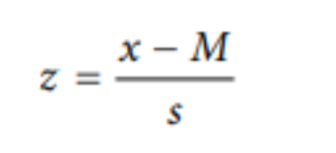
Scale

how far apart the scores are (their spread) and where they are located (their central tendency)

Standard Score

raw score that has been converted from one scale to another scale

For Population (Setting The Scale of a Distribution)

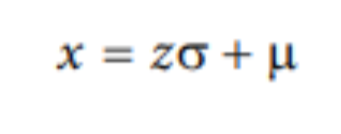
For Sample (Setting The Scale of a Distribution)

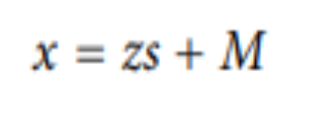
Normalized Standard Score Scale: Z-Score

Mean: 0

SD: 1

Normalized Standard Score Scale: T-Score

Mean: 50

SD: 10

Normalized Standard Score Scale: Stanine

Mean: 5

SD: 2

Normalized Standard Score Scale: STEN

Mean: 5.5

SD: 2

Normalized Standard Score Scale: IQ

Mean: 100

SD: 15

Standardization

a process of converting all of the scores in the distributions into z scores; a process where different variables are put on the same scale

Area Under the Curve

bounded by a single z score or pair of z scores

• always equal to 1.0

Area in the Tails of the Distribution

 the proportion of the area outside the deviation

True

True or False

All normal distributions are symmetrical.

2.

False

True or False

All normal distributions have a mean of 1.0

False

True or False

All normal distributions have a standard deviation of 1.0.

True

True or False

The total area under the curve of all normal distributions is equal to 1

What does a z score of 0.00 represent?

indicates that the data point is identical to the mean of the standard normal distribution.