Materials Exam 2

If the true stress of a prismatic member under uni-axial tension is defined as the force divided by the instantaneous cross-sectional area of the member, then the true stress should always be

 

Larger than the engineering stress

The Young’s modulus of a material at a certain temperature

 

is a constant and cannot be changed by, e.g., deformation

The stress-strain curve of any elastic material must be a straight line

False

Hooke’s law applies to any elastic material

False

If a prismatic member is under uni-axial loading in the x-axis, then in the y- and z-directions, there will be no strains

False

The tensile strength of a material is

 

the maximum stress in the engineering stress-strain curve.

When the strain is small, the differences between the engineering quantities (strain and stress) and the true quantities are very small, too.

True

When deriving the relations between the true and engineering stresses and strains, we use the following basic assumption:

 

The volume of the material does not change.

By definition, resilience is the capacity of a material to absorb energy when it is deformed elastically and then, upon unloading, to have this energy recovered. Therefore, the modulus of resilience, U_r, is a constant like the Young’s modulus, and cannot be changed by heat-treatment or plastic deformation.

False

Hardness is defined as

 

the resistance of a material to local plastic deformation.

If the Vickers hardness number of a metal is measured to be 600 (kg/mm² ), then its yield strength is roughly

 

200 (kg/mm^2).

For a given specimen under uni-axial compression, the true stress-strain curve is

 

below the engineering stress-strain curve.

The following statement is always correct: The stronger a material, the more energy is needed to fracture it.

False

To find the parameters in the Hollomon equation (), we use stress-strain data from the plastic regime before necking of the

 

true stress-strain curve.

If we load an annealed metal such as copper beyond its yield strength into the plastic regime, and unload to zero stress. During reloading of the metal, its yield strength will be

 

greater than the previous yield strength.

The ability of a metal to plastically deform depends on:

 

How easy dislocations can move within the crystal lattice.

The yield strengths of metals are much smaller than the theoretical strength because:

 

There are always dislocations within the metals which are responsible for plastic deformation, and whose motion only requires stress levels much smaller than the theoretical strength of the metals.

All metals, regardless of their crystal structure, have the same ability of plastic deformation at the same temperature.

Fasle

A single crystal metal will yield at the same stress level regardless of the orientation in which it is loaded. In other words, the yield strength of a single crystal metal is a constant and will not depend on the direction in which the stress is applied.

False

A polycrystalline metal with finer grain size is stronger (that is, it has higher yield strength) than a coarser-grain counterpart because:

 

It has more grain boundaries which are barriers to dislocation motion.

All strengthening mechanisms are at the cost of fracture toughness.

False

Among the typical strengthening mechanisms, the following will increase the yield strength and toughness concomitantly:

 

Grain size refinement hardening (or Hall-Petch hardening).

For a polycrystalline metal to have uniform plastic deformation under stress, the metal should have at least the following number of independent slip systems:

Five

When a plastically deformed metal is annealed at elevated temperatures, the three stages that occur, in the appropriate order, are

 

Recovery, recrystallization and grain growth.

During recovery of a plastically deformed metal, the following processes occur:

 

Dislocations are coming together, annihilated, and re-arranged into low energy dislocation configurations.

Ductile failure means there is a large plastic deformation before failure. Brittle failure means there is little plastic deformation before failure.

True

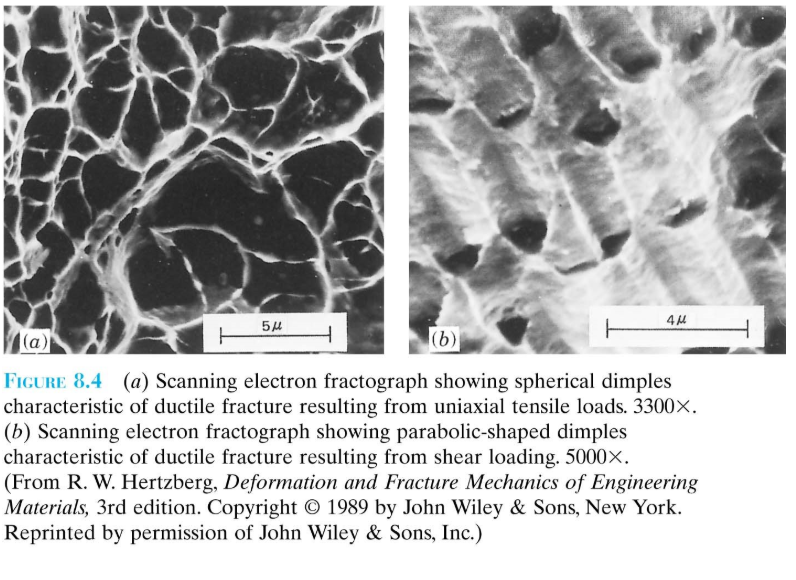
See the following fracture surface images of two materials.

 

Image (a) represents ductile fracture and image (b) represents brittle fracture.

The higher the ductile-to-brittle transition temperature of a metal, the better its fracture toughness.

False

The most important assumptions of Griffith theory for brittle fracture include:

 

The material is linear elastic (Hooke’s law holds) and has no plastic deformation.

For a completely brittle material, a crack of any size will grow under any applied stress.

False

The stress intensity factor, K, is calculated as: K=Y.σ.√(π.a), where Y is a geometry factor with no unit assigned to it, σ. is the stress (MPa), and a is the surface crack length (m). The unit of K is then:

 

MPa.m^(1/2)

The plane strain fracture toughness of a steel K_IC, is a material property and therefore cannot be changed by heat-treatment.

False

All materials will have a fatigue limit which is the largest value of fluctuating stress that will not cause fatigue failure for essentially an infinite number of cycles.

False

Fatigue can occur only when the maximum stress is tensile and the minimum is compressive.

False

Creep of a material can occur at any temperature.

False