Lecture 10: Beam Deflection

Flashcards covering key terms and definitions related to beam deflection in structural engineering.

Deflection

A stiffness requirement and is a change in position of a beam due to applied loads.

Important factors in determining deflection are:
Load
Modulus of Elasticity (E)
Length
Moment of Inertia (I)
Excessive deflections are undesirable in a building structure for a variety of reasons.

Modulus of Elasticity (E)

A measure of a material's ability to deform elastically when a load is applied.

Moment of Inertia (I)

A property of a beam that affects its resistance to bending.

Deflection limits

The maximum allowable deflection of beams as specified by building codes.

Principle of Superposition

A method used to calculate the effect of multiple loads on a beam by assessing each load individually and summing their effects.

Live Load (LL)

The load that is not permanently applied to a structure, such as people or furniture.

Dead Load (DL)

The permanent static weight of the structure itself.

Deflection table

A reference table that provides formulas for calculating deflection under various loading scenarios.

For example, large beam deflections in roof beams can result…

cracking of the attached ceiling and walls.

Large deflections in lintels can also cause…

improper functioning of doors and windows. Therefore, calculation and control of the beam deflection is calculated based on a series of tabulated formulas.

Once the beam deflection is calculated for a specified load, it must be…

compared against a value which is suggested by codes. The deflection limits, provided by various building codes, vary based on the load type and the location of the beam within the structure.

Deflection Limits: ROOF BEAMS Total Load (DL+LL)

L/180

Deflection Limits: ROOF BEAMS Live Load (LL)

L/240

Deflection Limits: FLOOR BEAMS Total Load (DL+LL)

L/240

Deflection Limits: FLOOR BEAMS Live Load (LL)

L/360

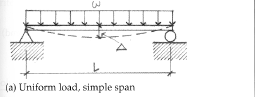
Beam deflection Formula: Uniform load (UDL), simple span

Δ_max = 5wL⁴ /348EI (at the centerline)

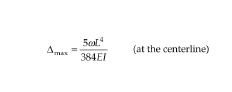
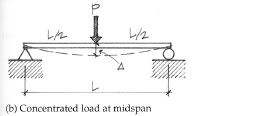
Beam deflection Formula: Concentrated (point) load at midspan

Δ_max = PL³ /48EI (at the centerline)

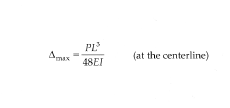
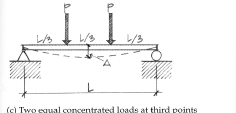
Beam deflection Formula: Two equal concentrated (point) loads at third points

Δ_max = 23PL³ / 648EI = PL³ / 28.2EI (at the centerline)

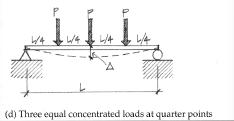
Beam deflection Formula: Three equal concentrated (point) loads at quarter points

Δ_max = PL³ /20.1EI (at the centerline)

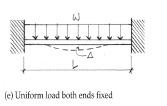
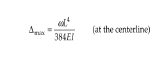
Beam deflection Formula: Uniform load (UDL) both ends fixed

Δ_max = wL⁴ /384EI (at the centerline)

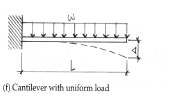
Beam deflection Formula: Cantilever with uniform load (UDL)

Δ_max = wL⁴ /8EI (at the free end)

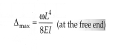
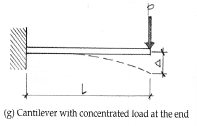
Beam deflection Formula: Cantilever with concentrated (point) load at the end

Δ_max = PL³ /3EI (at the free end)

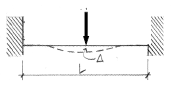
Beam deflection Formula: Beam fixed on both sides, point load in the middle

Δ_max = PL³/192EI (at the centerline)

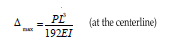
The principle of superposition is used to calculate the beam deflection for…

combined loading conditions.

The concept of superposition consists of…

finding the effect of several loading conditions that are acting on a beam simultaneously by determining the effect of each individual load on the beam separately.

The deflection values for the individual loads can be obtained from the deflection tables and then added to get the total deflection for the beam. (solve individually then combine to get total deflection)