HYPOTHESIS TESTING - POWER

por Hernandez Diaz Rosalba Arizbeth

Poder: 1−β

: La probabilidad de rechazar la hipótesis nula (H0) cuando es falsa.

¿Qué es la probabilidad de cometer un error Tipo II (β)?

La probabilidad de aceptar la hipótesis nula (H0) cuando es falsa.

Relación entre el poder del test y el error Tipo II.

1−β es el poder de la prueba. Si β es la probabilidad de cometer un error Tipo II, entonces 1−β es la probabilidad de evitar un error Tipo II.

Si la media de la población de la hipótesis nula (μ 0) es 180 mg/100 ml y la verdadera media de la población (μ

1 ) es 211 mg/100 ml. ¿Cuál sería la probabilidad de rechazar la hipótesis nula si la significancia (α) se establece en 0.05 y el poder (1−β) es 0.958?

La probabilidad de cometer un error Tipo II (β) sería 1−0.958=0.042. (Esto se refiere al gráfico "Curva de poder para μ0=180,α=0.05, y n=25").

La relación entre α (significancia) y β (error Tipo II).

Un compromiso entre α y β se observa en el análisis de las curvas de distribución. Aumentar el tamaño de la muestra puede ayudar a reducir el solapamiento entre las distribuciones y, por lo tanto, disminuir α y β simultáneamente.

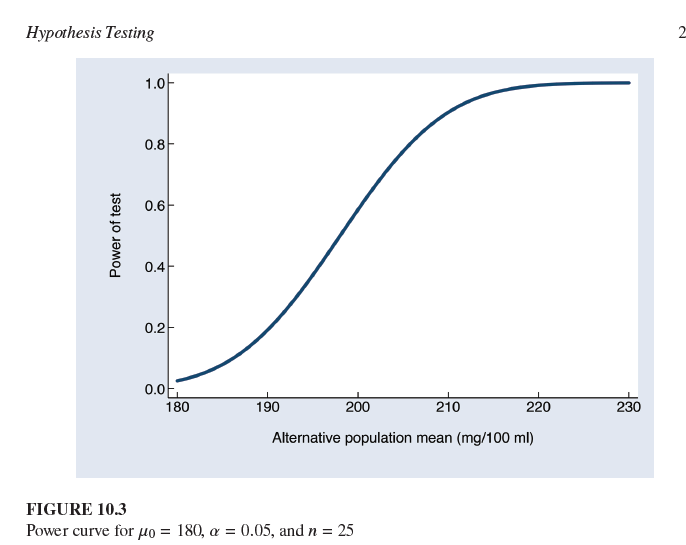
¿Qué muestra este gráfico?

La curva de poder, que ilustra cómo el poder de la prueba cambia con diferentes valores de la media de la población alternativa (μ1).

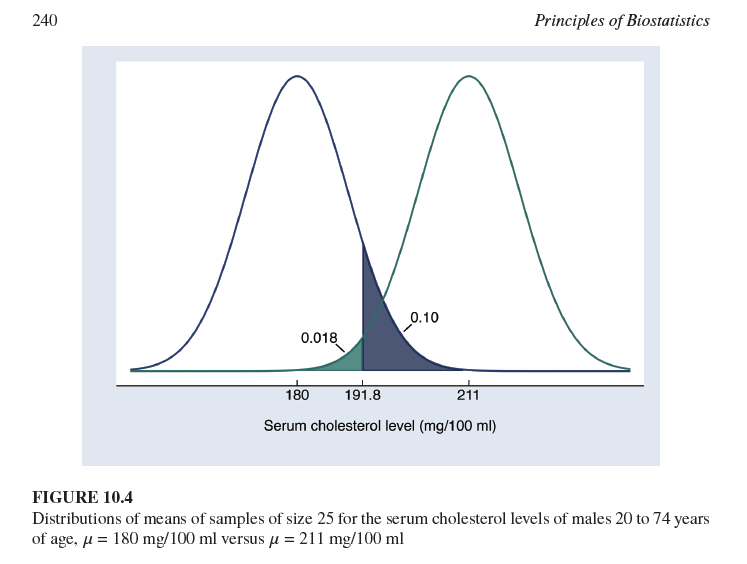
¿Qué representan las áreas sombreadas en este gráfico?

El área sombreada a la derecha de la curva de μ0 (0.018) representa la probabilidad de un error Tipo I (α) si el punto de corte para el rechazo es 191.8 mg/100 ml.

El área sombreada a la izquierda de la curva de μ1 (0.10) representa la probabilidad de un error Tipo II (β) si el punto de corte para el rechazo es 191.8 mg/100 ml.

Sensibilidad y especificidad en pruebas diagnósticas.

La sensibilidad y la especificidad de una prueba son análogas al poder de la prueba y al error Tipo I, respectivamente. Mejorar la sensibilidad puede reducir el error Tipo II, mientras que mejorar la especificidad puede reducir el error Tipo I.

¿Cómo se puede reducir el solapamiento entre las distribuciones en el contexto de las hipótesis nula y alternativa?

Aumentando el tamaño de la muestra (n). Esto reduce el error estándar de la media (σ/n).

P (rechazar H0 ∣H0 es falsa)

Esta es la definición de poder (1−β).

Una prueba realizada con un nivel de significancia de 0.05 (α=0.05) y un tamaño de muestra de 25 (n=25). La verdadera media poblacional (μ1) es 211 mg/100 ml, y la hipótesis nula (H0) establece que μ≤180 mg/100 ml.

Si el poder (1−β) es 0.958, ¿cuál es la probabilidad de aceptar la hipótesis nula cuando es falsa?

1−poder=1−0.958=0.042. Esta es la probabilidad de un error Tipo II (β).

La relación entre α y β cuando el tamaño de la muestra es fijo.

Típicamente, aumentar α (la probabilidad de un error Tipo I) disminuirá β (la probabilidad de un error Tipo II), y viceversa. Hay una compensación.

¿Qué ilustra una "curva de poder"?

Una curva de poder ilustra cómo el poder de una prueba cambia para diferentes valores de la media de la población alternativa (μ1 ) (u otros parámetros bajo la hipótesis alternativa), dado un tamaño de muestra y un nivel de significancia fijos.

Impacto del tamaño de la muestra en las pruebas de hipótesis.

Aumentar el tamaño de la muestra (n) generalmente aumenta el poder de una prueba porque reduce el error estándar de la media (σ/n ), haciendo que las distribuciones de las hipótesis nula y alternativa se superpongan menos.

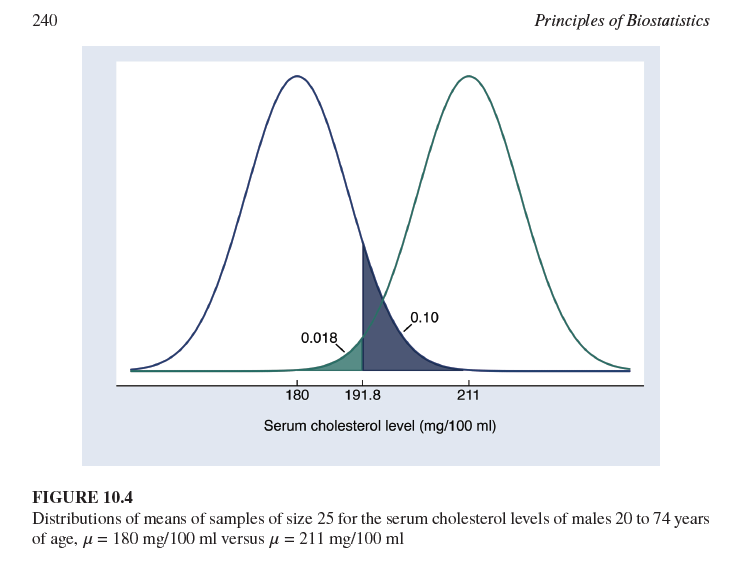
¿Cuál es la probabilidad de un error Tipo I (α) si el punto de corte para el rechazo es 191.8 mg/100 ml y la media de la hipótesis nula es 180 mg/100 ml?

0.018 (como se muestra en el gráfico, el área a la derecha de 191.8 bajo la curva de 180 mg/100 ml).

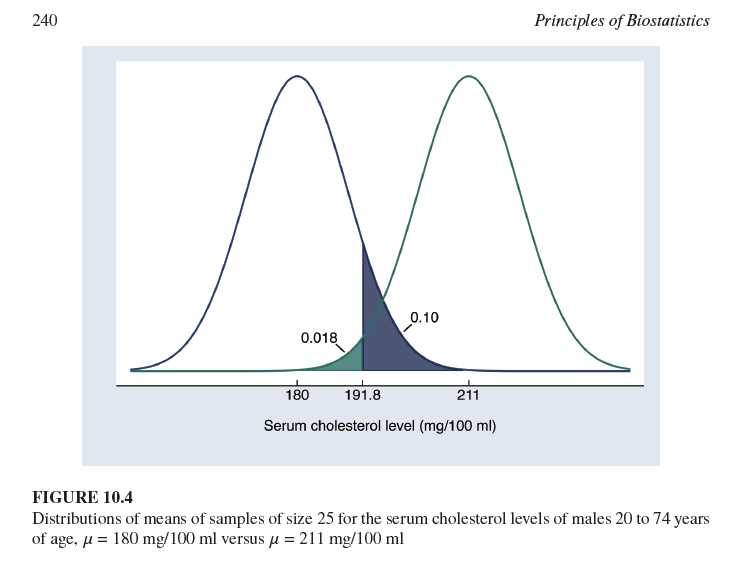
¿Cuál es la probabilidad de un error Tipo II (β) si el punto de corte para el rechazo es 191.8 mg/100 ml y la verdadera media poblacional es 211 mg/100 ml?

0.10 (como se muestra en el gráfico, el área a la izquierda de 191.8 bajo la curva de 211 mg/100 ml).

Interpretación de una desviación de la hipótesis nula en los cálculos de poder.

Se asume que una desviación de la hipótesis nula, representada por μ1, es lo suficientemente grande como para que un estudio en particular la detecte. μ1  debe calcularse para una media de población alternativa específica.

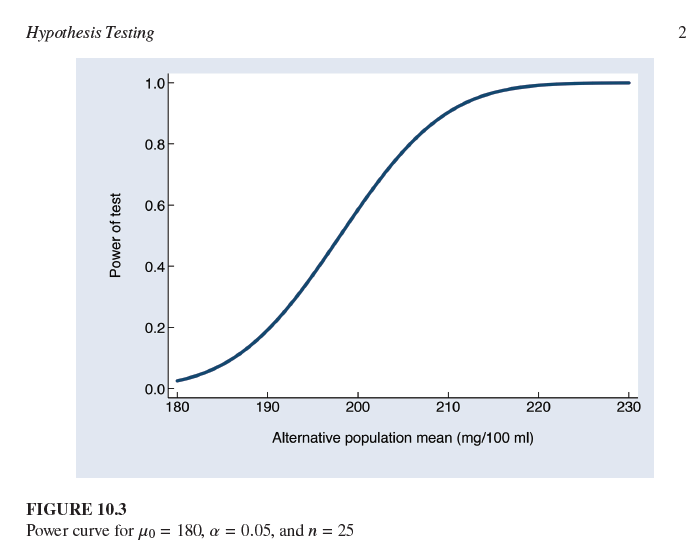
¿Qué significa un 95.8% de probabilidad de rechazar la hipótesis nula en el contexto de la "Curva de poder para μ0=180,α=0.05, y n=25" (Figura 10.3)?

Representa el poder (1−β) de la prueba cuando la verdadera media poblacional (μ1) es 211 mg/100 ml.

El objetivo de la Prueba de Hipótesis

Determinar si hay suficiente evidencia para rechazar una hipótesis nula, a menudo comparando una estadística muestral observada con un parámetro poblacional hipotetizado.

¿Cuál es la utilidad de calcular varios valores de 1−β frente a todas las posibles medias de población alternativa?

Permite trazar una curva de poder, que proporciona una representación visual de cómo el poder de la prueba cambia a través de un rango de hipótesis alternativas.

¿por qué es importante mejorar la sensibilidad de una prueba diagnóstica?

Mejorar la sensibilidad de una prueba diagnóstica disminuye la probabilidad de un error Tipo II (β), lo que significa que reduce la probabilidad de falsos negativos.

¿por qué es importante mejorar la especificidad de una prueba diagnóstica?

Mejorar la especificidad de una prueba diagnóstica disminuye la probabilidad de un error Tipo I (α), lo que significa que reduce la probabilidad de falsos positivos.

La relación entre el error Tipo I (α) y el error Tipo II (β) en términos prácticos.

Reducir un tipo de error a menudo lleva a un aumento en el otro, asumiendo que todos los demás factores (como el tamaño de la muestra) permanecen constantes. Esto destaca la "compensación" que los investigadores deben considerar.

El texto compara "personas culpables" con "persona inocente".

En el contexto de una prueba de hipótesis estadística, ¿Qué podría representar una "persona culpable"?

Un caso en el que la hipótesis nula es falsa (es decir, hay un verdadero efecto o diferencia).

El texto compara "personas culpables" con "persona inocente".

En el contexto de una prueba de hipótesis estadística, ¿Qué podría representar una "persona inocente"?

Un caso en el que la hipótesis nula es verdadera (es decir, no hay un verdadero efecto o diferencia).

Interpretación de P(Z≥1.73) en el cálculo de poder. En el cálculo "poder = P(Z >= 1.73)", ¿qué representa probablemente el valor "1.73"?

Representa el valor crítico z (o la estadística de prueba estandarizada) correspondiente a la región de rechazo bajo la hipótesis nula, ajustado para la hipótesis alternativa.

¿Cuál es la regla general mencionada con respecto a la desviación estándar de la población subyacente en el contexto de las pruebas de hipótesis?

Generalmente se asume que la desviación estándar de la población subyacente (σ) es conocida, o que puede estimarse razonablemente a partir de estudios previos.

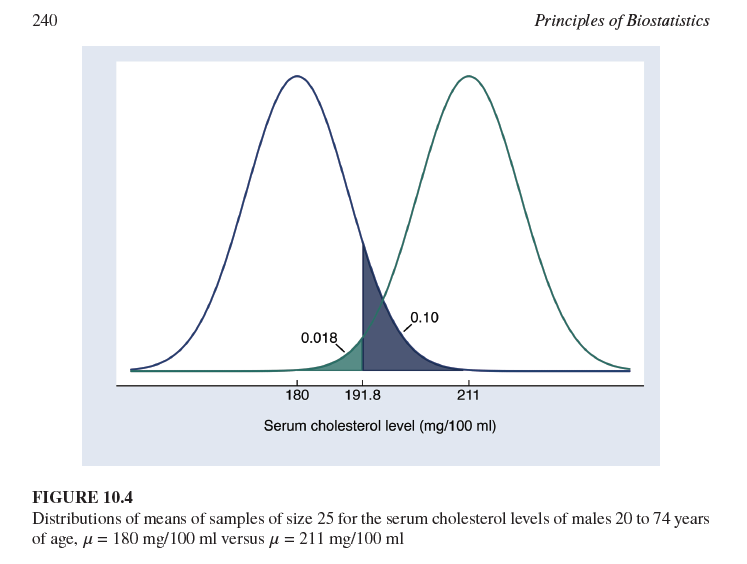
La Figura 10.4 muestra dos distribuciones normales centradas en μ0=180 mg/100 ml y μ1=211 mg/100 ml. ¿Qué representa la desviación estándar de estas distribuciones muestrales?

Representa el error estándar de la media, calculado como σ/n, donde σ es la desviación estándar de la población y n es el tamaño de la muestra (25 en este caso).

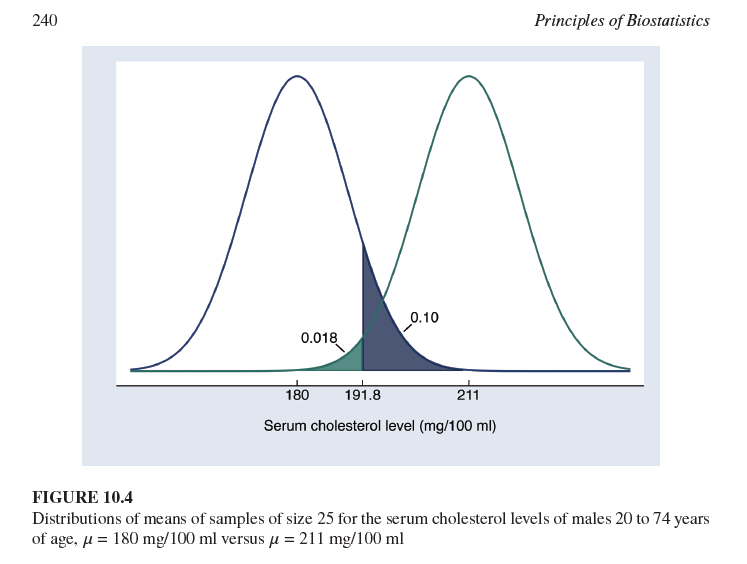
¿Cuál es la diferencia fundamental entre la distribución centrada en μ0 y la centrada en μ1 en la Figura 10.4?

La distribución centrada en μ0 representa la distribución muestral de la media si la hipótesis nula fuera verdadera, mientras que la distribución centrada en μ1 representa la distribución muestral de la media si la hipótesis alternativa fuera verdadera (específicamente, si la media verdadera fuera 211 mg/100 ml).

¿Cómo mejora el aumento del tamaño de la muestra la capacidad de distinguir entre las hipótesis nula y alternativa?

Aumentar el tamaño de la muestra reduce el error estándar de la media, haciendo que las distribuciones muestrales sean más estrechas y disminuyendo su solapamiento. Esto permite una mejor discriminación entre las dos hipótesis, aumentando así el poder (1−β) para un α dado.