CSC645 - Chapter 6 - Dynamic Programming ADT

Dynamic Programming (DP) ADT Overview

1. History / Definition

   • Invented by Mathematican , Richard E Ballman

   • The term “programming” actually refers to planning

2. DP attempts to solve problems with overlapping subproblems (Rather than solve the same problem again & again, we store them in a table)

Dynamic Programming (DP) ADT DP Properties

1. Overlapping sub-problems

   • → same sub-problem occur more than once

2. Optimal substructure

   • → final solution = combination of optimal solution (from small solution, merge and get the final solution)

Overlapping sub-problems?

• Solve 2 times or more DP attempts to solve problems with overlapping sub-problems

• Eg: Fib (5)

Original solution:

 fun Fib(n)
 	if n=0|| n=1
 		return 1,
 	else return Fib(n-2) + Fib(n-1) 

• Just read from the table: • E.g. Fib(8)

DP: Transitive Closure (Warshal) War (2 pihak)

1. Transitive closure means connectivity

2. Is there a path for every node to all other nodes?

   • E.g. 1:

     • A can go to all node?

     • B can go to all node?

     • C can go to all node?

3. DP algorithm that can solve this problem is *Warshal

• E.g. 1

• E.g. 2

• E.g. 3

DP: All-Pair Shortest Path (Floyd Warshal)

1. Finding the shortest path from any nodes to all other nodes.

2. DP algorithm that can solve this problem is Floyd Warshall (Have weightage)

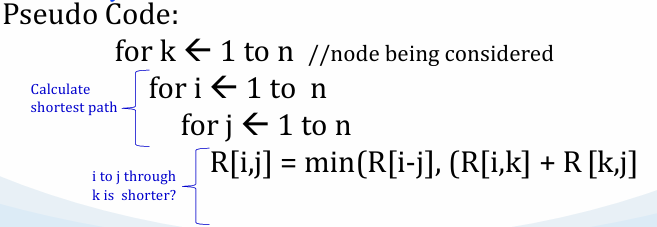
• E.g. 1:

DP: Knapsack

1. Choosing subset of n items that will fit a given constraints and yield maximum value.

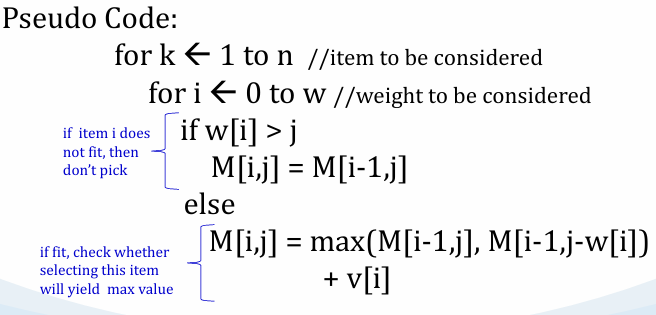
• E.g.1

• E.g.2