Grade 11 Geometry: Triangles, Circle Geometry, and Quadrilaterals (Video Notes)

Vocabulary flashcards covering triangles, circle geometry, and quadrilaterals from the video notes.

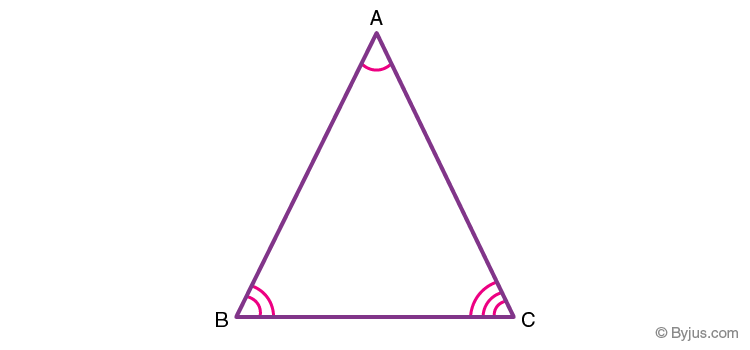
Interior angles of a triangle

The sum of the three interior angles in any triangle is 180 degrees.

Exterior angle of a triangle

An exterior angle equals the sum of the two interior opposite angles.

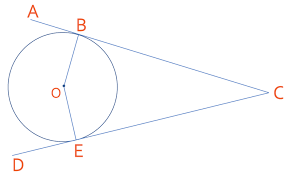
AC and DC are tangents

BC = EC

Reason: tangents from same point

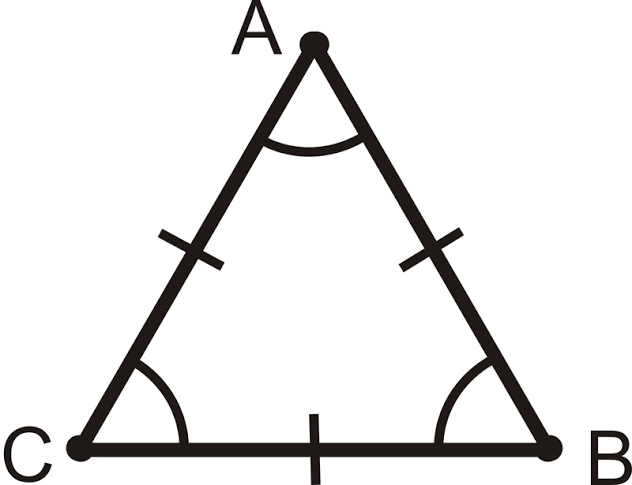
Equilateral triangle

A triangle with all sides equal and all interior angles equal to 60°.

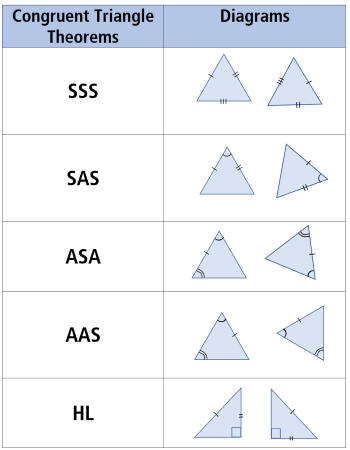
Congruent triangles definition and proofs

Two triangles that are exactly the same in size and shape; all corresponding angles and sides are equal.

Congruency vs similarity symbol

Congruency ≅

Similarity III

SSS (Side-Side-Side) criterion

If all three corresponding sides of two triangles are equal, the triangles are congruent.

SAS (Side-Angle-Side) criterion

If two sides and the included angle of two triangles are equal, the triangles are congruent.

AAS/SAA/ASA criteria

If two angles and a non-included side (or two angles and the included side) are equal, the triangles are congruent.

RHS (Right-Angle–Hypotenuse–Side) criterion

In right triangles, if the hypotenuse and one other side are equal, the triangles are congruent.

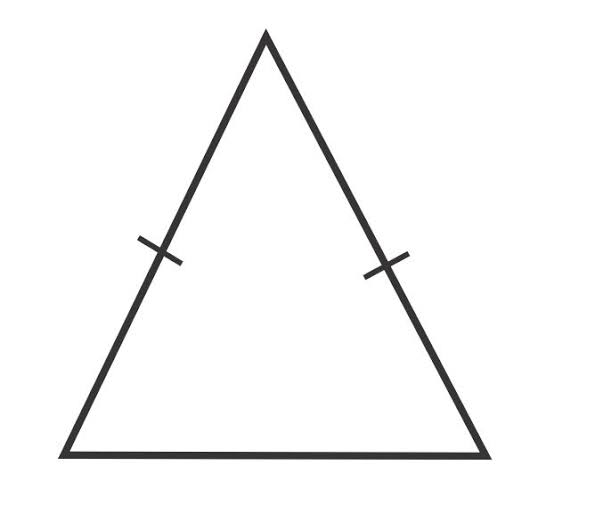
Angles in a Isosceles triangle

Angles opposite equal sides are equal

Reason: Angles opposite equal sides

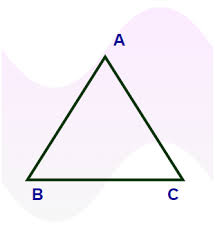
Given angle C = B, what can be said about the sides.

AB = AC

Reason: Sides opposite equal angles are equal.

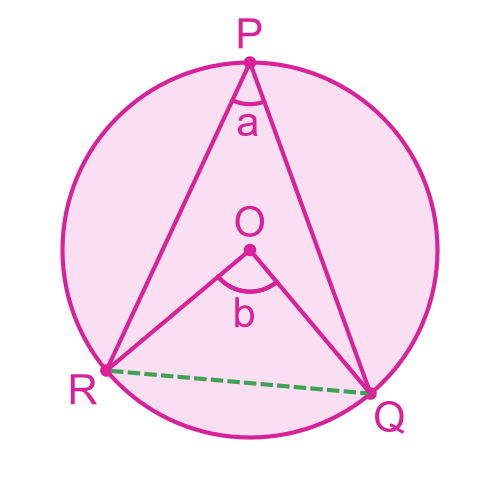
Central angle

The angle at the centre of a circle that subtends a chord.

Inscribed angle

An angle formed on the circumference by two chords, subtending a chord.

Chord

A line segment with both endpoints on the circle.

Diameter

A chord that passes through the centre; the longest chord.

Diameter = 2 x radius

Radius

A line segment from the centre of the circle to any point on the circle.

Tangent

A line that touches the circle at exactly one point.

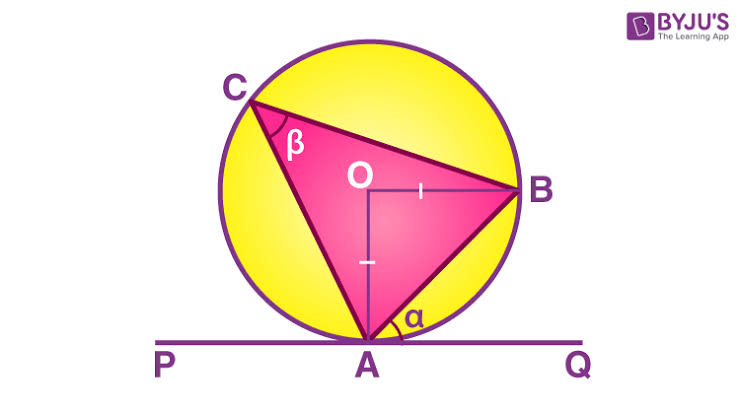
Tangent–radius perpendicularity

The radius to the point of tangency is perpendicular to the tangent.

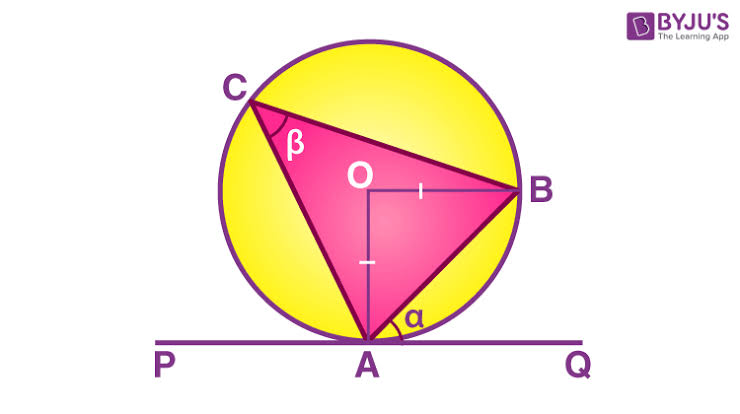
OA is a radius and PAQ is a tangent

PAQ = 90°

Reason: radius perpendicular to tangent

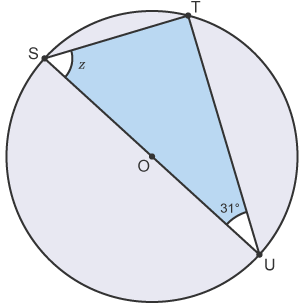
SOU is the diameter

Angle T =90°

Reason: Angle in a semicircle

Cyclic quadrilateral

A quadrilateral whose four vertices lie on a circle.

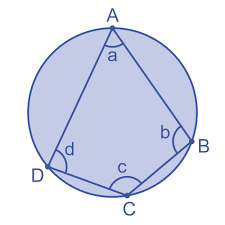
ABCD is a cyclic quadrilateral

a + c = 180

b + c = 180

Reason: Opposite angles are supplementary

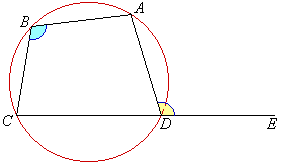
ABCD is a cyclic quadrilateral

ADE = b

Reason: external angle of cyclic quad

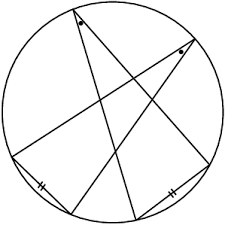
The chords are equal in the given image

The angles at the circumference are equal

Reason: Equal chords subtend equal angles

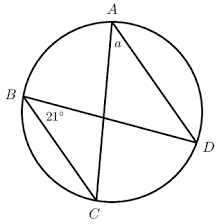
ABCD is a cyclic quad. What is a?

a = 21°

Reason: angles in same segment

Parallelogram Properties

Opposite sides are parallel and equal; opposite angles are equal; diagonals bisect each other.

Rhombus Properties

All sides are equal; opposite sides are parallel; opposite angles are equal.

Square Properties

All sides equal; diagonals bisect each other at 90° and bisect the corner angles; opposite sides are parallel; angles are 90°.

Rectangle Properties

Opposite sides are parallel and equal; diagonals bisect each other and are equal in length.

Kite Properties

Two pairs of adjacent sides are equal; diagonals intersect at 90°; one diagonal bisects the corner angles.

Trapezium Properties

One pair of opposite sides are parallel; one diagonal may bisect the corner angles (and diagonals may have other properties as noted).