Two Samples Independent/Unpaired Groups t-test for Continuous Data

When is the two sample (independent groups) t-test used?

To determine whether the unknown means of two populations are different from each other based on independent samples from each population

What can the samples for a two-sample t-test be obtained from?

• A single population that has been randomly divided into two subgroups, with each subgroup subjected to one of two treatments or

• From two separate populations (eg. Male and female)

• In either case, for the two-sample t-test to be valid, it is necessary that the two samples are independent (ie. Unrelated to each other)

What are the design condsiderations (assumptions) for two samples independent t-tests?

• Quantitative data must be continuous ratio/interval as means are compared

• The subjects are randomly selected from the same population or randomly selected from two separate populations

• Assumes normality

• Samples with equal variance

What are two-sample t-test hypotheses?

• Non-directional test = different

• Directional test = same

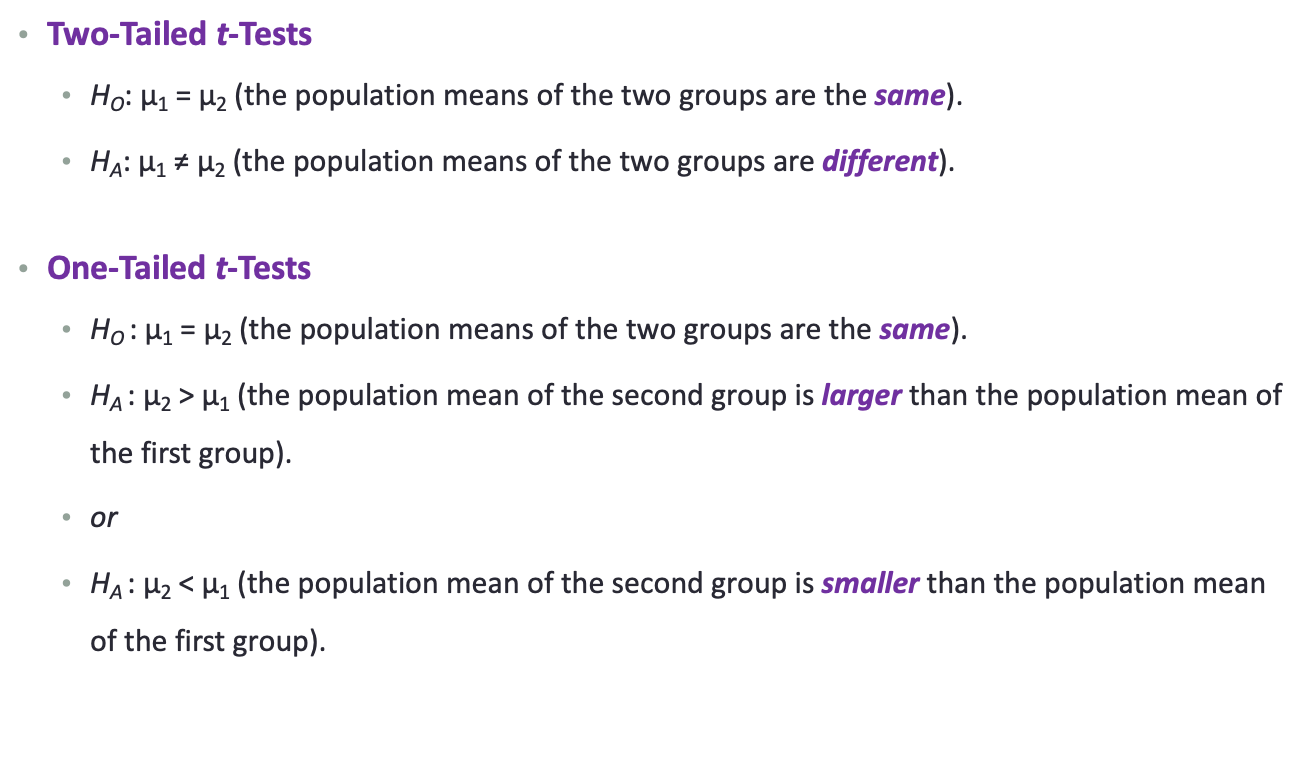
How do you report the results of an independent samples t-test?

Method:

• A two-sample independent (unpaired) student's t-test was performed to test the hypothesis that the mean number of days taken to recover from malaria with Drug A was the same as that for drug B

Results:

• The test of normality using Shapiro-Wilks statistic confirmed the data, recovery time in days for Drug A and Drug B has a normal distribution (W(8)=0.964, P=0.843, W(7)=0.953). Levene's Test for Equality of Variances (F=1.82, p=0.200) showed equal variances. An independent samples t-test indicated that the mean difference (3.38) between drug A (mean=23.38, SD=4.17, N=8) was not statistically different from that of Drug B (mean=20.0, SD=2.45, N=7), t(13)=1.87, p=0.084, using a two-sided test. Therefore, it can be concluded that there is no significant difference between Drug A and Drug B in recovery times

What happens when you test the hypothesis in one direction?

• For instance, we may have had prior knowledge that told us that we expect Drug A to be better treatment and so we expect Drug A to result in taking fewer days to recover from malaria

• Never just look at your dependent variable data and use these as evidence to carry out a one-tailed test, it simply increases the chance of you incorrectly rejecting the null hypothesis (type 1 error). A one tailed test needs to be planned in your research protocol

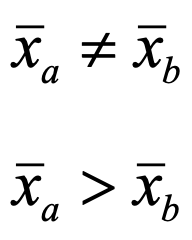
How do you perform a one tailed test for independent samples t-test?

• Simply read the significance value (p-value) for one-sided p from SPSS output (p=0.042)

• By using a one-side test, we now have evidence to reject the null hypothesis, since the p-value (0.042) is less than alpha 0.05

What are the two-sample t-test cautions?

• Don’t misuse the two-sample t-test such as: comparing paired subjects, comparing to a known value

• Preplan directional one-tailed t-tests with strong evidence

• Small sample sizes make normality difficult to assess (outliers can be a problem)

• Performing multiple t-tests causes loss of control of the experiment-wise significant level (ANOVA)