A&A SL: SL textbook: Bivariable Statistics

Chapter 19: SL textbook: Lessons A-C

Poles

Poles

• the highest and lowest data values

• Interpolating

  • when predicting that the x and y values would lie between the poles

  • the accuracy of the prediction is determined by the fit within the linear model

• Extrapolating

  • when predicting that the x and y values would lie outside of the poles

  • the accuracy of the prediction is determined by the linear fit and under the assumption that the trend will pass the poles

Line of Best Fit

• only worth drawing when there is a strong correlation between variables

• How to draw:

1. calculate the mean values of both x and y

2. mark the mean points

3. draw a line between the mean points which best fits the data so the points are equally distributed around the line

Line of Best Fit by Eye

• when drawing a line by observation

• will vary from person to person

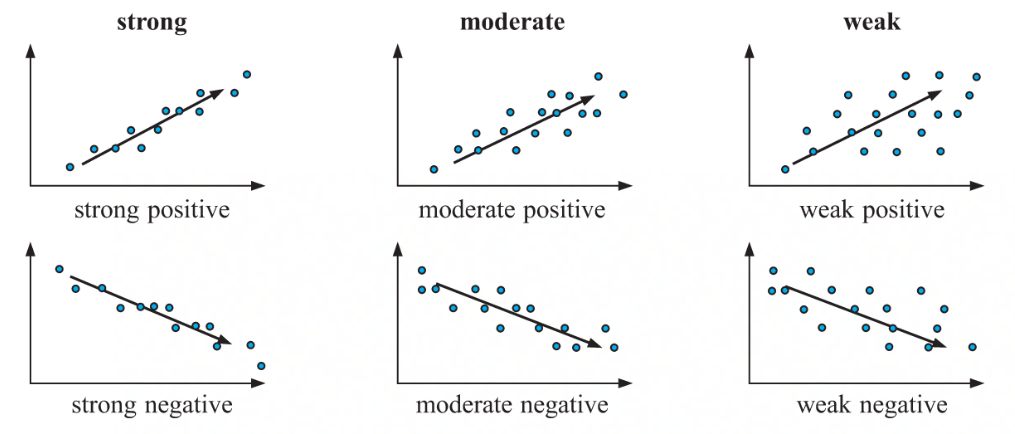
Correlations of r

• sign indication of r

  • when + r = positive correlation

  • when - r = negative correlation

  • when 0 = r = no correlation

• size indication of r

  • when r is close to + 1 or - 1 then there will be a strong correlation

  • when r is close to 0 then there will be a weak correlation

Pearson”s Product-moment Correlation Coefficient

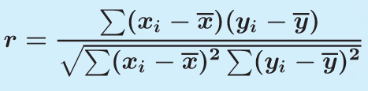
Causal Relationship

• AKA: explanatory variable/response variable

• if a change in one variable explains the change in the other variable

  • independent variable explains the dependent variable

• a causal relationship can not be determined based on high occurrence alone

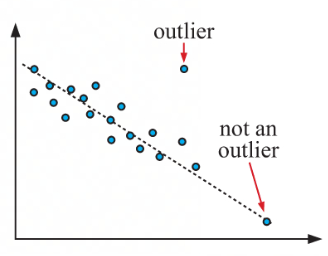
Outlier

• isolated points from the trend formed by the main data body

• discard if it is a result of a recording error

• keep if it is genuine data

Strength

• used to determine how closely a trend is followed

• correlation will be described as either:

  • strong

  • moderate

  • weak

• subjective way to determine data trends

Linear

• when a trend exists

• the points will form an approximately straight line

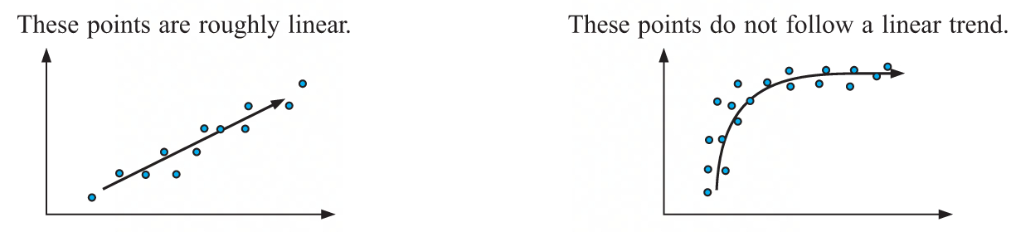
randomly scattered

• no correlation

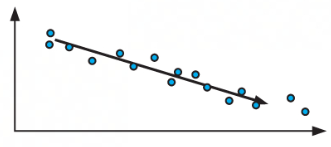
Downward Trend

• a negative correlation

• an increase in the independent variable

• a decrease in the dependent variable

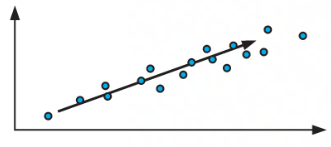
Upward Trend

• a positive correlation

• an increase in the independent variable

• an increase in the dependent variable

Correlation

• the relationship or association between two numerical values

• one variable does not inherently cause the other

Scatter Diagram

• shows the relationship between two numerical values

• the independent variable is on the horizontal axis

• the dependent variable is on the vertical axis