Graph Theory and Probability Flashcards

Vocabulary flashcards covering core concepts in graph theory, directed graphs, probability fundamentals, and basic set theory.

Complete Graph (K_n )

A graph with n vertices where every distinct pair of vertices is connected by an edge.

Path Graph (P_n)

path, line graph

Cycle Graph (C_n)

a graph which is a circle

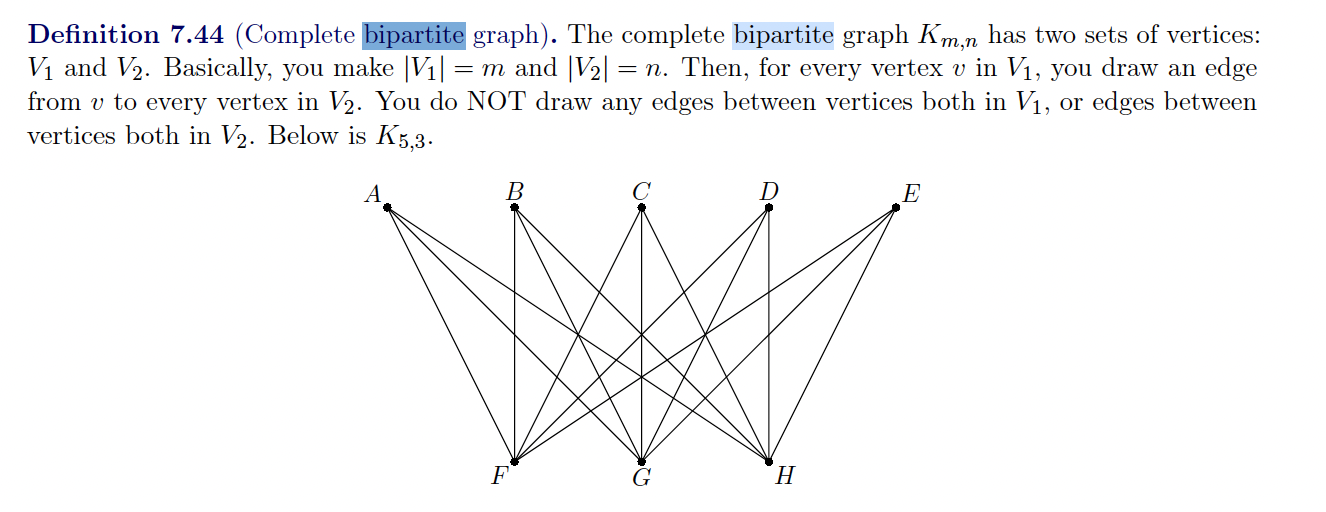
Bipartite Graph

A graph whose vertices can be divided into two disjoint sets, U and V, such that every edge connects a vertex in U to one in V.

Definition of a Tree

A connected acyclic graph.

Cut Edge

An edge whose removal increases the number of connected components.

Graph Coloring

Assigning colors to vertices so no adjacent vertices have the same color.

Chromatic Number (\chi(G) )

The MINIMUM number of colors needed for a proper coloring of G.

Independent Set

A set of vertices where no two vertices are adjacent.

Clique

A subset of vertices where every two distinct vertices are adjacent (i.e., a complete subgraph).

Strong Connectivity

For any two vertices u, v, there's a directed path from u to v AND from v to u.

Strongly Connected Component (SCC)

A maximal set of vertices in which every pair is mutually reachable.

Reduced Graph (Condensation Graph)

A DAG formed by contracting each SCC into a single vertex.

Directed Acyclic Graph (DAG)

A directed graph with no directed cycles.

Topological Sort

A linear ordering of DAG vertices such that for every edgeu \rightarrow v, u comes before v.

Probability Space (\Omega )

The set of all possible outcomes of an experiment.

Uniform Probability Space

All outcomes are equally likely. P(\omega) = 1/|\Omega| .

Event (in Probability)

A subset of the sample space \Omega .

Conditional Probability P(A|B)

"Probability of A given B": P(A|B) = \frac{P(A \cap B)}{P(B)}, if P(B) > 0.

Independent Events (A and B)

P(A \cap B) = P(A)P(B) . Equivalently: P(A|B)=P(A) if P(B)>0)

Power Set 2^A)

The set of all subsets of A.