calc final notecards

What is the average rate of change?

Slope of the secant line (passes through two points)

f(b)-f(a)/b-a

What is the instantaenous rate of change?

Can approximate the slope of the tan line (derivative at a point) with the slope of the secant line

(1) taking the derivative

(2) evaluating at x=a

(3) f’(a) !!

lim f(x)-f(a)/x-a

x → a

What are the rules of derivatives?

Power rule: nx^n-1

Limit definition of a derivative: f’(x) = f(x+h)-f(x)/h

For when you are given a point instead of an equation: f’(a) = f(x)-f(a)/x-a

Steps for taking a limit

(1) Substitution

(2) Expand factor

(3) Simplify

(4) Complex fraction

Rules for limits going to infinity (n/m)

n<m lim = 0

n=m ratio of the leading coefficients

n>m + or - inf based on the signs

*left and right hand limits have to be equal

To find limits at infinity

We take the closest number from each side and it’ll be + or - infinity depending on the sign

*remember to factor

How do we find vertical asymptotes?

(1) Set denominator to 0

(2) Check the limit approaching that number from both sides (keeping the range in mind) and there will be a vertical asymptote when the limit approaches pos or neg infinity

How do we find a horizontal asymptote?

(1) Identify the highest power

(2) Apply the n/m rule

• n<m y=0

• n=m ratio of the leading coefficients

• n>m ± inf

(3) Limit as the function approaches infinity (dividing each term by the highest degree term)

A function is continuous when

(1) f is defined at x=a (substitute the point)

(2) f has a limit as x → a (left side lim = right side lim)

(3) lim f(x) = f(a)

What are the different types of discontinuities?

(1) removable discontinuity (when there is a hole aka c/0)

(2) jump discontinuity (limits from left and right exist but are no equal)

(3) infinite discontinuity (approaches ± infinity aka a VA exists)

What is the IVT?

If a function is continuous on [a,b] and a y-value is between f(a) and f(b), then f(c)=0

• we can use this to show that there are roots by plugging in the endpoints and seeing if there is a change in sign => at least one root

How do we find the derivative at a point?

Would allow us to find the instantaneous rate of change at a given point/ slope of the tan line to the graph

lim f(a+h)-f(a)/h

h → 0

What is the limit definition of a derivative?

lim f(x+h)-f(x)/h

h → 0

What is the rule for the derivative of an exponential function?

f(x) = a^x

=> f’(x) = a^xlna

unless the base is e

What is the second derivative?

if f’(x) is increasing => f’’(x) is concave up

STEPS FOR INFLECTION POINTS

(1) f’’(a) = 0 (possible inflection)

(2) sign chart to check values on either side

(3) if concavity changes (a, f(a)) is an inflection point

What are the orders of the derivatives?

f(x) = position

f’(x) = velocity

f’’(x) = acceleration

how do we use local linearization?

approximating a curve from a line

STEPS:

(1) choose the appropriate function

(2) calculate f(a) and f’(a)

(3) L(x) = f(a)+f’(a)(x-a)

(4) ^^ plug in and find the linear approximation

What is the derivative of sin(x)?

cos(x)

What is the derivative of cos(x)?

-sin(x)

What is the derivative of -sin(x)?

-cos(x)

What is the derivative of -cos(x)?

sin(x)

What is the derivative of ln(x)?

ln(x) = 1/x

What is the derivative of e^x?

e^x

Pythagorean identity for trig

sin2(x)+cos2(x) = 1

csc(x)?

-cscx cot x

sec(x)?

secx tanx

cotx

-csc2x

What does the graph for e^x look like?

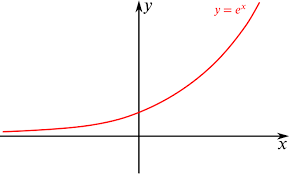
What does the graph for e^-x look like?

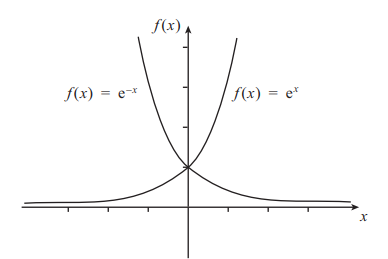
What does the graph of lnx look like?

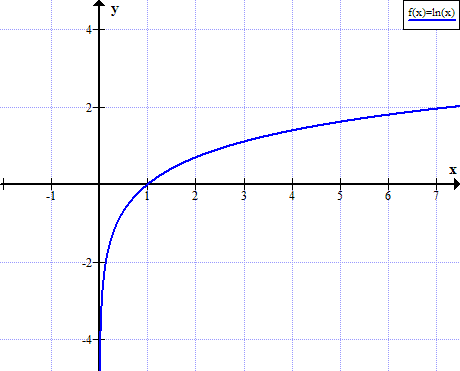
What are the equations for a circle that we should know?

D=2r

C=2pir

A=pir²

Perimeter = pir + 2r

Cylinder

V=bh

Trapezoid

1/2(b1+b2)h

What are the inverse trig derivatives?

(1) arcsin = 1/√1-x²

(2) arccos = -1/√1-x²

(3) arctan = 1/1+x²

The chain rule

derivative of the outside (og inside into the x value) times derivative of the inside

Steps for implicit differentiation

(1) differeniate both sides with respect to x

(2) treat both sides as a function of x

(3) use the chain rule when differentiating y terms (dy/dx)

How do we approach related rates?

(0) Draw a picture

(1) Label your picture with knowns, unknowns, constants, & write the values you want to find

(2) write an equation that relates this information

(3) take the derivative d/dt

(4) plug in and check

L’hopitals rule

Only when 0/0 or inf/inf

(1) Take the derivtive of the top and bottom separately

(2) Take the limit again

How to find the local extrema?

(1) Take the derivative

(2) Solve for f’(x) = 0 to find critical points

(3) First derivative test (change of the slope); + → — local max (plug into derivative)

(4) Second derivative test for the local min or max at a critical point

How to find global extrema?

(1) Take the derivative

(2) Find the critical points in (a,b)

(3) Evaluate the original function aka f(x)

(4) Compare the y-values

(5) Check the given endpoints

How do we sketch a curve?

1. Find the domain (denom doesn’t =0; all real numbers for polynomials)

2. Find the intercepts (y= when x=0; AND x= where y=0)

3. Find the first derivative

4. Find the critical points

5. Use the first derivative test

6. Use the second derivative test

7. Find inflection points

8. VA’s by seeing where the denominator is 0

9. HA’s by seeing where: n is less than m (0) OR n=m where y=leading coefficient number OR n>m no HA

Global Optimization steps

(1) Derivative

(2) Critical points in (a,b)

(3) Evaluate og function

(4) Compare y-values

(5) Check the given endpoints

What is the extreme value theorem?

If a function is continuous on [a,b] => has a global max and min on [a,b]

Applied optimization

(1) Identify the goal

(2) Draw a labeled picture, relate variables, identify domain

(3) Possible extrema (critical points/ endpoints); compare values if EVT applies

(4) Check reasonability

What is the mean value theorem?

If the function is continuous over [a,b] and differentiable over (a,b) => there is one point over (a.b) where

f’(c)=f(b)-f(a)/b-a

IV=Avg ROC

Antiderivatives

Written like: F(x)+C

What is Rolle’s Theorem?

If a function is continuous on [a.b], differentiable on (a,b), and f(a)=f(b)

=> f’(c) = 0 (there will be a horizontal tangent line between a and b)

How to use sigma notation

3

∑​(2k+1)

k=1

Step-by-step:

• When k = 1: 2(1)+1= 3

• When k = 2: 2(2)+1= 5

• When k = 3: 2(3)+1= 7

Add: 3+5+7=15

How to use sigma notation for Riemann Sums?

(1) Find delta x (b-a/n)

(2) xk​=a+kΔx so we basically are just adding the first term of the set to the delta x multiple by the k value (and the k value would just progressively increase)

(3) write it in :)

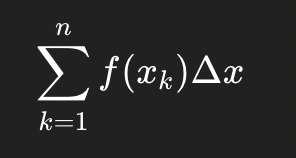
How to find right and left Riemann Sums?

A= delta x (f(2)+f(3)….)

left would just be n-1

How do we find midpoint riemann sums?

Basically the same idea, we just find the midpoint of each of the values we’re looking at in the interval

When are Riemann sums an underestimate and when are they an overestimate?

Left = underestimate when concave up

Right = overestimate when concave up

How do we use limits with Riemann sums?

(1) Find delta x

(2) xk = a+deltax times k

(3) plug into formula and foil out as needed

(4) Can move constants out and then apply the summation formula given to us

(5) Then its just a matter of simplifying

(6) Take limit like we would for other limits to infinity (dividing by the highest power term) => simplify

Definite integral form

a to b (bottom to top)\

if a < b - the net signed area

f is a rate = net change in x=a and x=b

also as a limit of riemann sums

How do we find the definite integral?

(1) Antiderivative

(2) Take the integral of the antiderivative by subtracting the two values F(b)-F(a)

Properties of integrals

• constants can be inside of outside

• smaller b value than a => negative

• same value = 0

• Adding and subtracting:

  essentially an integral is saying F(3) - F(2) so if we’re adding that to an integral that says F(5)-F(2) we’re subtracting F(5)-F(2)

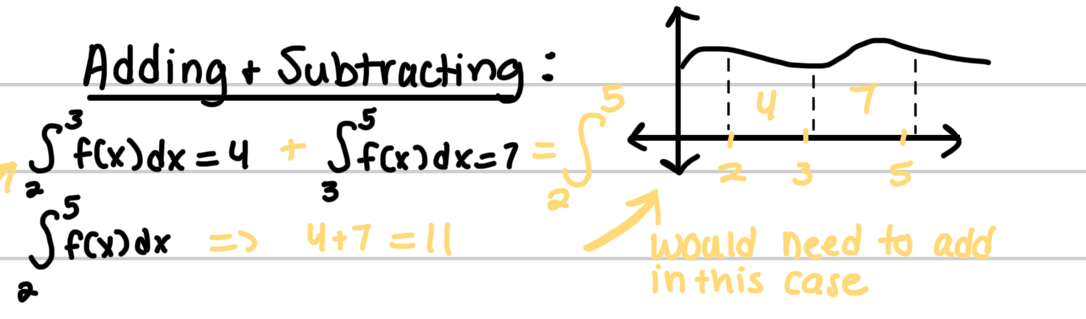
What is the fundamental theorem of calculus?

A continuous function on [a,b] and F(x) is an antiderivative => integrals are basicall F(b)-F(a)

We can calculate an integral by

(1) finding an antiderivativr

(2) F(b)-F(a)